Расчёт геометрических параметров зубчатых колёс

Коэффициент воспринимаемого смещения:

.

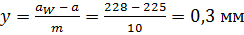Воспринимаемое смещение:

.

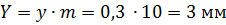Коэффициент уравнительного смещения:

.

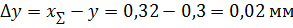Уравнительное смещение:

.

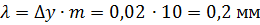Радиусы начальных окружностей:

;

.

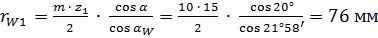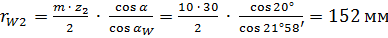Радиусы делительных окружностей:

;

.

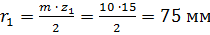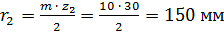Радиусы основных окружностей:

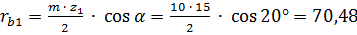мм ;

.

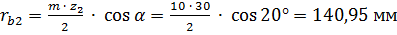Радиусы окружностей вершин:

;

.

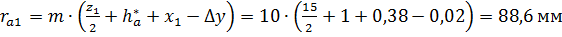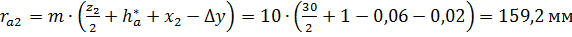Радиусы окружностей впадин:

;

.

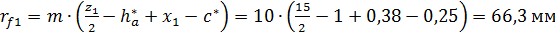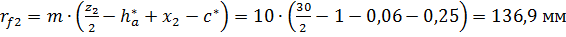Высота зубьев шестерни и колеса:

.

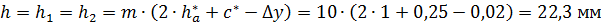Проверка:

;

;

;

.

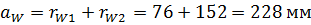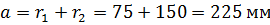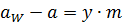
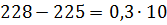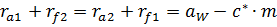
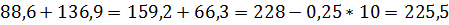Шаг окружной делительный:

.

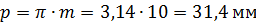Шаг окружной основной:

.

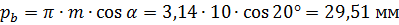Шаг по хордам делительных окружностей:

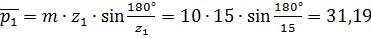мм ;

.

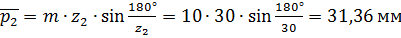Толщина зубьев окружная делительная:

;

.

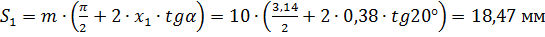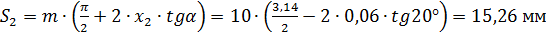Толщина зубьев по хордам делительных окружностей:

;

.

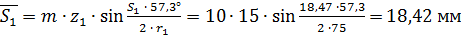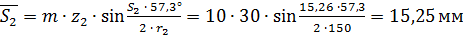Радиус кривизны активного профиля зуба в нижней точке:

а) для шестерни (точка 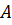или )

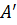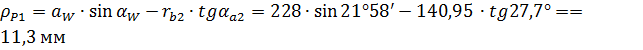, где

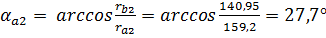- угол профиля зуба в точке на окружности вершин.

б) для колеса (точка 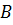или )

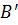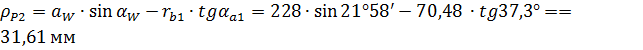, где

.

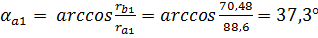Радиус кривизны профиля зуба в точке на окружности вершин:

а) для шестерни (точка 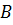или )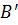

;

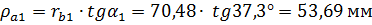б) для колеса (точка 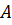или )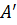

.

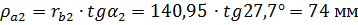Радиус кривизны профилей зубьев в точках на начальных окружностях:

а) для шестерни

;

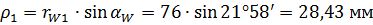б) для колеса

.

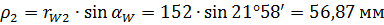Проверка:

;

;

;

.

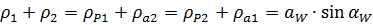
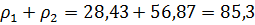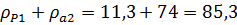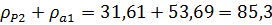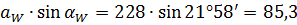Показатели качества зацепления и их проверка

1) Проверка отсутствия интерференции зубьев (заклинивания).

Радиус кривизны в граничной точке профиля зуба:

.

.

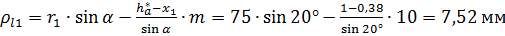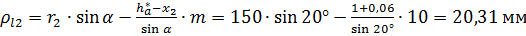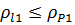
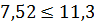
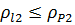
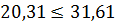
Вывод: интерференция зубьев отсутствует.

2) Проверка отсутствия подрезания зубьев.

Коэффициент наименьшего смещения:

;

.

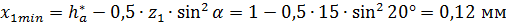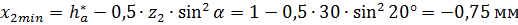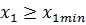
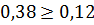
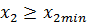
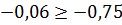
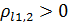
Вывод: подрезание зуба исходной производящей рейкой отсутствует.

3) Проверка коэффициента перекрытия передачи.

Коэффициент перекрытия:

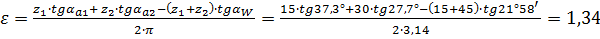
Для прямозубых передач рекомендуется .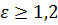

4) Проверка заострения зубьев.

;

.

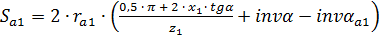
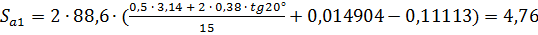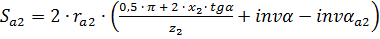
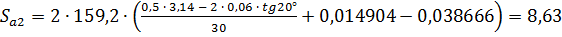При однородной структуре материала зубьев их заострение отсутствует, если 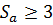, а при поверхностном упрочнении зубьев - .

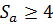5) Удельное скольжение в крайних точках активной линии зацепления.

В точке :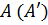

· на ножке зуба шестерни ;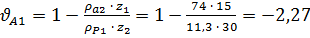

· на головке зуба колеса .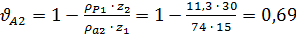

В точке :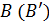

· на головке зуба шестерни ;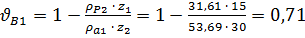

· на ножке зуба колеса .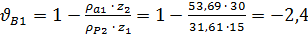

Контрольные размеры

1)Постоянная хорда зуба:

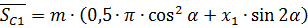
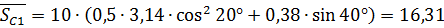мм ;

.

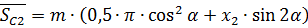
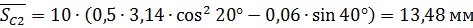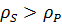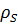Должно выполняться условие , где - радиус кривизны разноименных профилей зуба в точках, определяющих постоянную хорду.

;

.

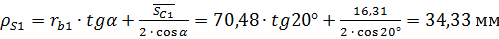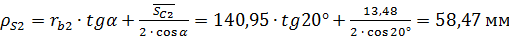2) Высота до постоянной хорды от окружности вершин:

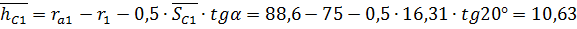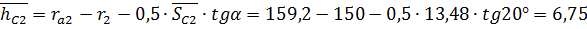мм ;

мм .

3) Длина общей нормали:

;

.

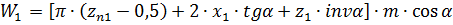
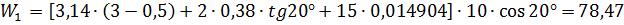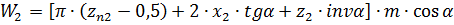
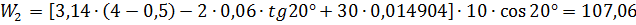Здесь 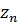– число зубьев в длине общей нормали;

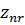– расчётное число зубьев в длине общей нормали, округляемое до ближайшего целого числа .

;

.

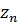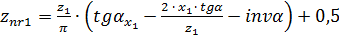
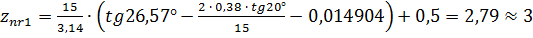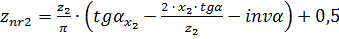
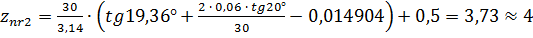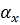– угол профиля зуба в точке на концентрической окружности радиуса .

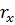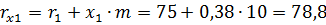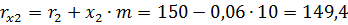мм ;

мм .

.

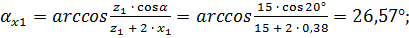
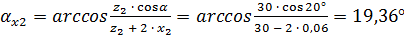Услови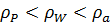е , где 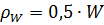, выполняется верно.

Заключение

В данном курсовом проекте мной был изучен плоский шарнирный механизм, для точки B были построены кинематические диаграммы, по которым видно как изменяются с течением времени перемещение, скорость и ускорение данной точки. Для первого положения механизма были построены планы скоростей и ускорений, из которых можно определить скорость и ускорение любой точки механизма в этом положении. Из силового анализа была выведена результирующая сила, действующая на стойку. Был произведён синтез зубчатой передачи, предназначенной для приведения шарнирного механизма в движение. Для оценки спроектированной зубчатой передачи были рассчитаны качественные показатели зацепления.

Литература:

1. Новиков В.Ф. и Квасов В.И. «Кинематическое исследование плоских шарнирных механизмов», 1977 г.

2. Красюков А.П. «Силовой расчёт плоских механизмов с низшими кинематическими парами», 1979 г.

3. Красюков А.П. «Проектирование зубчатого зацепления», 1978 г.