Применение теорем об эквивалентных бесконечно малых при вычислении пределов и таблицы эквивалентностей
Замена переменных при вычислении пределов, использование непрерывности функции при вычислении пределов.
а) Правило замены переменной для непрерывной функции.
По определению непрерывности функции в точке 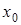 ,
, 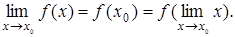
Если дана сложная функция 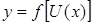 , функция
, функция 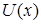 имеет предел в точке
имеет предел в точке 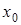 и функция
и функция 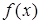 непрерывна в точке
непрерывна в точке 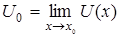 , то
, то
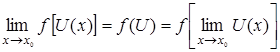 .
.
То есть при вычислении предела непрерывной функции можно перейти к пределу под знаком функции. Например, в силу непрерывности основных элементарных функций справедливы равенства:
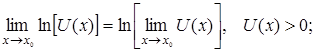
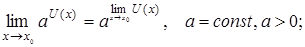
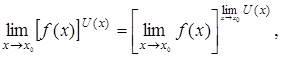 если
если 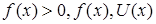 – непрерывные функции и т. д.
– непрерывные функции и т. д.
Пример 5. Вычислить 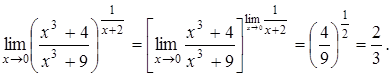
б) Правило замены переменной для пределов функций в общем виде.
Пусть существуют пределы 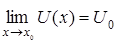 и
и 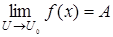 и
и 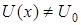 при
при 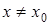 . Тогда при
. Тогда при 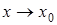 существует предел сложной функции
существует предел сложной функции 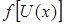 и
и 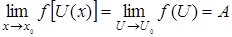 .
.
Это правило полезно при вычислении предела в том случае, когда 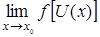 вычислить трудно. Полагают
вычислить трудно. Полагают 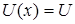 и находят предел
и находят предел 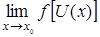 при условии, что этот предел вычисляется проще первоначального.
при условии, что этот предел вычисляется проще первоначального.
Пример 6. Вычислить 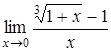 .
.
Решение. Сделаем замену переменной 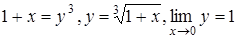 , тогда
, тогда
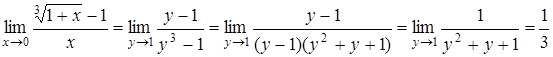 .
.
Применение замечательных пределов при вычислении пределов функций
Предел 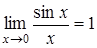 называется первым замечательным пределом (раскрывает неопределенность
называется первым замечательным пределом (раскрывает неопределенность 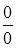 ).
).
Если функция 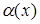 такова, что
такова, что 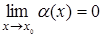 , то
, то 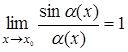 .Этот предел имеет важное значение при раскрытии неопределенности
.Этот предел имеет важное значение при раскрытии неопределенности 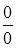 .
.
Пример 7. Вычислить
а) 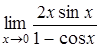 ; б)
; б) 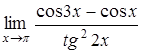 .
.
Решение. а) Имеем неопределенность 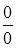 .
.
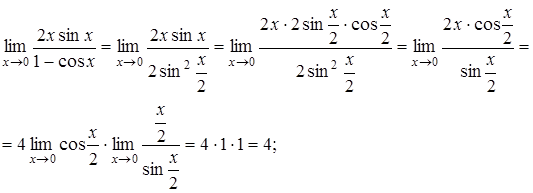
б) 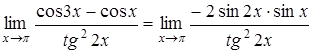 .
.
Так как 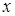 стремится не к 0, а к
стремится не к 0, а к 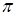 , то сделаем замену переменной
, то сделаем замену переменной 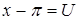 . При
. При 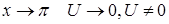 при
при 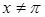 , а
, а 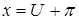 .
.
Имеем
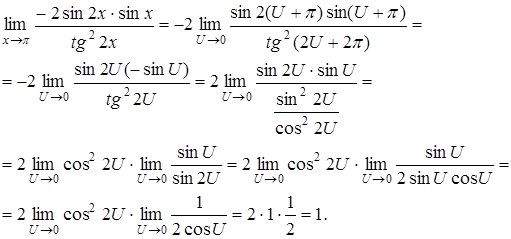
Второй замечательный предел имеет вид
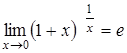
или
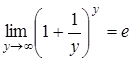 , где е=2,71826…– иррациональное и трансцендентное число. Если
, где е=2,71826…– иррациональное и трансцендентное число. Если 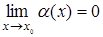 , то
, то 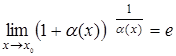 . Если
. Если 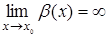 , то
, то 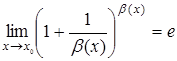 .
.
С помощью второго замечательного предела раскрывается неопределенность 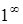 , то есть ищутся пределы показательно- степенных функций
, то есть ищутся пределы показательно- степенных функций 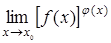 , где
, где 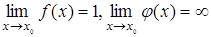 .
.
Предположим, что 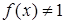 в окрестности точки
в окрестности точки 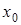 , за исключением, быть может, самой точки
, за исключением, быть может, самой точки 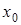 . Применяя формулу второго замечательного предела и возможность перехода к пределу отдельно в основании и показателе степени, получаем:
. Применяя формулу второго замечательного предела и возможность перехода к пределу отдельно в основании и показателе степени, получаем:
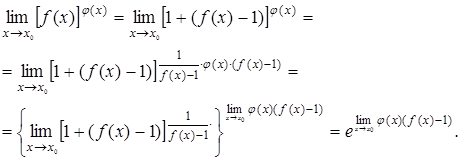
Пример 8. Вычислить 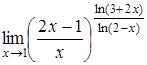 .
.
Решение.
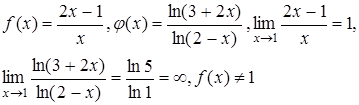
в окрестности 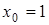 за исключением точки
за исключением точки 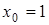 .
.
Применяя вышеуказанные преобразования, получим
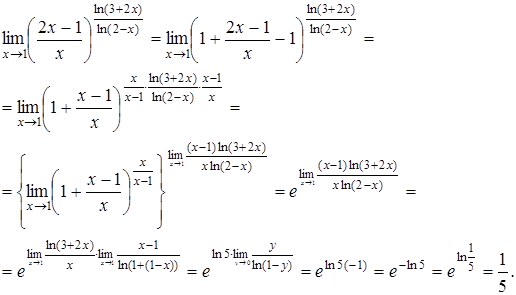
В процессе вычисления предела получили 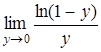
Вычисляем
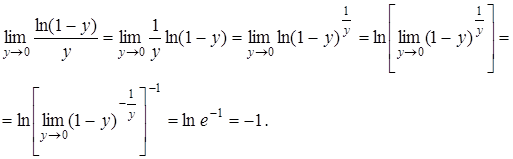
Следовательно, и 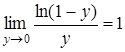 .
.
Ответ: 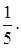
Пример 9.Вычислить 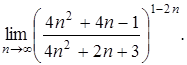
Решение. Имеем 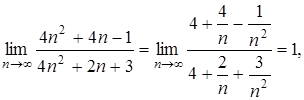
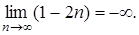
При вычислении этого предела аналогично используем второй замечательный предел
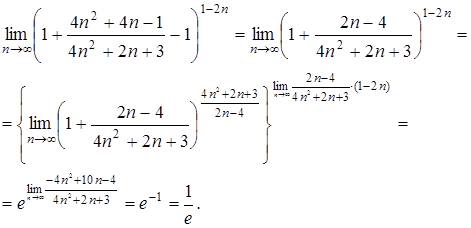
Применение теорем об эквивалентных бесконечно малых при вычислении пределов и таблицы эквивалентностей.
Пусть 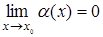 и
и 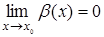 . Если
. Если 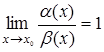 , то
, то 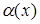 и
и 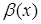 называются эквивалентными бесконечно малыми в точке
называются эквивалентными бесконечно малыми в точке 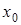 . Это обозначается как
. Это обозначается как 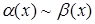 при
при 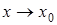 .
.
Теорема 1. Если 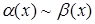 ,
, 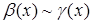 при
при 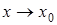 , то
, то 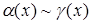 при
при 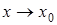 .
.
Теорема 2. Если 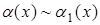 ,
, 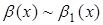 при
при 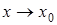 , то
, то 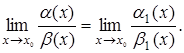
Теорема 3. Алгебраическая сумма конечного числа бесконечно малых эквивалентна бесконечно малой низшего порядка. Иначе: пусть 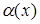 – бесконечно малая низшего порядка по сравнению с
– бесконечно малая низшего порядка по сравнению с 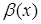 ,
, 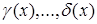 , тогда
, тогда 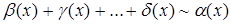 .
.
Теорема 4. Если 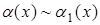 ,
, 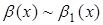 при
при 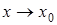 , причем
, причем 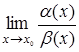 существует и отличен от –1, то
существует и отличен от –1, то 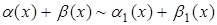 при
при 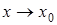 .
.
Таблица эквивалентностей.
Пусть 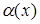 – бесконечно малая при
– бесконечно малая при 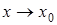 , то есть
, то есть 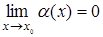 . Тогда
. Тогда
1. 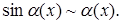
2. 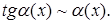
3. 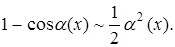
4. 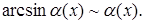
5. 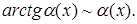
6. 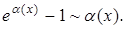
7. 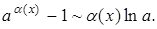
8. 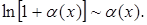
9. 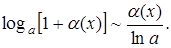
10. 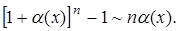
11. 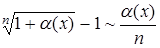 .
.
Все приведенные выше формулы справедливы при 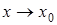 . Рассмотрим примеры на вычисление пределов с помощью теорем об эквивалентных бесконечно малых и таблицы эквивалентностей.
. Рассмотрим примеры на вычисление пределов с помощью теорем об эквивалентных бесконечно малых и таблицы эквивалентностей.
Пример 10. Вычислить
а) 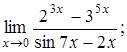 б)
б) 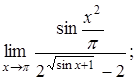 в)
в) 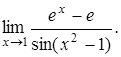
Решение.
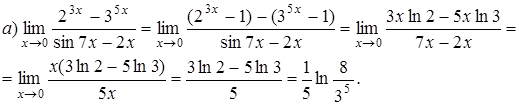
При вычислении этого предела применили теоремы 2 и 5 и табличные эквивалентности 1) и 7).
б) Имеем неопределенность 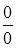 .
.
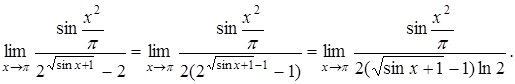
Применим эквивалентность 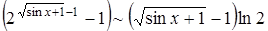 , так как
, так как 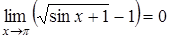 . Но нельзя считать, что
. Но нельзя считать, что 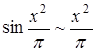 , поскольку
, поскольку 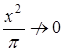 при
при 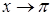 . Поэтому сделаем замену переменной
. Поэтому сделаем замену переменной 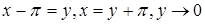 при
при 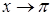 . Тогда имеем:
. Тогда имеем:
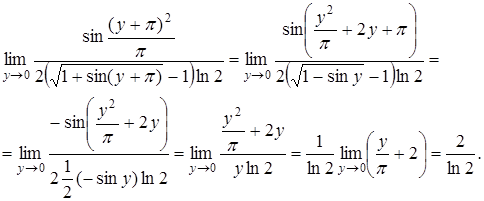
Использовали формулы приведения 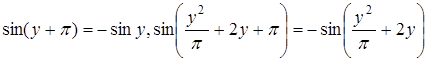 , табличные эквивалентности 1) и 11) и теорему 1:
, табличные эквивалентности 1) и 11) и теорему 1: 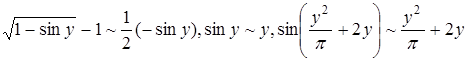 , так как
, так как 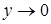 .
.
в) В данном случае также имеем неопределенность 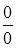 .
.
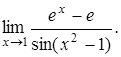
Сделаем замену 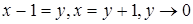 при
при 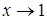 .
.
Получаем
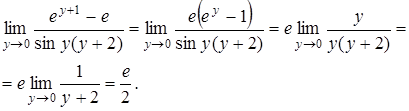
Применили эквивалентности 1) и 6).
Ответ: а) 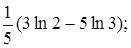 б)
б) 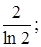 в)
в) 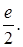
Пример 11. Вычислить 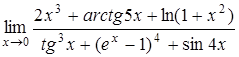 .
.
Решение. Так как при 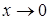
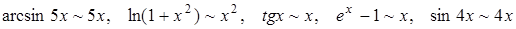 , то
, то
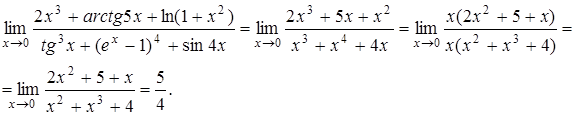
Ответ: