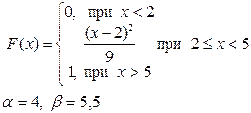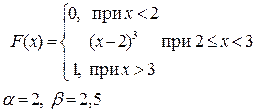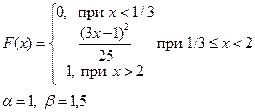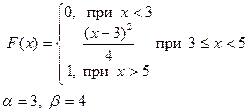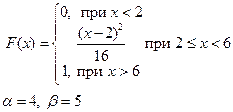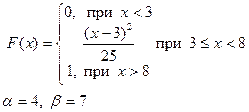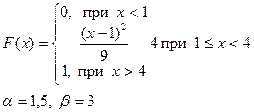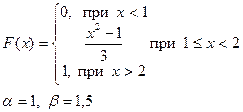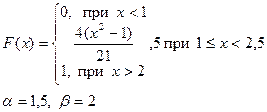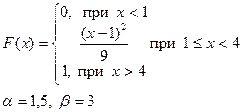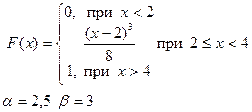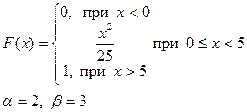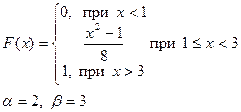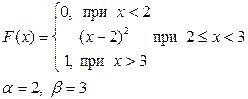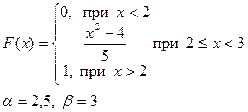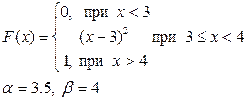Приклад розв’язку завдання 2

Елементи теорії ймовірності І

МАТЕМАТИЧНОЇ СТАТИСТИКИ»

з дисципліни «ВИЩА МАТЕМАТИКА»

З прикладами розв’язання типового варіанту

(для студентів 2 курсу денної форми навчання

за напрямом підготовки 6.080101 – «Геодезія, картографія та землеустрій»)

Відповідає вимогам кредитно-модульної системи організації навчального процесу

Харків – ХНУМГ – 2013

Завдання для самостійної роботи за темою «Елементи теорії ймовірності» з дисципліни «Вища математика» з прикладами розв’язання типового варіанту (для студентів 2 курсу денної форми навчання за напрямом підготовки 6.080101 – «Геодезія, картографія та землеустрій»). / Укл.: Данилевський М.П., Мордовцев С.М.. – Харків: ХНУМГ, 2013. – 40 с.

Укладачі: М.П. Данилевський,

С.М. Мордовцев

Завдання для самостійної роботи побудовано за вимогами кредитно-модульної системи організації навчального процесу та узгоджена з орієнтовною структурою змісту навчальної дисципліни, рекомендованою Європейською Кредитно-Трансферною Системою (ЕСТS).

Рекомендовано для студентів, що навчаються за напрямом підготовки 6.080101 – «Геодезія, картографія та землеустрій»).

Рецензент: зав. кафедри вищої математики Харківської національного університету міського господарства ім. О.Б. Бекетова, доктор фізико-математичних наук, проф. Колосов А.І.

Затверджено на засіданні кафедри вищої математики.

протокол №3 від 24.10.2012 р.

© Данилевський М.П., Мордовцев С.М., ХНУМГ, 2013

Завдання 1

Закон розподілу випадкової величини x заданий таблицею (перша строчка – можливі значення x, друга – відповідні їм значення ймовірностей p). Знайти: а) математичне очікування;

б) дисперсію;

в) середнє квадратичне відхилення випадкової величини x;

г) побудувати графік інтегральної функції розподілу F(X) .

	xi
pi	0,1	0,24	0,31	0,2	0,15
	xi
pi	0,04	0,15	0,24	0,3	0,27
	xi
pi	0,05	0,18	0,4	0,22	0,15
	xi
pi	0,1	0,2	0,35	0,2	0,15
	xi
pi	0,03	0,14	0,25	0,36	0,22
	xi
pi	0,1	0,24	0,31	0,2	0,15
	xi
pi	0,04	0,15	0,24	0,3	0,27
	xi
pi	0,1	0,2	0,35	0,2	0,15
	xi
pi	0,03	0,14	0,25	0,36	0,22
	xi
pi	0,12	0,24	0,4	0,14	0,1
	xi
pi	0,08	0,2	0,3	0,22	0,2
	xi
pi	0,1	0,24	0,31	0,2	0,15
	xi
pi	0,05	0,12	0,4	0,25	0,18

Продовження табл.

	xi
pi	0,1	0,24	0,31	0,2	0,15
	xi
pi	0,02	0,14	0,4	0,26	0,18
	xi
pi	0,13	0,27	0,34	0,23	0,03
	xi
pi	0,07	0,18	0,27	0,33	0,15
	xi
pi	0,08	0,21	0,43	0,25	0,03
	xi
pi	0,08	0,18	0,33	0,18	0,23
	xi
pi	0,03	0,14	0,25	0,36	0,22
	xi
pi	0,08	0,22	0,37	0,18	0,15
	xi
pi	0,1	0,21	0,3	0,36	0,03
	xi
pi	0,16	0,2	0,35	0,26	0,03
	xi
pi	0,05	0,15	0,3	0,36	0,14
	xi
pi	0,1	0,24	0,42	0,14	0,1
	xi
pi	0,06	0,22	0,32	0,22	0,18
	xi
pi	0,07	0,21	0,35	0,17	0,2
	xi
pi	0,1	0,15	0,35	0,22	0,18
	xi
pi	0,12	0,24	0,4	0,18	0,06
	xi
pi	0,05	0,14	0,41	0,26	0,14

Приклад розв’язку завдання 1

xi
pi	0,1	0,15	0,35	0,25	0,15

З аналізу ряду розподілу обчислимо математичне сподівання:

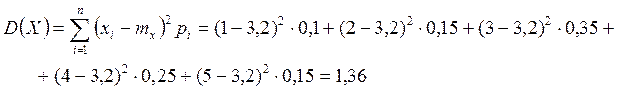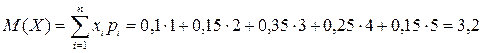
дисперсію і середнє квадратичне відхилення:

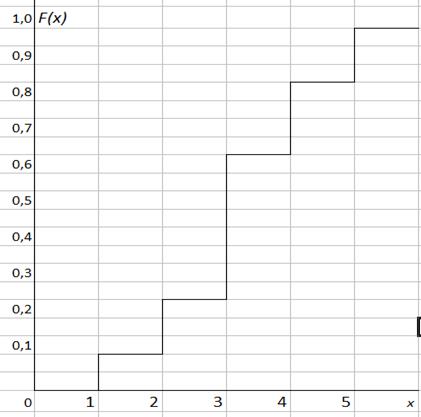Рис. 1.1 – Графік інтегральної функції розподілу F(X)

Завдання 2

Випадкова величина x задана інтегральною функцією розподілу F(x). Знайти:

а) диференціальну функцію (щільність ймовірностей) розподілу;

б) математичне очікування, дисперсію, середнє квадратичне відхилення;

в) побудувати графік інтегральної та диференціальної функції;

г) обчислити ймовірність попадання випадкової величини в інтервал (α,β).

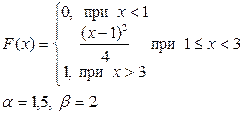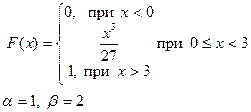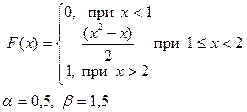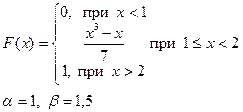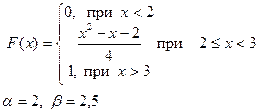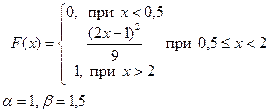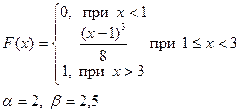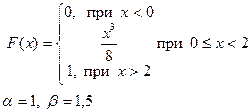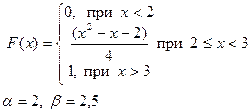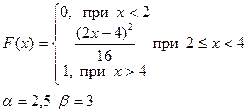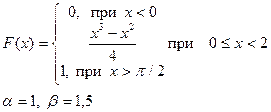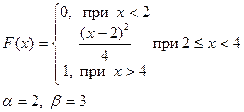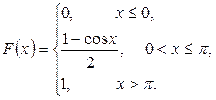Приклад розв’язку завдання 2

Випадкова величина x задана інтегральною функцією розподілу F(x).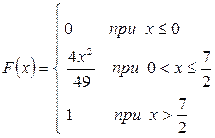

а) Знайдемо диференціальну функцію (щільність ймовірностей) розподілу:

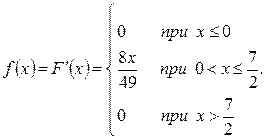
б) Обчислимо математичне очікування, дисперсію, середнє квадратичне відхилення:

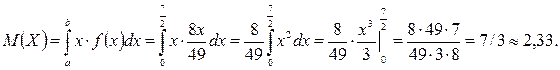
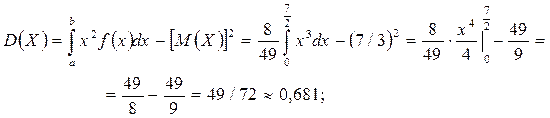
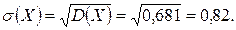
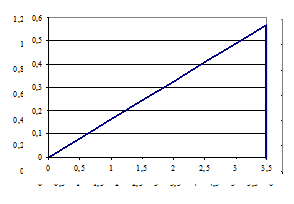Рис. 2.1– Графік інтегральної функції F(X)

Рис. 2.1– Графік диференціальної функції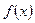

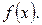
Завдання 3

За вибіркою, що наведено у таблиці, необхідно згідно з варіантами:

а) знайти рівняння лінійної регресії та побудувати графіки точкової функції і регресійної прямої;

б) підрахувати коефіцієнти кореляції і детермінації;

в) оцінити значущість рівняння регресії, використовуючи критерій Фішера;

г) оцінити значущість коефіцієнтів рівняння регресії, використовуючи t-критерій Ст’юдента, і визначити довірчий інтервал для кожного коефіцієнта рівняння регресії.

Варіанти
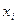				12,5	1,1
1,5	8,2			9,7	1,6
	6,5				2,2
2,5	4,8				3,2
	3,6			5,5	4,1
3,5	2,8			4,8	5,5
	2,1		-2	4,2	7,3
4,5	1,7		-9	3,5	10,5
	1,6	-2	-14
5,5	1,3	-6	-19	2,5	16,1
Варіанти
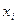	11,5	13,2	2,2	11,7	19,3
	7,7	10,4	2,7	7,4	18,8
		7,7	3,3	6,1	17,4
	4,3	6,7	4,3	4,2	13,6
	3,1	6,2	5,2	3,5	9,1
	2,3	5,5	6,6	2,5	4,3
	1,6	4,9	8,4	1,7
	1,2	4,2	11,6	1,2	-5
	1,1	3,7	15,1	1,1	-13
	0,8	3,2	17,2	0,8	-20

Продовження табл.

Варіанти
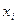	10,2	10,9	1,3	-1,8
1,5			1,7	-1,3	19,5
	6,6	7,7	2,3	-0,7	18,3
2,5		6,7	3,1	0,3	16,5
	5,1	5,5		1,2
3,5	4,5	4,8	5,4	2,6
	3,8	4,1	7,2	4,4	-1
4,5		3,6	10,4	7,6	-8
	2,6	3,2	14,1	11,1	-14
5,5	2,2	3,1		13,2	-20
Варіанти
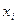		5,6	17,1	-6,9	11,8
	3,9		13,3	-6,4	9,7
	2,2	6,6	11,6	-5,8	8,3
	0,5	7,4	9,9	-4,8	7,5
	-0,7	8,3	8,7	-3,9	6,6
	-1,5	9,7	7,9	-2,5
	-2,2	11,5	7,2	-0,7	5,4
	-2,6	14,7	6,8	2,5	4,6
	-2,8	17,5	6,7		4,2
	-3		6,4	8,1
Варіанти
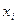	16,4		8,4	15,2	5,4
1,5	15,4	5,5	4,1	12,4	1,6
	14,4	6,1	2,8	9,7	-0,1
2,5	13,4	7,1	0,9	8,7	-1,8
	10,4		0,2	8,2	-3
3,5	6,4	9,4	-0,8	7,5	-3,8
		11,2	-1,6	6,9	-4,5
4,5	-2	14,4	-2,1	6,2	-4,9
	-6,1	17,9	-2,2	5,7	-5
5,5	-10		-2,5	5,2	-5,3

Продовження табл.

Варіанти
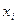	7,8	-4,3		4,7	18,1
		-3,8		5,2	14,3
	2,3	-3,2		5,8	12,6
	1,3	-2,2		6,8	10,9
	0,8	-1,3		7,7	9,7
	0,1	0,1		9,1	8,9
	-0,5	1,9	-2,4	10,9	8,2
	-1,2	5,1	-7,4	14,1	7,8
	-1,7	8,6	-11,5	17,6	7,7
	-2,2	10,7	-15,4	19,7	7,4