Уравнение с разделяющимися переменными.Билет 2

Определение 7.

ОДУ 1-ого порядка с разделяющимися переменными называется уравнение вида 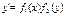или в дифференциальной форме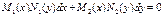

Теорема 1.

Если в уравнении 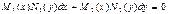функции 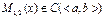, , 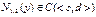причём в прямоугольнике 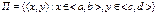функции ,

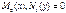то 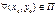задача Коши

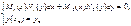(3)

имеет решение и притом единственное.

Заметим, что в случае, если 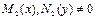, то уравнение 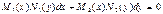переписывается в виде:

.

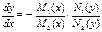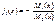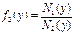Если теперь ввести обозначения и ,тоуравнение переписывается в виде 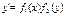, и задача (3) приобретает стандартный вид задачи Коши (2).

Доказательство.

ЭТАП (нахождение общего решения уравнения)

Перепишем уравнение 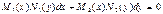в виде:

, (*)

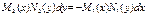идалее воспользуемся условием 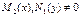, которое позволит нам поделить последнее равенство на 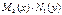. Получим:

. (**)

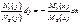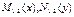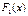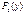Поскольку, по условию, все функции непрерывны, а функции, стоящие в знаменателях еще и отличны от нуля, то существуют первообразные и функци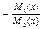й и 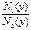, соответственно. Для них равенство (**) переписывается так:

(***)

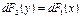Но если равны дифференциалы функций, то сами функции могут отличаться только на константу, то есть

(!)

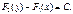Равенство (!) представляет собой запись общего решения исходного уравнения 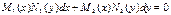, а равенство 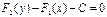– запись его общего интеграла.

ЭТАП (нахождение решения задачи Коши)

Поскольку все решения нашего уравнения могут быть записаны в виде (!), то и частное решение, которое удовлетворяет условию Коши 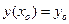, если оно существует, должно, при некотором значении константы 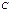иметь тот же вид (!). Чтобы найти подходящее значение 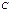, подставим в (!) условие Коши. Получим:

. (!!)

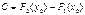Тут важно заметить, что каково бы ни было начальное условие, т.е. 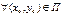, константа 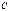, удовлетворяющая (!!), всегда существует и притом определяется единственным образом. Поэтому существует и притом единственное решение исходной задачи Коши (3), и оно задается формулой

.

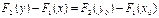Замечание.

В уравнении (*) как в левой, так и в правой частях есть функции, зависящие от 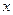, и функции, зависящие от 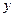. В то же время при переходе к (**) мы добились, чтобы в левой части встречалась только переменная 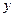, а в правой – только 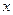. Этот процесс носит название разделения переменных.

Пример.

Решить уравнение с разделяющимися переменными 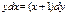. Для разделения переменных обе части уравнения разделим на 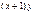. Чтобы не потерять решение, необходимо проверить, являются ли корни 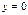, 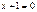решениями исходного уравнения. Для этого рассмотрим 3 случая:

1) 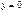, т.е. 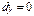, подставляем в исходное уравнение и получаем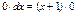 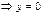решение.

2) 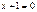, , 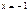т.е. 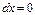, подставляем в исходное уравнение и получаем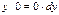 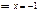решение.

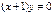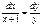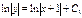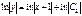3) , тогда , или , где 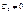. Потенцируя уравнение, получаем: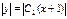 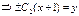, , 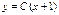где .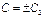

Запишем: 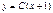, , 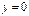, 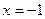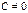. Т.к. решение 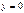получается из решения 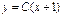при 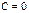, то допустив, что 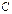может принимать значение, равное нулю, получаем окончательно: 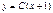, , 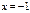где - любое.

Билет

Функция 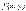называется однородной функцией степени 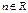, если 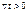справедливо .

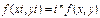Определение 0.2.

Однородным уравнением называется уравнение вида 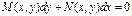, где 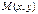, 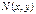- однородные функции одной и той же степени.

Определение 0.3.

Однородным уравнением называется ОДУ 1-ого порядка 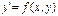, правая часть которого является однородной функцией нулевой степени, т.е. .

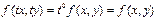Последнее равенство означает, что если точка 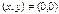принадлежит области определения функции 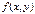, то этой же области принадлежит и открытый луч, проходящий через начальную точку и данную точку : .

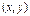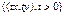Полагая 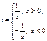, запишем .

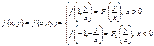В результате приходим ещё к одному определению однородного уравнения.

Определение 8.

Однородным уравнением называется уравнение вида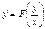

Теорема 2.

Если , ,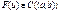

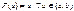то для любых 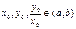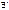решение задачи Коши

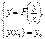(6)

Доказательство.

Введём новую неизвестную функцию 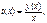тогда 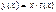, , 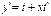, , 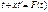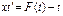при этом 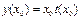. Задача Коши (6) сводится к следующей задаче 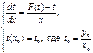. Получили задачу Коши для ОДУ 1-ого порядка с разделяющимися переменными. Согласно теореме (§3 настоящей главы) эта задача имеет решение и притом единственное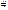

Пример.

Решить задачу Коши .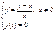

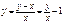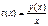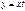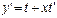
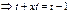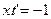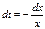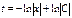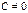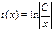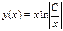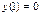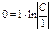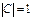Уравнение является однородным. Вводим новую неизвестную функцию , , , отсюда , , , где . , отсюда . Решаем задачу Коши: т.к. , то , ,т.е. 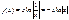.