Дифференциальное уравнение теплопроводности

В учебниках по теплопередаче, в том числе и в [1], приводится вывод дифференциального уравнения температурного поля движущейся жидкости, уравнение энергии

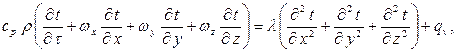(1.12)

где с_р, Дж/(кг×К) – изобарная теплоемкость; r, кг/м³ – плотность; l, Вт/(м×К) – коэффициент теплопроводности; w_х, w_y, w_z – проекции вектора скорости движения жидкости; q_v , Вт/м³ – объемная плотность внутреннего тепловыделения жидкости.

Уравнение (1.12) записано для случая l=const.

Дифференциальное уравнение температурного поля для твердых тел называется дифференциальным уравнением теплопроводности и может быть получено из (1.12) при условии w_х= w_y= w_z=0, с_р= с_v=с:

,

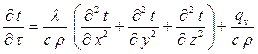где 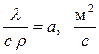- коэффициент температуропроводности, характеризует скорость изменения температуры в теле. Значения а = f (t) для различных тел приводятся в справочниках.

Дифференциальное уравнение теплопроводности

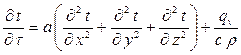(1.13)

описывает нестационарное температурное поле твердых тел с внутренним тепловыделением (с внутренними источниками тепла). Такими источниками тепла могут быть: джоулева теплота, выделяемая при прохождении электрического тока по проводникам; теплота, выделяемая ТВЭЛами ядерных реакторов и т.д.

Дифференциальное уравнение теплопроводности (1.13), записанное в декартовых координатах, можно представить в цилиндрических (r, z, φ) и сферических (r, φ, ψ).

В частности, в цилиндрических координатах (r –радиус; φ – полярный угол; z - аппликата) дифференциальное уравнение теплопроводности имеет вид

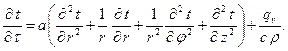(1.14)

Условия однозначности

Дифференциальное уравнение описывает множество процессов теплопроводности. Чтобы выделить из этого множества конкретный процесс, необходимо сформулировать особенности этого процесса, которые называются условиями однозначности и включают в себя:

· геометрические условия, характеризующие форму и размеры тела;

· физические условия, характеризующие свойства участвующих в теплообмене тел;

· граничные условия, характеризующие условия протекания процесса на границе тела;

· начальные условия, характеризующие начальное состояние системы при нестационарных процессах.

При решении задач теплопроводности различают:

· граничные условия первого рода, когда задается распределение температуры на поверхности тела:

t_c = f (x, y, z, τ) или t_c =const;

· граничные условия второго рода, когда задается плотность теплового потока на поверхности тела:

q_c = f (x, y, z, τ) или q_c =const;

· граничные условия третьего рода, когда задается температура среды t_ж и коэффициент теплоотдачи между поверхностью и средой.

В соответствии с законом Ньютона-Рихмана тепловой поток, передаваемый с 1м² поверхности в среду с температурой t_ж,

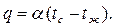
В то же время этот тепловой поток подводится к 1м² поверхности из глубинных слоев тела теплопроводностью

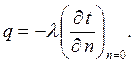
Тогда уравнение теплового баланса для поверхности тела запишется в виде

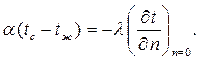(1.15)

Уравнение (1.15) является математической формулировкой граничных условий третьего рода.

Система дифференциальных уравнений совместно с условиями однозначности представляет собой математическую формулировку задачи. Решения дифференциальных уравнений содержат константы интегрирования, которые определяются с помощью условий однозначности.

Контрольные вопросы и задания

1. Проанализируйте, какими способами передается теплота от горячей воды к воздуху через стенку батареи отопления: от воды к внутренней поверхности, через стенку, от наружной поверхности к воздуху.

2. Почему в правой части уравнения (1.3) стоит минус?

3. Проанализируйте с помощью справочной литературы зависимость λ(t) для металлов, сплавов, теплоизоляционных материалов, газов, жидкостей и ответьте на вопрос: как изменяется коэффициент теплопроводности с изменением температуры для этих материалов?

4. Как определяется тепловой поток (Q, Вт) при конвективной теплоотдаче, теплопроводности, тепловом излучении?

5. Запишите дифференциальное уравнение теплопроводности в декартовых координатах, описывающее трехмерное стационарное температурное поле без внутренних источников теплоты.

6. Запишите дифференциальное уравнение температурного поля проволоки, которая длительное время находится под напряжением при постоянной электрической нагрузке.

2. ТЕПЛОПРОВОДНОСТЬ И ТЕПЛОПЕРЕДАЧА
ПРИ СТАЦИОНАРНОМ РЕЖИМЕ

2.1. Теплопроводность плоской стенки
при граничных условиях первого рода

Дано:плоская однородная стенка толщиной δ (рис. 2.1) с постоянным коэффициентом теплопроводности λ и постоянными температурами t₁ и t₂ на поверхностях.

Определить:уравнение температурного поля t=f (x) и плотность теплового потока q, Вт/м².

Температурное поле стенки описывается дифференциальным уравнением теплопроводности (1.3) при следующих условиях:

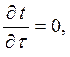· т. к. режим стационарный;

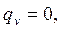· т.к. отсутствуют внутренние источники теплоты;

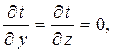· т.к. температуры t₁ и t₂ на поверхностях стенки постоянны.

Температура стенки является функцией только одной координаты х и уравнение (1.13) принимает вид

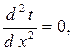(2.1)

т.к. коэффициент температуропроводности стенки а ≠ 0.

Граничные условия первого рода:

при х=0 t= t1 ,	(2.2)
при х= δ t= t2.	(2.3)

Выражения (2.1), (2.2), (2.3) являются математической постановкой задачи, решение которой позволит получить искомое уравнение температурного поля t= f (x).

Интегрирование уравнения (2.1) дает

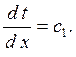
При повторном интегрировании получим решение дифференциального уравнения в виде

t=с1х+с2.

(2.4)

Из уравнения (2.4) при условии (2.2) получим

t₁=с₂,

а при условии (2.3)

t₂=с₁ δ + t₁ ,

откуда

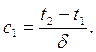
Подстановка констант интегрирования с₁ и с₂ в уравнение (2.4) дает уравнение температурного поля

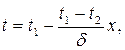(2.5)

по которому можно рассчитать температуру по толщине стенки на любой координате 0<x<δ.

Зависимость t= f (x), согласно (2.5) – прямая линия (рис. 2.1), что справедливо при λ=const.

Для определения плотности теплового потока, проходящего через стенку, воспользуемся законом Фурье

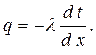
С учетом 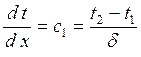получим расчетную формулу для плотности теплового потока, передаваемого через плоскую стенку,

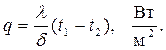(2.6)

Поток теплоты, передаваемый через поверхность стенки площадью F, вычисляется по формуле

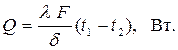(2.7)

Формулу (2.6) можно записать в виде

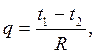
где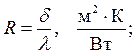

Величина 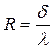называется термическим сопротивлением теплопроводности плоской стенки.

На основании уравнения

q R=t₁ – t₂

можно сделать вывод о том, что термическое сопротивление стенки прямо пропорционально перепаду температур по толщине стенки.

Учесть зависимость коэффициента теплопроводности от температуры, λ(t), можно, если в уравнения (2.6) и (2.7) подставить значения λ_ср для интервала температур t₁ –t₂.

Рассмотрим теплопроводность многослойной плоской стенки, состоящей, например, из трех слоев
(рис. 2.2).

Дано:δ₁ , δ₂ , δ₃, λ₁, λ₂, λ₃, t₁=const, t₄=const.

Определить: q, Вт/м²; t₂, t₃.

При стационарном режиме и постоянных температурах поверхностей стенки тепловой поток, передаваемый через трехслойную стенку, можно представить системой уравнений:

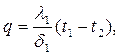	(2.8)
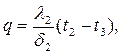	(2.9)
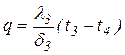	(2.10)

или

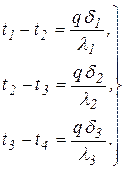(2.11)

Сложив левые и правые части уравнений (2.11), получим расчетную формулу для плотности теплового потока, передаваемого через трехслойную стенку

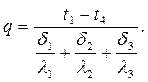(2.12)

Температуры на границах слоев t₂ и t₃ можно рассчитать по уравнениям (2.8) – (2.10) после того, как найдена плотность теплового потока (q) по (2.12).

Общий вид уравнения (2.12) для многослойной плоской стенки, состоящей из п однородных слоев с постоянными температурами на наружных поверхностях 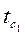и 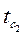, имеет вид

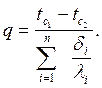(2.13)

Средний коэффициент теплопроводности многослойной стенки называют эффективным (λ_эф). Он равен коэффициенту теплопроводности однородной стенки, толщина и термическое сопротивление которой равны толщине и термическому сопротивлению многослойной стенки

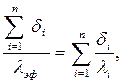
откуда

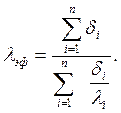(2.14)

2.2. Теплопроводность цилиндрической стенки
при граничных условиях первого рода

Дано:Однородная цилиндрическая стенка (стенка трубы) с внутренним радиусом r₁, наружным – r₂, длиной 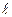, с постоянным коэффициентом теплопроводности λ, с постоянными температурами на поверхностях t₁ и t₂.
(рис. 2.3).

Определить: уравнение температурного поля
t = f (r), тепловой поток, передаваемый через стенку
Q, Вт.

Дифференциальное уравнение теплопроводности в цилиндрических координатах (1.14) для условий данной задачи:

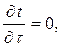
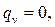
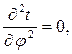
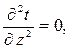
принимает вид

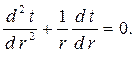(2.15)

Граничные условия первого рода:

при r=r1 t=t1 ,	(2.16)
при r=r2 t=t2 .	(2.17)

Порядок решения системы уравнений (2.15) – (2.17) тот же, что и в случае плоской стенки: находится общий интеграл дифференциального уравнения второго порядка (2.15), который содержит две константы интегрирования
с₁ и с₂ . Последние определяются с помощью граничных условий (2.16) и (2.17) и после подстановки их значений в решение дифференциального уравнения (общий интеграл) получаем уравнение температурного поля цилиндрической стенки t = f (r) в виде

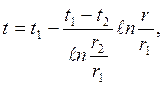(2.18)

где r₁ 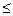r 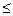r₂ – текущий радиус.

Нетрудно убедиться, что при подстановке в (2.18) r= r₁ получим t=t₁ , при r=r₂ получим t=t₂. Распределение температуры по толщине цилиндрической стенки, в соответствии с (2.18) подчиняется логарифмическому закону (рис. 2.3).

Для определения теплового потока воспользуемся законом Фурье:

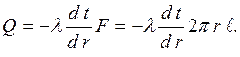(2.19)

Если взять производную 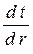от правой части уравнения (2.18) и подставить в (2.19), получим расчетную формулу для теплового потока цилиндрической стенки

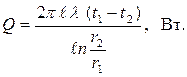(2.20)

В технических расчетах часто тепловой поток вычисляется для 1 м длины трубы:

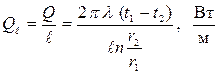
и называется линейной плотностью теплового потока.

Запишем уравнение (2.20) в виде

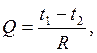
где 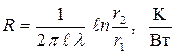– термическое сопротивление теплопроводности цилиндрической стенки.

Для трехслойной цилиндрической стенки (трубы, покрытой двумя слоями тепловой изоляции) с известными постоянными температурами поверхностей (t₁ и t₄), с известными геометрическими размерами (r₁ , r₂, r₃, r₄ , 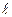) и коэффициентами теплопроводности слоев (λ₁, λ₂, λ₃) (рис. 2.4) можно записать следующие уравнения для теплового потока Q:

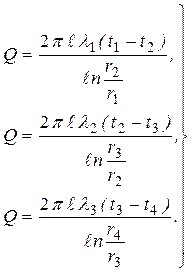(2.21)

Совместное решение системы уравнений (2.21) дает расчетную формулу для теплового потока, передаваемого через трехслойную стенку при заданных температурах на поверхностях,

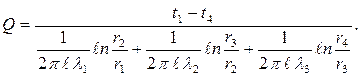(2.22)

Температуры на границах слоев (t₂, t₃) можно рассчитать по уравнениям (2.21).

Для многослойной цилиндрической стенки, состоящей из п слоев, формулу (2.22) можно записать в общем виде

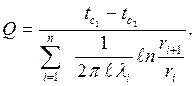(2.23)

Эффективный коэффициент теплопроводности для многослойной цилиндрической стенки, как и для многослойной плоской стенки, определяется из равенства суммы термических сопротивлений многослойной стенки термическому сопротивлению однородной стенки той же толщины, что и многослойная. Так, для двухслойной тепловой изоляции трубы
(рис. 2.4) эффективный коэффициент теплопроводности (λ_эф) определ ится из равенства

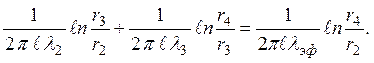
2.3. Теплопроводность плоской и цилиндрической стенок
при граничных условиях третьего рода (теплопередача)

Граничные условия третьего рода состоят в задании температуры жидкости (t_ж) и коэффициента теплоотдачи ( 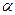) между поверхностью стенки и жидкостью.

Передача тепла от одной жидкости к другой через разделяющую их стенку называется теплопередачей.

Примерами теплопередачи служит перенос теплоты от дымовых газов к воде через стенку трубы парового котла, перенос тепла от горячей воды к окружающему воздуху через стенку батареи отопления и т.д.

Теплообмен между поверхностью и средой (теплоносителем) может быть конвективным, если теплоноситель – жидкость (вода, нефть и т.д.) или радиационно-конвективным, когда теплота передается путем конвективного теплообмена и излучением, если теплоноситель – газ (дымовые газы, воздух и т.д.).

Рассмотрим теплопередачу через плоскую и цилиндрическую стенки при условии только конвективного теплообмена на поверхностях. Теплопередача с радиационно-конвективным теплообменом (сложным теплообменом) на поверхностях будет рассмотрена позже.

Плоская стенка(рис. 2.5)

Дано:

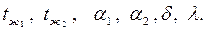
Определить: q, t₁, t₂.

Плотность теплового потока q описывается следующими уравнениями в зависимости от способа передачи теплоты:

– от горячей жидкости к стенке

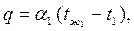(2.24)

– через стенку

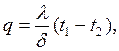(2.25)

– от стенки к холодной жидкости

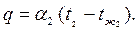(2.26)

Записав уравнения (2.24) – (2.26) в виде

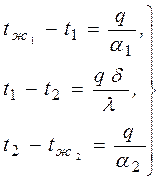(2.27)

и сложив почленно правые и левые части уравнений (2.27), получим формулу для расчета теплопередачи (q, Вт/м²) через плоскую стенку в виде

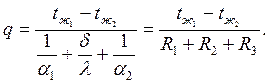(2.28)

Величины 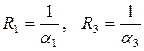называются термическими сопротивлениями теплоотдачи. Они прямо пропорциональны перепадам температур .

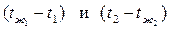Температуры на поверхностях стенки t₁ и t₂ можно рассчитать по уравнениям (2.24) – (2.26) после того, как определена плотность теплового потока (q) по уравнению (2.28).

Формулу (2.28) можно записать в виде

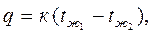(2.29)

где 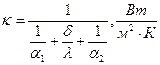- коэффициент теплопередачи плоской стенки,характеризует интенсивность процесса теплопередачи.

Теплопередача через многослойную плоскую стенку рассчитывается по формуле

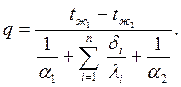(2.30)

Цилиндрическая стенка(рис. 2.6)

Дано:

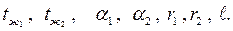
Определить: Q, Вт; t₁ , t₂.

Для цилиндрической стенки, по аналогии с плоской стенкой, можно записать следующую систему уравнений:

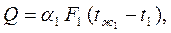	(2.31)
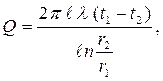	(2.32)
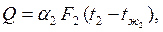	(2.33)

где 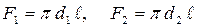- площади внутренней и наружной поверхностей трубы.

Записав уравнения (2.31) – (2.33) относительно разностей температур, а затем сложив правые и левые части уравнений, получим формулу для расчета теплопередачи (Q, Вт) через цилиндрическую стенку в виде

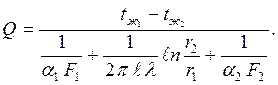(2.34)

Температуры на поверхностях стенки t₁ и t₂ рассчитываются по уравнениям (2.31) – (2.33).

Формулу (2.34) также можно представить в виде

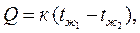
где 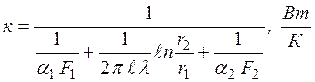– коэффициент теплопередачи цилиндрической стенки.

Для металлических труб с 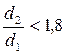можно пренебречь кривизной стенки и теплопередачу рассчитать по формулам для плоской стенки:

,

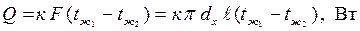где

.

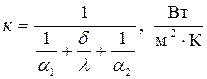Диаметр d_x=d₁ , если a₁<<a₂ ;

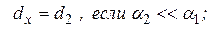
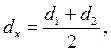если a₁ и a₂ соизмеримы.

Теплопередача через многослойную цилиндрическую стенку рассчитывается по формуле

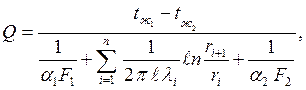(2.35)

где F₁ и F₂ – площади внутренней и наружной поверхностей многослойной цилиндрической стенки.