Регрессионный анализ. Проверка адекватности эмпирической модели по критерию Фишера
Регрессионный анализ
|
|
|
функция является регрессионной (корреляционной), если каждому
значению аргумента соответствует статистический ряд распределения у.
|
|
|
|
Чтобы предварительно определить наличие такой связи между и , наносят
|
|
измерения на рис. 1-б такой связи не показывают.
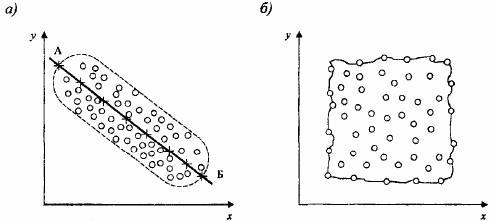 Рис. 1. Корреляционное поле
Рис. 1. Корреляционное поле
Различают однофакторные (парные) и многофакторные регрессионные зависимости. Парная регрессия при парной зависимости может быть аппроксимирована прямой линией, параболой, гиперболой, логарифмической, степенной или показательной функцией, полиномом и др. Двухфакторное поле можно аппроксимировать плоскостью, параболоидом второго порядка, гиперболоидом.

| |
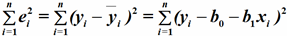

|
равенство её частных производных по неизвестным параметрам b0и 1.
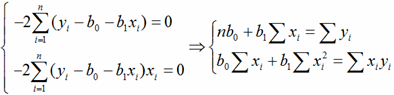
Разрешая аналитически данную систему уравнений, получаем:
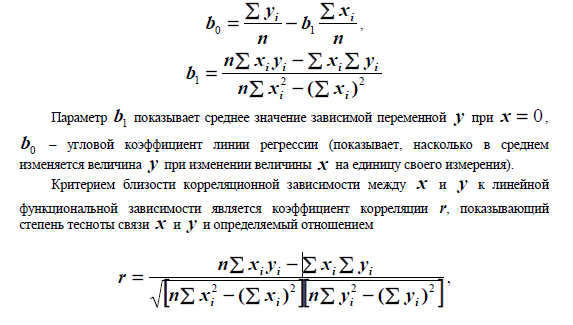
где n– число измерений.
-1£ r £1
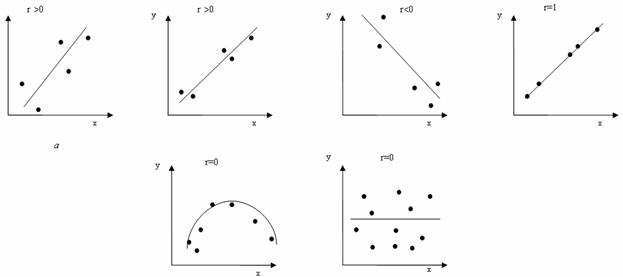
Коэффициент корреляции интерпретируется как мера линейной зависимости
случайных величин. При r > 0 между x и y существует положительная линейная
связь. При r < 0 между x и y существует отрицательная линейная связь. При r = 0
|
|
На рис. 2 представлены примеры меры линейной зависимости случайных величин и , линиями изображены прямые уравнения регрессии.
Проверка адекватности уравнения регрессии.
Надо убедиться, что полученное уравнение с достаточной степенью достоверности, адекватно описывает исследуемый процесс. Иными словами, необходимо убедиться, соразмерны ли степень воспроизводимости процесса со степенью адекватности уравнения процессу, т.е. сравнить среднюю дисперсию адекватности воспроизводимости среднего в каждой строчке результата с дисперсией адекватности.
Эта проверка осуществляется по F – критерию Фишера:
1.Рассчитывают выход 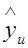 для каждого варианта опыта по уравнению регрессии, из которого исключены незначимые члены;
для каждого варианта опыта по уравнению регрессии, из которого исключены незначимые члены;
2.Находят разность 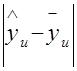 ;
;
3.Рассчитывают дисперсию адекватности
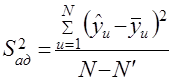 (3.27)
(3.27)
где 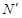 - число значимых коэффициентов в уравнении регрессии.
- число значимых коэффициентов в уравнении регрессии.
Эта разность 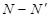 является числом степеней свободы, т.к. из N уравнений мы определили лишь
является числом степеней свободы, т.к. из N уравнений мы определили лишь 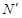 коэффициентов (а могли бы определить N коэффициентов).
коэффициентов (а могли бы определить N коэффициентов).
1.Рассчитывают критерий Фишера по формуле:
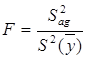 (3.28)
(3.28)
2.Сравнивают полученное значение критерия Фишера с его табличным значением FT (Приложение Б).
В таблицах критерий Фишера дан в зависимости от числа степеней свободы 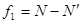 при определении дисперсии адекватности и
при определении дисперсии адекватности и 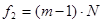 при определении средней дисперсии воспроизводимости единичного измерения, S2(yk), равного числу степеней свободы при определении средней дисперсии воспроизводимости среднего
при определении средней дисперсии воспроизводимости единичного измерения, S2(yk), равного числу степеней свободы при определении средней дисперсии воспроизводимости среднего 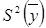 .
.
Критерий Фишера всегда больше единицы. Поэтому, в зависимости (3.28) в числитель поставлена дисперсия адекватности чисто условно. Если средняя дисперсия воспроизводимости 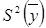 больше
больше 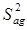 , то в числителе должна стоять
, то в числителе должна стоять 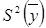 .
.
Промежуточные расчеты удобно представить в виде табл.3.7. 
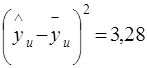
Дисперсия адекватности
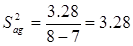 , т.к. N = 8, а
, т.к. N = 8, а 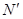 =7.
=7.
Так как 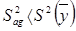 , то критерий Фишера имеете величину
, то критерий Фишера имеете величину
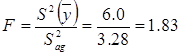
Таблица 3.7.Промежуточные расчёты по проверке адекватности
| u | 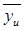 | 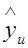 | 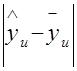 | 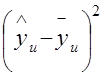 |
| 69,5 | 0,5 | 0,25 | ||
| 59,5 | 0,5 | 0,25 | ||
| 55,7 | 0,7 | 0,49 | ||
| 90,9 | 0,9 | 0,81 | ||
| 104,5 | 0,5 | 0,25 | ||
| 94,5 | 0,5 | 0,25 | ||
| 80,7 | 0,7 | 0,49 | ||
| 100,7 | 0,7 | 0,49 |
при f1 = 16 и f2 = 1 табличное значение критерия Фишера по Приложению Б равно FT » 8,65.
Сравнение табличного значения критерия Фишера FT с рассчитанным F удовлетворяет неравенству F < FT. На этом основании делается вывод об адекватности полученного уравнения регрессии исследуемому процессу. Следовательно, это уравнение может служить основой для отыскания оптимальных условий ведения процесса
36. Теорема Букингема. Уменьшение размерности и снижение плотности плана эксперимента
Для правильного применения анализа размерностей по Шенку [8] исследователь должен знать характер и число фундаментальных переменных в его эксперименте. Фундаментальной переменной называют любую величину, оказывающую влияние на эксперимент и способную изменять независимо от других переменных. Фундаментальные переменные необходимо отличать от регулируемых переменных. Например, ускорение силы тяжести можно изменить независимо от других переменных, рассматриваемых при проведении эксперимента, отправив аппаратуру на Луну, однако мы представляем себе, что в обычных лабораторных экспериментах это сделать невозможно.
Если экспериментатору действительно известны все переменные, то он может сразу же преобразовать их, применив первую часть теоремы Букингема: «Если какое-либо уравнение однородно относительно размерностей, то его можно преобразовать к соотношению, содержащему набор безразмерных комбинаций величин».
Однородным относительно размерностей является уравнение, форма которого не зависит от выбора основных единиц. Примером является известное уравнение Фэннинга для коэффициента трения 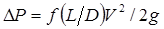 . Входящие в него величины могут выражаться в футах и секундах, метрах и часах или в любых других соразмерных единицах. И наоборот, уравнение Дюлонга и Пти
. Входящие в него величины могут выражаться в футах и секундах, метрах и часах или в любых других соразмерных единицах. И наоборот, уравнение Дюлонга и Пти 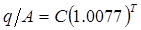 для теплового потока через единицу площади
для теплового потока через единицу площади 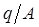 от источника, имеющего температуру
от источника, имеющего температуру 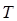 , не является однородным, так как, выражая
, не является однородным, так как, выражая 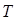 в градусах Кельвина, получим совсем другую формулу, чем при использовании
в градусах Кельвина, получим совсем другую формулу, чем при использовании 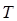 в градусах Ренкина. Правильная формула для этого случая была найдена позже. Она имеет вид
в градусах Ренкина. Правильная формула для этого случая была найдена позже. Она имеет вид 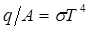 , где
, где 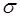 - некоторый размерный коэффициент. Действительно, сомнительно, чтобы какое-либо естественное явление можно было описать с помощью неоднородного уравне-ния. Такое описание может быть лишь приближенным.
- некоторый размерный коэффициент. Действительно, сомнительно, чтобы какое-либо естественное явление можно было описать с помощью неоднородного уравне-ния. Такое описание может быть лишь приближенным.
Безразмерные комбинации, о которых упоминалось в теореме Букинге-ма, представляют собой произведения или отношения величин, составленные таким образом, что в каждой комбинации размерности сокращаются. В случае уравнения Фэннинга можно составить три безразмерные комбинации: 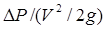 ,
, 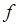 и
и 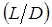 . теорема Букингема не является столь тривиальной, как это может показаться при рассмотрении этого простого примера, и её до-казательство довольно сложно.
. теорема Букингема не является столь тривиальной, как это может показаться при рассмотрении этого простого примера, и её до-казательство довольно сложно.
Выше отмечалось, что неоднородные уравнения не могут дать полного математического описания естественного явления или процесса. Можно не знать всех переменных, влияющих на эксперимент, но необходимо представ-лять себе, что эти переменные и связывающее их безразмерное уравнение существуют независимо от того, известны они или нет. Если не удается полу-чить систему безразмерных комбинаций, то это является верным признаком
того, что было что-то пропущено.
В случае уравнения Фэннинга для коэффициента трения в его наиболее общем виде обычно представляет интерес величина 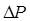 . Известно, что эта величина зависит от длины трубы
. Известно, что эта величина зависит от длины трубы 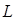 , диаметра
, диаметра 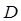 и скорости потока
и скорости потока 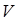 . Все эти величины являются независимыми переменными. Хотя ускорение силы тяжести
. Все эти величины являются независимыми переменными. Хотя ускорение силы тяжести 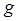 практически величина постоянная, его также необходимо рассмат-ривать. Легко убедиться, что такие свойства жидкости, как плотность и вязкость, являются независимыми переменными (зависящими от вида жидкости и ее температуры). Изучение внутренних поверхностей различных труб показывает, что высота неровностей поверхности
практически величина постоянная, его также необходимо рассмат-ривать. Легко убедиться, что такие свойства жидкости, как плотность и вязкость, являются независимыми переменными (зависящими от вида жидкости и ее температуры). Изучение внутренних поверхностей различных труб показывает, что высота неровностей поверхности 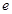 также является переменной величиной. Итак, получаем восемь фундаментальных переменных и общее уравнение можно записать в следующем виде:
также является переменной величиной. Итак, получаем восемь фундаментальных переменных и общее уравнение можно записать в следующем виде:
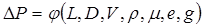 . (4.1.)
. (4.1.)
Согласно теореме Букингема, это функциональное соотношение (если оно однородно) можно выразить через безразмерные комбинации величин. Из опыта известно, что такое соотношение имеет следующий вид:
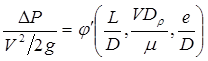 . (4.2)
. (4.2)
Можно показать, что эти комбинации являются безразмерными, если используются совместимые единицы. Экспериментатору значительно легче найти функцию 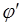 в формуле (4.2), чем функцию
в формуле (4.2), чем функцию 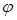 в формуле (4.1). Вместо того чтобы варьировать поочередно каждую из семи переменных, причем изменение некоторых из них может вызывать затруднения, исследователь может варьировать лишь каждую из трех комбинаций. Это обстоятельство существенно упрощает эксперимент и позволяет представить в графической форме и проанализировать полученные данные гораздо быстрее и с большей точностью.
в формуле (4.1). Вместо того чтобы варьировать поочередно каждую из семи переменных, причем изменение некоторых из них может вызывать затруднения, исследователь может варьировать лишь каждую из трех комбинаций. Это обстоятельство существенно упрощает эксперимент и позволяет представить в графической форме и проанализировать полученные данные гораздо быстрее и с большей точностью.
Рассмотрим теперь простой способ нахождения комбинаций величин, входящих в формулу (4.2). используем так называемый релеевский метод решения размерных систем. Выразим сначала размерность переменных, описывающий систему с потерями на трение, по отношению к трем основным единицам: массы 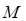 , времени
, времени 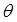 и длины
и длины 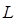 . Перечень формул размерностей для основных величин приводится в табл.4.1.
. Перечень формул размерностей для основных величин приводится в табл.4.1.
Допустим теперь, что между этими величинами существует следующее соотношение:
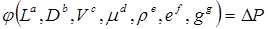 (4.3)
(4.3)
Подставим сюда вместо символов размерности из таблицы:
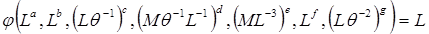 (4.4)
(4.4)
Таблица 4.1.Формулы размерностей
| Название переменной | Обозначение | Формула размерности |
| Потери тепла в трубе | 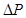 | 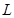 |
| Длина трубы | 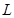 | 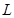 |
| Диаметр трубы | 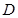 | 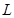 |
| Скорость потока жидкости | 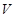 | 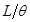 |
| Вязкость жидкости | 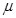 | 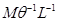 |
| Плотность жидкости | 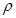 | 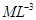 |
| Высота неровностей поверхности | 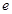 | 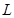 |
| Ускорение силы тяжести | 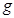 | 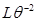 |
Чтобы данное уравнение было однородным относительно размерностей, должны выполняться следующие соотношения между показателями степени:
Для 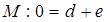 ,
,
Для 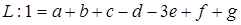 ,
,
Для 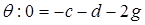
Имеем три уравнения с семью неизвестными. Упростим их, исключив 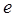 ,
, 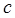 и
и 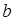 . Тогда
. Тогда 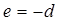 ,
, 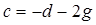 и
и 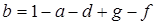 . Подставляя эти соот-ношения для показателей степени в формулу (4.3), поучаем:
. Подставляя эти соот-ношения для показателей степени в формулу (4.3), поучаем:
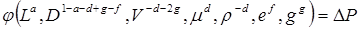 .
.
Объединяя члены с одинаковыми показателями степени, легко составить безразмерные комбинации:
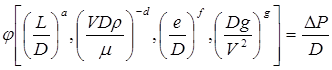 . (4.5)
. (4.5)
Восемь первоначальных переменных задачи дают пять безразмерных комбинаций. Применяя анализ размерностей, мы далеко продвинулись в реше-нии задачи. Теперь необходимо приступить к проверке фактической функции, в которую входят эти комбинации, и найти выражение, описывающее движение жидкости в трубе с потерями на трение. Эксперименты в области ламинарного потока дают следующую функцию:
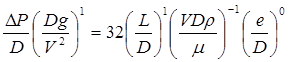 .
.
Далее будут рассмотрены некоторые способы, позволяющие получить это соотношение с помощью экспериментальных данных. Окончательным
результатом является известное уравнение для потерь на трение при ламинарном потоке в трубе круглого сечения
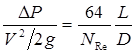 . (4.6)
. (4.6)
В данном случае имеется всего три безразмерные комбинации (четыре в случае турбулентного потока), хотя к этому выводу невозможно прийти лишь с помощью анализа размерностей. Однако совершенно очевидно, что анализ размерностей позволяет упростить эксперимент.
