Временные и спектральные представления сигналов

Министерство культуры Российской Федерации

Федеральное государственное бюджетное образовательное

учреждение высшего профессионального образования

«Санкт-Петербургский государственный университет

Кино и телевидения»

Кафедра технической электроники

А.В. Кривошейкин, Л.Х. Нурмухамедов

СХЕМОТЕХНИКА

АНАЛОГОВЫХ ЭЛЕКТРОННЫХ

УСТРОЙСТВ

Санкт-Петербург

УДК 621.375

Рецензенты

заведующий кафедрой звукотехники СПбГУКиТ

кандидат технических наук профессор К.Г. Ершов,

доцент кафедры радиотехники СПбСЗТУ

кандидат технических наук Л.В. Бессчётнова

Кривошейкин А.В., Нурмухамедов Л.Х. Схемотехника аналоговых электронных устройств: – СПб.: изд. СПбГУКиТ, 2012. – 199 с.

ISBN 978-5-94760-118-3

В монографии рассмотрены актуальные вопросы основы теории аналоговых электронных устройств, в частности энергетические показатели усилителя и вносимые усилителем искажения, применение обратной связи, методы синтеза и расчета принципиальных схем аналоговых трактов радиоэлектронной аппаратуры.

Издание предназначено для специалистов, работающих в области радиоэлектронной аппаратуры. Кроме того, оно будет полезно студентам, обучающимися по специальности 200700 «Радиотехника».

Рекомендовано к изданию Советом факультета аудиовизуальной техники СПбГУКиТ.

Протокол № 3 от 21 сентября 2011 г.

© Кривошейкин А.В., 2012

©Нурмухамедов Л.Х., 2012

ISBN 978-5-94760-118-3

Глава 1. ОБЩИЕ ПОЛОЖЕНИЯ

Аналоговые электронные устройства входят практически в состав любого современного радиотехнического оборудования.

Все аудио- и видеосигналы в окружающей нас среде являются аналоговыми сигналами (АС). Аналоговые электронные устройства (АЭУ) предназначены для обработки АС, в первую очередь для передачи, изменения параметров, хранения (запоминания). Основные типы АЭУ:

· усилители АС;

· фильтры;

· генераторы;

· устройства для изменения динамического диапазона - компандеры;

· аналого-цифровые (АЦП) и цифро-аналоговые (ЦАП) преобразователи;

· устройства автоподстройки частоты (АПЧ) и фазовой автоподстройки частоты (ФАПЧ);

· перемножители АС, коммутаторы, компараторы, и т.д.

Схемотехника изучает регулярные и нерегулярные методы проектирования АЭУ. Регулярные методы – синтез устройств на основе известных правил; нерегулярные методы – синтез устройств на основе итераций (идея – анализ – сопоставление результатов – переход к началу с изменением исходных данных). В процессе проектирования накапливается библиотека решений. Одна из задач данного курса – научиться «читать» и составлять схемы.

Сегодня в схемотехнике АЭУ широко применяется микроэлектроника: используются функционально законченные интегральные микросхемы (ИМС) с большой степенью интеграции.

В ряде случаев для обработки аналоговых сигналов используются цифровые методы.

Классы АЭУ

Все АЭУ можно разделить на 2 класса.

Линейные АЭУ. На выходе линейных АЭУ не возникают новые спектральные составляющие сигнала (но спектральный состав сигнала может изменяться). Примеры операций, выполняемых линейными АУ (линейных операций):

· усиление АС;

· фильтрация;

· коррекция частотных характеристик – амплитудно-частотной (АЧХ), фазочастотной (ФЧХ), группового времени и т. д.

Нелинейные АЭУ. На выходе нелинейных АЭУ возникают новые спектральные составляющие сигнала. Примеры нелинейных операций:

· перенос спектра АС, перемножение АС;

· амплитудное ограничение АС;

· изменение динамического диапазона;

· переключение АС и т. д.

Понятие о сигналах и их классификация

Сигналы представляют собой материальные носители информации. Материальным носителем информации (то есть сигналом) может быть вещество или силовое поле.

Сигналыклассифицируютпо разным основаниям.

По происхождению:

· естественные; обрабатывая их, мы познаём явления природы;

· искусственные.

По форме существования:

· статические (вещество) – книга, фонограмма, кинолента;

· динамические (поле) – электромагнитное (ЭМ) поле, акустическое поле.

По назначению (искусственные сигналы):

· связь и управление;

· измерение.

По физической природе:

· акустические;

· оптические;

· электрические;

· магнитные и др.

По структуре:

· непрерывные (аналоговые) – речь, музыка и т. д.;

· дискретные (цифровые) – например, телеграфные сигналы.

По месту в канале передачи:

· первичные – например, голос диктора;

· вторичные – радиоволна, фонограмма.

Передача информации сигналами возможна только тогда, когда получателю известны правила, по которым изменяется состояние канала передачи.

Временные и спектральные представления сигналов

1.3.1. Временные представления сигналов

Все сигналы являются функциями времени.

Сигналы связи, например звуковое сопровождение кинофильма, есть нестационарные случайные функции времени, или нестационарные случайные процессы. Сколько бы мы их ни наблюдали, мы не можем предсказать будущий сигнал. Будущее нестационарного случайного процесса неопределённо.

Измерительные сигналы описываются либо детерминированными, то есть определёнными, либо случайными функциями времени.

· Детерминированные функции времени: S = Asin ωt, периодическая последовательность импульсов, вообще – любая S = f(t), если f - известная нам функция;

· Для случайных функций времени невозможно заранее определить мгновенное значение S, поддаются определению только вероятностные характеристики.

1.3.2. Спектральные представления сигналов

Спектральные представления сигналов основаны на преобразовании Фурье.

Периодические функции, то есть определённые на интервале (– ∞, + ∞) и имеющие период Т, представляются рядом Фурье

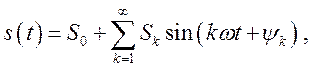(1.1)

где k = 1, 2, 3, . . . , ω = (2π/T);

S₀ – постоянная составляющая;

S_к – амплитудный спектр;

ψ_к – фазовый спектр.

Амплитудный и фазовый спектры периодического сигнала приведены на рис. 1.1.

Для непериодической функции связь между s (t) и её спектром определяется преобразованиями Фурье:

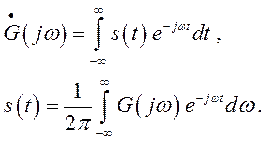(1.2)

Комплексная спектральная функция 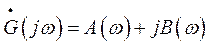позволяет определить амплитудный спектр сигнала через функцию спектральной плотности

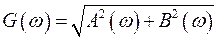(1.3)

и найти фазовый спектр 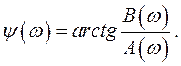(1.4)

Спектры непериодического сигнала приведены на рис. 1.2.

Мгновенный спектр учитывает изменчивость спектра во времени:

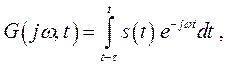(1.5)

то есть рассматривает спектр отрывка сигнала, занимающего интервал τ, предшествующий времени t.

Поскольку

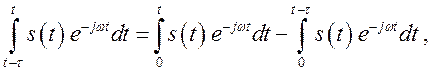
мгновенный спектр есть приращение текущего спектра за время τ.

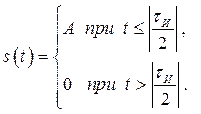Рис.1.3. Одиночный прямоугольный импульс

Например, чтобы найти спектр одиночного прямоугольного импульса (рис. 1.3), следует использовать выражение

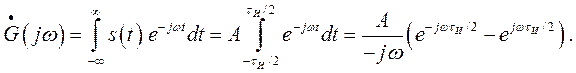
Поскольку 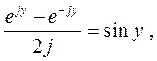то

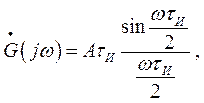
где Aτ_И – площадь импульса.

График модуля 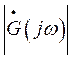приведён на рис. 1.4.

На частоте ω = 0 спектральная плотность 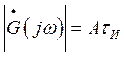равна площади импульса. Спектральная плотность обращается в нуль при

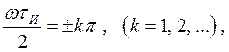или на частотах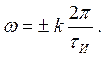

1.3.3. Практическое применение спектра сигнала

История спектрального анализа восходит к Бернулли, Эйлеру и Фурье (конец XVIII века). Фурье первый построил теорию разложения функций в тригонометрические ряды. Однако это разложение долгое время применялось как математический прием и не связывалось с какими-либо физическими понятиями. Спектральные представления применялись и развивались узким кругом физиков-теоретиков.

Начиная с 20-х годов XX века в связи с бурным развитием радиотехники и акустики спектральные разложения приобрели физический смысл и практическое применение. Основным средством анализа физических процессов стал гармонический анализ, а математической основой анализа стало преобразование Фурье. Преобразование Фурье разлагает произвольный сигнал на элементарные гармонические колебания с различными частотами, а все необходимые свойства и формулы выражаются с помощью двух действительных функций sin ωt, cos ωt. Гармонические колебания широко распространены в природе. Вся теория музыки базируется на использовании гармонических сигналов. В основе конструкции струнных музыкальных инструментов лежит струна, возбуждающая гармонические колебания, частота которых определяется длиной струны.

Поскольку гармонические колебания широко распространены в природе, то и смысл преобразования Фурье интуитивно понятен, независимо от математической аналитики. Таким образом, спектр сигнала – не математический фокус, а характеристика реально существующих физических процессов.

Свойства спектров:

· Периодические сигналы имеют линейчатый (дискретный) спектр. Спектральные составляющие периодического сигнала называются гармониками, они имеют кратные частоты.

· Непериодические сигналы имеют сплошной спектр.

· Если спектр ограничен, то есть занимает некоторую область от ω₁ до ω₂, то соответствующая ему функция времени бесконечна, то есть существует при - ∞ < t < ∞ .

· Если функция времени ограничена, то есть существует в интервале от t₁ до t₂ , то её спектр бесконечен.

· Спектр функции s(t) не зависит от выбора начала отсчёта времени.

· Спектр суммы двух или нескольких функций времени равен сумме их спектров.