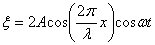Стоячие волны. Уравнение стоячей волны
Стоя́чая волна́ — явление интерференции волн, распространяющихся в противоположных направлениях, при котором перенос энергии ослаблен или отсутствует[1].
Стоячая волна (электромагнитная) — периодическое изменение амплитуды напряженности электрического и магнитного полей вдоль направления распространения, вызванное интерференцией падающей и отраженной волн[2].
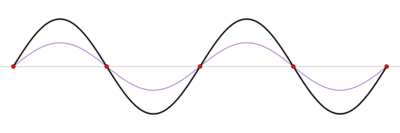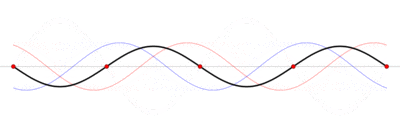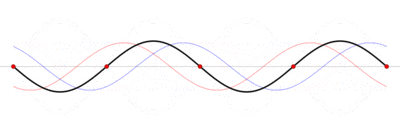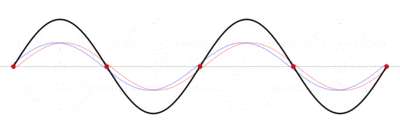
Стоячая волна — колебательный процесс в распределённых колебательных системах с характерным расположением чередующихся максимумов (пучностей) и минимумов (узлов) амплитуды. Такой колебательный процесс возникает, например, при отражении волны от преград и неоднородностей в результате взаимодействия (интерференции) падающей и отражённой волн. На результат интерференции влияют частота колебаний, модуль и фаза коэффициента отражения, изменение или сохранение поляризации волн при отражении и коэффициент затухания волн в среде распространения.
Строго говоря, стоячая волна может существовать только при отсутствии потерь в среде распространения (или в активной среде) и полном отражении падающей волны. В реальной среде существует режим смешанных волн: кроме стоячей волны присутствует и Бегущая волна, переносящая энергию к местам поглощения и излучения.
Примерами стоячей волны могут служить колебания струны, колебания воздуха в органной трубе[3]; в природе — волны Шумана. Для демонстрации стоячих волн в газе используют трубу Рубенса.
· 
Двумерная стоячая волна на диске. Основная мода
· 
Более высокая гармоника стоячей волны на диске
В случае гармонических колебаний в одномерной среде стоячая волна описывается формулой:
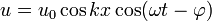 ,
,
где u — возмущения в точке х в момент времени t, 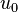 — амплитуда стоячей волны,
— амплитуда стоячей волны, 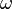 — частота , k — волновой вектор,
— частота , k — волновой вектор, 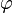 — фаза.
— фаза.
Стоячие волны являются решениями волновых уравнений. Их можно представить себе как суперпозицию волн, распространяющихся в противоположных направлениях.
При существовании в среде стоячей волны, существуют точки, амплитуда колебаний в которых равна нулю. Эти точки называются узлами стоячей волны. Точки, в которых колебания имеют максимальную амплитуду, называются пучностями.
Напишем уравнения двух плоских волн, распространяющихся вдоль оси х в противоположных направлениях:
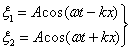
Сложив вместе эти уравнения и преобразовав результат по формуле для суммы косинусов, получим уравнение стоячей волны:
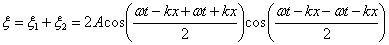
Преобразовав это уравнение, получим упрощенное уравнение стоячей волны: