Тема 10. Функции нескольких переменных

Функции двух и нескольких переменных. Частные производные и техника дифференцирования. Экстремум функции двух переменных и его необходимое условие. Понятие об эмпирических формулах и методе наименьших квадратов. Построение методом наименьших квадратов линейной функции по эмпирическим данным (вывод системы нормальных уравнений) ([1 или 6, § 15.1, 15.3, 15.6, 15.9]; [2 или 7, § 15.1 – 15.4], или [3, § 9.1, 9.3, 9.7, 9.10, 9.12 – 9.15], или [5, §5.1, 5.3, 5.7, 5.10, 5.12 – 5.15]).

Фактически мы ограничиваемся рассмотрением функции двух переменных. Для успешного усвоения этого раздела рекомендуется использовать метод аналогии с функциями одной переменной, хотя с увеличением числа переменных возникают существенные качественные отличия. Область определения функции двух переменных изображается множеством точек плоскости, а график – некоторой поверхностью в трехмерном пространстве ([1 или 6, пример 15.2] или [3, пример 9.2]).

В определении частной производной функции по одной из переменных используется понятие частного приращения, а в остальном оно сходно с определением производной функции одной переменной. Обратите внимание на способы обозначения частных производных. Техника дифференцирования функции двух (нескольких) переменных использует те же правила и приемы, которые применялись при нахождении производных функций одной переменной.

Для экстремума функции двух переменных формулируется определение и необходимое условие его существования ([1 или 6, § 15.6] или [3, § 9.7]), которые не являются достаточными.

Построение эмпирических формул методом наименьших квадратов имеет большое прикладное значение, в том числе в статистических и экономических исследованиях. Так как эмпирическая формула включает неизвестные параметры, то критерий, согласно которому она получается, является функцией этих параметров (функцией нескольких переменных). Параметры подбираются таким образом, чтобы критерий принял оптимальное (минимальное) значение. Возникает задача нахождения экстремума функции нескольких переменных – этим и объясняется рассмотрение в данном разделе метода наименьших квадратов.

Полученная методом наименьших квадратов эмпирическая формула является приближением таблично заданной функции.

Следует отметить, что погрешность построенного приближения f(x) оценивается величиной 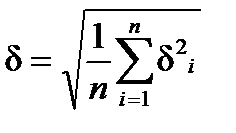, где 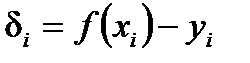, а n – число табличных значений (x_i, y_i). Используя полученное приближение, можно найти значения функций в точках, которые отличаются от табличных и лежат внутри отрезка (x₁, x_n) (интерполяция) или вне его (экстраполяция).

Раздел V. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ