Упражнения для аудиторной работы
Практикум по дифференциальной геометрии и топологии
Аудиторная работа № 11
Тема: Поверхности вращения. Линейчатые поверхности
Основные вопросы
1. Поверхности вращения
2. Линейчатые поверхности
Упражнения для аудиторной работы
1. Поверхность вращения. Пусть 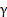 – гладкая кривая в плоскости Охz, заданная параметрическими уравнениями x = x(u)
– гладкая кривая в плоскости Охz, заданная параметрическими уравнениями x = x(u) 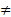 0, z = z(u), u
0, z = z(u), u 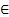 I, Г – поверхность, получаемая вращением кривой
I, Г – поверхность, получаемая вращением кривой 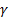 вокруг оси Оz.
вокруг оси Оz.
1) Запишите параметрические уравнения поверхности Г в декартовых координатах x, y, z, принимая в качестве параметров ее точки Р (х, у, z): параметр u точки Р′ пересечения кривой 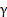 с плоскостью, проходящей через точку Р перпендикулярно оси Oz, и угол v между радиус-вектором проекции Р′′ точки Р на плоскость Оху и осью Ох.
с плоскостью, проходящей через точку Р перпендикулярно оси Oz, и угол v между радиус-вектором проекции Р′′ точки Р на плоскость Оху и осью Ох.
2) Является ли полученная параметризованная поверхность гладкой?
3) Что представляют собой координатные линии семейств u = const (параллели) и v = const (меридианы) поверхности вращения Г?
Ответ. 1) х = х(u) cos v, y = х(u) sin v, z = z(u), где (u;v) 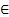 I х [0;
I х [0; 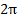 ).
).
2) Да.
3) Окружности и кривые, равные кривой 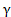 (нулевому меридиану).
(нулевому меридиану).
2. Поверхность получается вращением трактрисы x = sin u, y = 0, z = lntg  + cos u, u
+ cos u, u 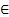 (0;
(0; 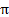 ), вокруг оси Оz (псевдосфера).
), вокруг оси Оz (псевдосфера).
1) Запишите ее параметрические уравнения в декартовых координатах x, y, z, выбирая параметры u и v, как в упражнении 1.
2) Что представляют собой координатные линии семейств u = const и v = const?
3) Сделайте эскиз поверхности; изобразите на нем по одной координатной кривой из каждого семейства.
Ответ. 1) х = sin u cosv, y = sin u sinv, z = lntg  + cos u, (u;v)
+ cos u, (u;v) 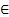 (0;
(0; 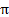 ) х [0;
) х [0; 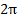 ).
).
2) Окружности (параллели) и кривые, равные трактрисе (меридианы).
3. Линейчатая поверхность. Пусть 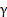 – гладкая кривая в пространстве, заданная векторным параметрическим уравнением
– гладкая кривая в пространстве, заданная векторным параметрическим уравнением 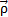 =
= 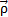 (u), u
(u), u 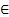 I, Г – поверхность, получаемая при движении прямой l (образующей) по кривой
I, Г – поверхность, получаемая при движении прямой l (образующей) по кривой 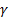 (направляющей), т.е. проходящей в процессе движения через каждую точку этой кривой.
(направляющей), т.е. проходящей в процессе движения через каждую точку этой кривой.
1) Запишите векторное параметрическое уравнение поверхности Г, принимая в качестве параметров ее точки Р: параметр u точки Р′ кривой 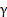 , через которую проходит образующая, содержащая точку Р, и «коэффициент коллинеарности» v векторов
, через которую проходит образующая, содержащая точку Р, и «коэффициент коллинеарности» v векторов 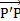 и
и 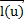 – орта этой образующей (
– орта этой образующей ( 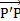 = v
= v 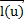 , v
, v 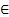 R).
R).
2) Что представляют собой координатные линии семейств u = const и v = const линейчатой поверхности Г?
Ответ.1) 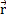 =
= 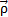 (u) + v
(u) + v 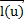 , u
, u 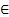 I, v
I, v 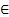 R.
R.
2) Координатная линия u = u0 – образующая, проходящая через точку направляющей 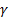 с параметром u0, координатная линия v = v0 – кривая на поверхности Г, расстояние от каждой точки которой до точки пересечения проходящей через нее образующей с кривой
с параметром u0, координатная линия v = v0 – кривая на поверхности Г, расстояние от каждой точки которой до точки пересечения проходящей через нее образующей с кривой 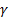 одно и то же и равно │v0│(эквидистанта).
одно и то же и равно │v0│(эквидистанта).
4.Запишите неявное уравнение цилиндрической поверхности в в декартовых координатах х, у, z, направляющей которой является окружность х2 + у2 = 1, z = 0, образующие которой параллельны вектору
 = (1; 1; 1).
= (1; 1; 1).
Ответ. (x – z)2 + (y – z)2 – 1 = 0.
Замечание. Цилиндрическая поверхность, очевидно, является линейчатой поверхностью, у которой все образующие параллельны. Поэтому ее векторное параметрическое уравнение можно записать в виде
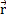 =
= 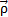 (u) + v
(u) + v 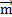 ,
,
где 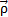 =
= 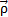 (u), u
(u), u 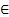 I, – уравнение любой ее направляющей,
I, – уравнение любой ее направляющей, 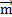 – постоянный вектор, параллельный ее образующим, v
– постоянный вектор, параллельный ее образующим, v 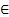 R.
R.
5.Запишите неявное уравнение конической поверхности в декартовых координатах х, у, z, вершиной которого является точка В (1; 1; 1), а образующими – прямые, проходящие через точки окружности х2 + у2 = 1, z = 0.
Ответ. (x – z)2 + (y – z)2 – (z – 1)2 = 0.
Замечание. Коническая поверхность, очевидно, является линейчатой поверхностью, у которой направляющей является точка (вершина конуса). Поэтому ее векторное параметрическое уравнение можно записать в виде
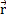 =
= 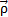 + v
+ v 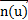 ,
,
где 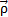 – радиус-вектор вершины конуса (постоянный вектор),
– радиус-вектор вершины конуса (постоянный вектор), 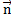 =
= 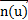 , u
, u 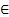 I, – вектор с началом в вершине конуса и концом в точке любой его направляющей (отличной от вершины) с параметром u, v
I, – вектор с началом в вершине конуса и концом в точке любой его направляющей (отличной от вершины) с параметром u, v 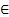 R.
R.
