Практические задачи управления запасами

Задача 1. Управление запасами

1. На нефтебазу бензин привозят на танкере. Накладные расходы g в расчете на партию бензина составляют 50000 руб. Ежегодно база отпускает µ = 4000 т бензина. Затраты на хранение h примем равным 0,5 руб. за 1 т бензина в сутки. Поставка осуществляется по первому требованию – мгновенно, и дефицит бензина на базе не допускается. Найдите оптимальные: объем заказываемой партии q, длительность цикла Т^* работы системы и общие среднесуточные издержки .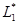

Решение:

Для решения задачи используем формулы Уилсона, наиболее часто применяемые при подобных расчетах.

1. Оптимальный размер заказываемой партии рассчитаем по формуле:

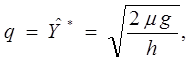3.1

где: q – объем заказываемой партии;

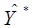- предельный запас на складе (вследствие того, что поставка осуществляется по первому требованию и дефицит бензина на базе не допускается );

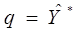g - накладные расходы;

µ - интенсивность спроса;

h - затраты на хранение.

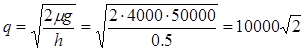т.

2. Интервал между заказами рассчитаем по формуле:

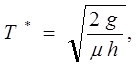3.2

где: Т^* - длительность цикла работы системы;

g - накладные расходы;

µ - интенсивность спроса;

h - затраты на хранение.

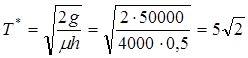сут.

3. Общие среднесуточные издержки рассчитаем по формуле:

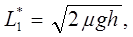3.3

где: 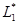- общие среднесуточные издержки;

g - накладные расходы;

µ - интенсивность спроса;

h - затраты на хранение.

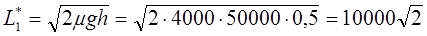руб./сут.

Задача 2. Управление запасами

Завод радиоэлектронной аппаратуры производит 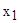радиоприемников в сутки. Микросхемы для радиоприемников (по 1 шт. на приемник) производятся на этом же заводе с интенсивностью 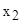тыс. шт. в сутки. Затраты на подготовку производства партии микросхем составляют 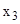руб. (числа в задаче условные), себестоимость производства 1 тыс. шт. микросхем равна 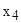руб. Хранение микросхем на складе обходится заводу в 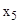руб. за каждую тысячу в сутки. У завода появилась возможность закупать микросхемы в другом месте по цене 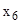руб. за 1 тыс. шт. Стоимость доставки равна 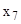руб.

Выясните, стоит ли заводу закупать микросхемы вместо того, чтобы их производить. Для более выгодного режима работы завода (производство или закупка) определите периодичность подачи заказа, и затраты на управление запасами в месяц (22 рабочих дня).

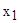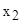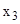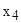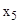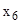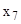			4,2	2,5

Решение:

Так как сумма стоимости покупных микросхем и затрат на их доставку (S1 = x6 + x7 =4+78 = 82) меньше суммы себестоимости производимых и затрат на подготовку производства партии (S2 = x3 + x4 = 92+4,2 = 96,2), то заводу выгоднее закупать микросхемы.

Периодичность подачи заказов определяется по формуле:

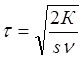
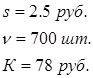
Периодичность подачи заказа:

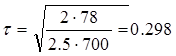
Затраты на управление запасами в месяц:

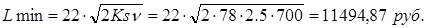
Заключение

Запасы различного рода играют важнейшую роль при функционировании любой экономической системы и возникают практически во всех звеньях народного хозяйства.

Ни одно производственное предприятие не может существовать без материально-производственных запасов. От их объема и уровня в значительной мере зависят результаты коммерческой деятельности предприятия. Они чутко реагируют на любые изменения рыночной конъюнктуры, и, в первую очередь, на отношение спроса и предложения. Сам факт их существования не приносит их владельцам ничего, кроме затрат и убытков.

В качестве материально-производственных запасов принимаются активы: используемые при производстве продукции (выполнение работ, оказание услуг), предназначенной для продажи (сырье и основные материалы, покупные полуфабрикаты); предназначенные для продажи (готовая продукция и товары); используемые для управленческих нужд организации (вспомогательные материалы, топливо, запасные части).

Основная часть материально-производственных запасов используется в качестве предметов труда в производственном процессе. Они целиком потребляются в каждом производственном цикле и полностью переносят свою стоимость на стоимость производимой продукции.

Управление запасами направленно на повышение рентабельности и скорости обращения вложенного капитала.

Задача управления запасами возникает, когда необходимо создать запас материальных ресурсов или предметов потребления с целью удовлетворения спроса на заданном интервале времени (конечном или бесконечном). Для обеспечения непрерывного и эффективного функционирования практически любой организации необходимо создание запасов. В любой задаче управления запасами требуется определять количество заказываемой продукции и сроки размещения заказа. Спрос можно удовлетворить путём однократного создания запаса на весь рассматриваемый период времени или посредством создания запаса для каждой единицы времени этого периода. Эти два случая соответствуют избыточному запасу (по отношению к единице времени) и недостаточному запасу (по отношению к полному периоду времени).

При избыточном запасе требуется более высокие удельные (отнесённые к единице времени) капитальные вложения, но дефицит возникает реже и частота размещения заказов меньше. С другой стороны, при недостаточном запасе удельные капитальные вложения снижаются, но частота размещения заказов и риск дефицита возрастает. Для любого из указанных крайних случаев характерны значительные экономические потери. Таким образом, решения относительно размера заказа и момента его размещения могут основываться на минимизации соответствующей функции общих затрат, включающих затраты, обусловленные потерями от избыточного запаса и дефицита.

С помощью математических методов можно выработать правила управления запасами. Что и было сделано в курсовой работе.

Список использованной литературы:

1. Акулич И.Л. Математическое программирование в примерах и задачах. — М.: Высшая школа, 1986.

2. Аронович А.Б., Афанасьев М.Ю., Суворов Б.П. Сборник задач по исследованию операций. — М.: Издательство Московского университета, 1997.

3. Кивачук В.С. Оздоровление предприятия: экономический анализ. Издательства: Издательство деловой и учебной литературы, «Амалфея». М.: 2002 г.

4. Монахов А.В. Математические методы анализа экономики. СПб.: Издательство «Питер», серия «Краткий курс», 2002 г.

5. Морозов В.В., Сухарев А.Г., Федоров В.В. Исследование операций в задачах и упражнениях. - М.: Высшая школа, 1986.

6. Пинегина М.В. Математические методы и модели в экономике. М.: Издательство «Экзамен», 2002 г.

7. Пястолов С.М. Экономический анализ деятельности предприятий: Учебное пособие для вузов Серия: «Gaudeamus». М.: 2002 г.

8. Фомин Г.П. математические методы и модели в коммерческой деятельности: Учебник. - М.: Финансы и статистика, 2001.

9. Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении. М.: Издательство «Дело», серия «Наука управления», 2000г

10. Шикин Е.В., Чхартишвили А.Г. Математические методы и модели управления. - М.: Дело, 2000.