Ограниченность функции

Будем называть функцию y=f(x) ОГРАНИЧЕННОЙ СВЕРХУ (СНИЗУ) на множестве А из области определения D(f), если существует такое число M, что для любых x из этого множества выполняется условие

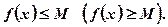
При помощи логических символов определение может быть записано в виде:

f (x) – ограничена сверху на множестве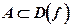

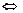
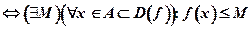(8. 15)

( f (x) – ограничена снизу на множестве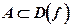

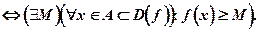(8. 16)

Вводятся в рассмотрение и функции, ограниченные по модулю или просто ограниченные.

Будем называть функцию 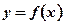ОГРАНИЧЕННОЙ на множестве А из области определения 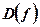, если существует положительное число M, что

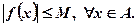
На языке логических символов

f(x) – ограничена на множестве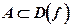

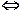
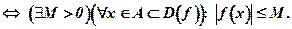(8. 17)

Функция, не являющаяся ограниченной, называется неограниченной. Мы знаем, что определения, данные через отрицание, малосодержательны. Чтобы сформулировать это утверждение как определение, воспользуемся свойствами кванторных операций (3.6) и (3.7). Тогда отрицание ограниченности функции на языке логических символов даст:

________

f(x) – ограничена на множестве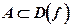

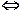
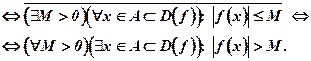
Полученный результат позволяет сформулировать следующее определение.

Функция 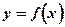называется НЕОГРАНИЧЕННОЙ на множестве А, принадлежащем области определения функции, если на этом множестве для любого положительного числа М найдется такое значение аргумента х, что значение 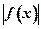все равно превзойдет величину М, то есть .

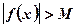В качестве примера рассмотрим функцию

.

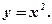Она определена на всей действительной оси. Если взять отрезок [–2;1] (множество А), то на нем она будет ограничена и сверху, и снизу.

Действительно, чтобы показать ее ограниченность сверху, надо рассмотреть предикат

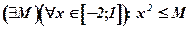
и показать, что найдется (существует) такое М, что для всех x, взятых на отрезке [–2;1], будет справедливо

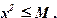
Найти такое М не представляет труда. Можно считать М = 7, квантор существования предполагает отыскание хотя бы одного значения М. Наличие такого М и подтверждает тот факт, что функция на отрезке [–2;1] ограничена сверху.

Чтобы доказать ее ограниченность снизу, надо рассмотреть предикат

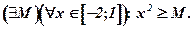
Значением М, обеспечивающим истинность данного предиката, является, например, М = –100.

Можно доказать, что функция 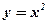будет ограничена и по модулю: для всех x из отрезка [–2;1] значения функции 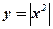совпадают со значениями 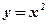, поэтому в качестве М можно взять, к примеру, прежнее значение М = 7.

Покажем, что та же функция, но на промежутке 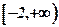, будет неограниченной, то есть

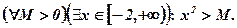
Чтобы показать, что такие x существуют, рассмотрим утверждение

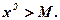
Отыскивая искомые значения x среди положительных значений аргумента, получим

.

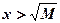Это значит, что какое бы положительное Ммы ни брали, значения x, обеспечивающие выполнение неравенства

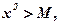
получаются из соотношения .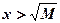

Рассматривая функцию 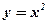на всей действительной оси, можно показать, что она неограничена по модулю.

Действительно, из неравенства

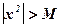
следует

.

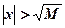То есть, каким бы большим ни было положительное M, 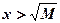или 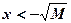обеспечат выполнение неравенства .

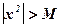ЭКСТРЕМУМ ФУНКЦИИ.

Приведите примеры функций, описывающих объекты реального мира, у которых: а) локальный минимум превосходил бы локальный максимум; б) локальный минимум был бы положительным, а локальный максимум отрицательным.

Функция 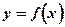имеет в точке с локальный максимум (минимум), если существует такая окрестность этой точки, что для x¹с из этой окрестности выполняется неравенство

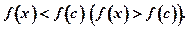
Сформулируйте определения локального максимума и локального минимума на языке математической логики.

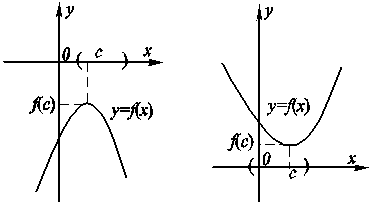а) б)   Рис. 8.7. Экстремумы функции.

Точки локального мак-симума (рис. 8.7, а) и локального минимума (рис. 8.7, б) называют точками ЛОКАЛЬНОГО ЭКСТРЕ-МУМА. Иногда слово “локаль-ный” опускают и просто говорят о максимумах, минимумах, экстремумах функции. Вместе с тем, экстремум – свойство локальное, характеризующее поведение функции в точке путем сравнения ее значений со значениями в точках области определения, близлежащих к данной. Отметим

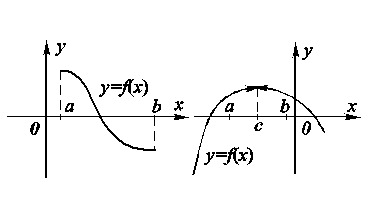а) б)   Рис. 8.8. Случаи отсутствия экстремума.

особо, что точка экстремума может быть только внутренней точкой промежутка и f(x) в ней должна быть обязательно определена. Возможные случаи отсутствия экстремума изображены на рис. 8.8.

Если функция возрастает (убывает) на некотором промежутке 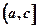иубывает (возрастает) на некотором промежутке 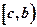, то точка с является точкой локального максимума (минимума).

Отсутствие максимума функции f(x) в точке с можно сформулировать так:

_______________________

f(x) имеет максимум в точке c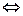

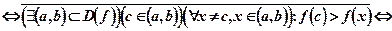
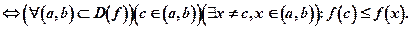
Это означает, что если точка c не есть точка локального максимума, то какой бы ни была окрестность, включающая в себя точку cкак внутреннюю, в ней найдется хотя бы одно значение x не равное c, при котором 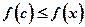. Таким образом, если в точке c нет максимума, то в этой точке экстремума может не быть вообще или же это точка минимума (рис. 8.9).

а) б)     Рис. 8.9. Возможные случаи отсутствия максимума в точке .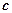

Понятие экстремума дает сравнительную оценку значения функции в какой-либо точке по отношению к близлежащим. Подобное сравнение значений функций можно провести и для всех точек некоторого промежутка.

НАИБОЛЬШИМ (НАИМЕНЬШИМ) значением функции 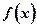на множестве 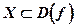будем называть ее значение в точке 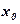из этого множества такое, что

.

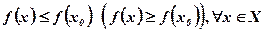Наибольшее (наименьшее) значение функции называют еще глобальным максимумом (минимумом) функции. Точки глобального максимума и минимума называют точками глобального экстремума. Их количество может быть конечным или же бесконечным, или же этих точек может не существовать вообще.

Например, функция

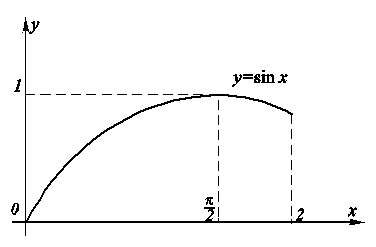Рис. 8.10. Наибольшее и наименьшее значения функции на отрезке .

на отрезке 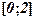(рис. 8.10) принимает наибольшее значение, равное 1, в точке 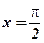, а наименьшее значение, равное 0, – при 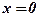. Наибольшее значение функции достигается во внутренней точке отрезка 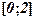, а наименьшее – на его левом конце.

Чтобы определить наибольшее (наименьшее) значение функции, заданной на отрезке, надо среди всех значений ее максимумов (минимумов), а также значений, принимаемых на концах промежутка, выбрать наибольшее (наименьшее) число. Оно и будет наибольшим (наименьшим) значением функции. Это правило будет уточнено в дальнейшем.

Проблема отыскания наибольшего и наименьшего значений функции на открытом промежутке не всегда решается достаточно легко. Например, функция

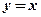
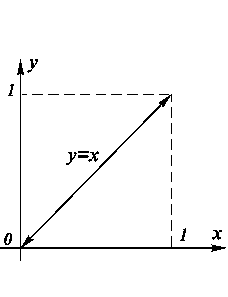Рис. 8.11. Пример функции, не имеющей наибольшего и наименьшего значений в интервале (0;1).

в интервале 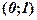(рис. 8.11) их не имеет.

Убедимся, например, что эта функция не имеет наибольшего значения. В самом деле, учитывая монотонность функции 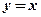, можно утверждать, что как бы близко мы ни задавали слева от единицы значения х, найдутся другие х, в которых значения функции будут больше ее значений во взятых фиксированных точках, но все же меньше единицы.