Функция. Монотонность. Ограниченность

Лекция №1

Тема: Введение

Условные обозначения:

: - так, что def – по определению

Ì – включает ’’’ – [dⁿf(x)]/dxⁿ=(d/dx)([d^n-1f(x)]/dxⁿ)

Þ - следует, выполняется

Û - тогда и только тогда

" - любой

$ - существует

] – пусть

! – единственный

[x] – целая часть

~ - эквивалентно

о - малое

Все Rпредставляют десятичной дробью.

Все Q представляют конечной дробью, либо периодичной дробью.

Все иррациональные числа представляют бесконечной десятичной дробью ( не периодичной).

Рассмотрим числовую ось. Числовая ось – направленная прямая с отмеченной точкой и отмеченным масштабом.

	x

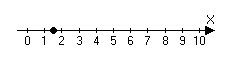
0 – отвечает за ноль.

Отрезок [0;1] отвечает за единицу

Единица за единицу.

Каждой точки х на числовой прямой отвечает некоторое действительное число. Если длинны отрезков [0;x] из заданного масштаба соизмеримы, тогда числу х отвечает рациональное число. Если не соизмеримы, то иррациональны.

Каждому Rотвечает точка на числовой прямой и наоборот, каждой точке отвечает R.

Основные числовые множества.

x

Отрезок: [/////////] x

a b

Обозначается [a;b] a£b

Частный случай отрезка точка

Или a£x£b – в виде неравенства.

х

Интервал: (/////////) x – множество точек на числовой прямой.

a b

Обозначается (a;b) или в виде неравенства a<x<b

x

Полуинтервал: (/////////] x

a b

x

[/////////) x

a b

Обозначается: [a;b) a£x£b

(a;b] a<x£b

Всё это числовые промежутки.

Замечание: один из концов ( а или b) может быть символом ±¥.

x

///////////////] x (-¥;b] или -¥<x£b

b

x

///////////////) x (-¥;b) или -¥<x<b

b

Вся числовая прямая – R=(-¥;+¥)

Окрестности.

Определение: ε –окрестностью числа а называется множество чисел х удовлетворяющие неравенству

a-ε<x<a+ε Û |x-a| Û (////·////) x Û О_ε(а)

ε>0 а-ε а а+ε

О_ε(а)={xÎR:|x-a|<ε}

Проколотая ε окрестность – О^°_ε(а) это множество таких чисел включающих R, и отстаёт от точки на ε и не принадлежит а.

О^°_ε(а)={xÎR:0<|x-a|<ε}

(////°////) x

а-ε а а+ε

Правая ε поло окрестность точки а: О⁺_ε(а)={xÎR:a£x<a+ε}

· ///////) x

a a+ε

Проколотая правая ε поло окрестность точки а: О^°_ε(а)={xÎR:a<x<a+ε} Рисунок подобен предыдущему только с выколотой точкой а.

Левая ε поло окрестность точки а: O^-_ε(a)={xÎR:a-ε<x£a}

(////////· x

a-ε a

Проколотая, левая ε поло окрестность точки а: О^°-_ε(а)={xÎR:a-ε<x<a} Рисунок подобен предыдущему только с выколотой точкой а.

Модуль и основные неравенства.

x; x>0

|х|= 0; x=0

-x; x<0

|x|<h Û -h<x<h |x|>hÛ x>h

h>0 x<-h

1) " а,b Î R: |a±b|£|a|+|b|

2) " а,b Î R: |a-b|³||a|-|b||

Можно рассматривать окрестности бесконечности:

О_ε(+¥)={xÎR:x>ε} (////////// x

ε>0 ε

О_ε(-¥)={xÎR:x<-ε} ///////////) · x

ε>0 -ε 0

О_ε(¥)={xÎR:|x|>ε} \\\\\\) _· (////// x

x>ε;x<-ε -ε ε

Функция. Монотонность. Ограниченность.

х – называется независимой переменной.

у – зависимой.

Функцию можно задавать равенством (у=х²)

Таблицей

Х	Х1	Х2	Х3	Х4
У	У1	У2	У3	У4

Графиком, то есть множеством точек с координатами (x,f(x)) на плоскости:

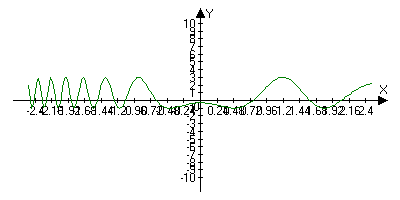
Определение f(x) монотонности: Пусть Х принадлежит области определение D ( ]xÌD)

Пусть Х подмножество в области определения в f(x).

Функция у=f(x) называется:

1) Возрастающая на Х, если для любого х₁;х₂ принадлежащие Х: х₁<x₂Þf(x₁)<f(x₂)

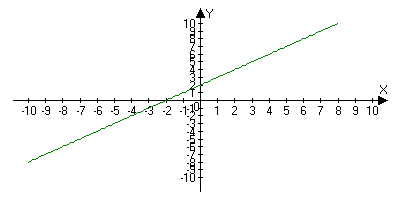
2) Убывающий на Х, если для любого х₁;х₂ принадлежащие Х: х₁<x₂Þf(x₁)>f(x₂)

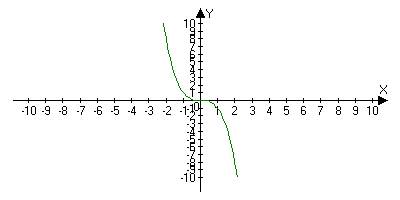
3) Не убывающий на Х, если для любого х₁;х₂ принадлежащие Х: х₁<x₂Þf(x₁)£f(x₂)

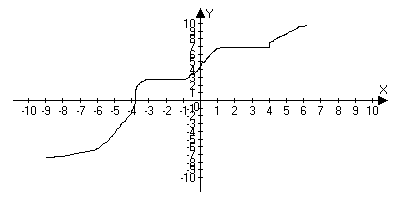
4 Не возрастающая на Х, если для любого х₁;х₂ принадлежащие Х: х₁<x₂Þf(x₁)³f(x₂)

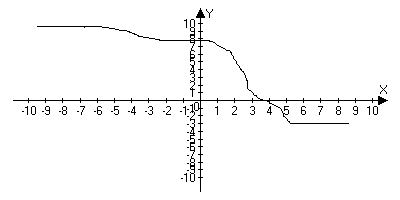
Определение:

Ограниченность. Пусть Х включает D y=f(x) называется:

1) Ограниченной сверху на Х если существует В, так что для любого х принадлежащего Х выполняется x£R

2) Ограниченной снизу на Х если существует А, так что для любого х принадлежащего Х выполняется А£х

3) Ограниченной и сверху и снизу на Х если существует А,В, так что для любого х принадлежащего Х выполняется А£х£В, или существует С, так что для любого х принадлежащего Х выполняется |х|£С