Частные производные. Примеры решений

На данном уроке мы познакомимся с понятием функции двух переменных, а также подробно рассмотрим наиболее распространенное задание – нахождение частных производныхпервого и второго порядка, полного дифференциала функции.

Для эффективного изучения нижеизложенного материала Вам необходимо уметь более или менее уверенно находить «обычные» производные функции одной переменной. Научиться правильно обращаться с производными можно на уроках Как найти производную? и Производная сложной функции. Также нам потребуется таблица производных элементарных функций и правил дифференцирования, удобнее всего, если она будет под рукой в распечатанном виде.

Начнем с самого понятия функции двух переменных, постараемся ограничиться минимумом теории, так как сайт имеет практическую направленность. Функция двух переменных обычно записывается как 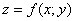, при этом переменные 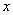, 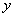называются независимыми переменными или аргументами.

Пример: 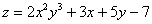- функция двух переменных.

Иногда используют запись 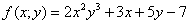. Также встречаются задания, где вместо буквы 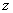используется буква .

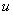Полезно знать геометрический смысл функций. Функции одной переменной 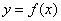соответствует определенная линия на плоскости, например, 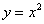– всем знакомая школьная парабола. Любая функция двух переменных 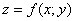с геометрической точки зрения представляет собой поверхность в трехмерном пространстве (плоскости, цилиндры, шары, параболоиды и т.д.). Но, собственно, это уже аналитическая геометрия, а у нас на повестке дня математический анализ.

Переходим к вопросу нахождения частных производных первого и второго порядков. Должен сообщить хорошую новость для тех, кто выпил несколько чашек кофе и настроился на невообразимо трудный материал: частные производные – это почти то же самое, что и «обычные» производные функции одной переменной.

Для частных производных справедливы все правила дифференцирования и таблица производных элементарных функций.Есть только пара небольших отличий, с которыми мы познакомимся прямо сейчас.

Пример 1

Найти частные производные первого и второго порядка функции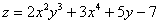

Сначала найдем частные производные первого порядка. Их две.

Обозначения:

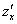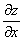или – частная производная по «икс»

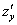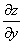или – частная производная по «игрек»

Начнем с .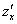

Важно! Когда мы находим частную производную по «икс», то переменная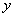 считается константой (постоянным числом).

Решаем. На данном уроке будем сразу приводить полное решение, а комментарии давать ниже.

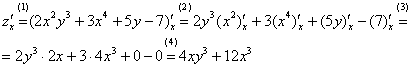
Комментарии к выполненным действиям:

(1) Первое, что мы делаем при нахождении частной производной – заключаем всюфункцию в скобки под штрих с подстрочным индексом.

Внимание, важно!Подстрочные индексы НЕ ТЕРЯЕМ по ходу решения. В данном случае, если Вы где-нибудь нарисуете «штрих» без 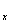, то преподаватель, как минимум, может поставить рядом с заданием 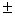(сразу откусить часть балла за невнимательность).

Далее данный шаг комментироваться не будет, все сделанные замечания справедливы для любого примера по рассматриваемой теме.

(2) Используем правила дифференцирования 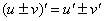; 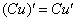. Для простого примера, как этот, оба правила вполне можно применить на одном шаге. Обратите внимание на первое слагаемое: так как 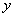считается константой, а любую константу можно вынести за знак производной, то 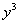мы выносим за скобки. То есть в данной ситуации 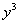ничем не лучше обычного числа. Теперь посмотрим на третье слагаемое 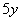: здесь, наоборот, выносить нечего. Так как 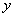константа, то 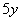– тоже константа, и в этом смысле она ничем не лучше последнего слагаемого – «семерки».

(3) Используем табличные производные 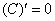и .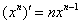

(4) Упрощаем ответ.

Теперь определим 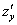. Когда мы находим частную производную по «игрек», то переменная 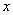считается константой (постоянным числом).

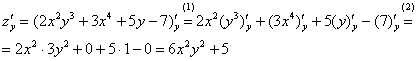
(1) Используем те же правила дифференцирования 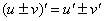; 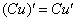. В первом слагаемом выносим константу 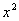за знак производной, во втором слагаемом ничего вынести нельзя поскольку 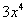– уже константа.

(2) Используем таблицу производных элементарных функций. Мысленно поменяем в таблице все «иксы» на «игреки». То есть данная таблица рАвно справедлива для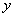 (и вообще для любой буквы).В данном случае, используемые нами формулы имеют вид: 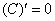и .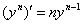

Итак, частные производные первого порядка найдены