Сформулируйте и поясните необходимое и достаточное условия монотонности функции и существования экстремума функции в точке.

Вопросы к экзамену

Определите понятия комплексного числа и арифметических операций над ними. Дайте представление о формах представления комплексных чисел.

Объясните графическое изображение комплексного числа и множества комплексных чисел.

Определите понятие комплексного числа. Поясните методы решения уравнений над множеством комплексных чисел.

Определите и поясните на примерах понятие матрицы и арифметических операций над матрицами.

Сформулируйте понятие определителя и свойства определителей.

Дайте определение минора и алгебраического дополнения элемента определителя. Сформулируйте правила разложения определителя по строке или столбцу.

Определите понятие обратной матрицы, формулу для ее вычисления. Объясните решение матричных уравнений.

Определите понятия системы линейных уравнений, совместных и эквивалентных систем. Поясните решение систем линейных уравнений с помощью формул Крамера.

Определите понятия системы линейных уравнений, совместных и эквивалентных систем. Поясните решение систем линейных уравнений с помощью метода Гаусса.

Воспроизведите виды уравнений прямых на плоскости, сформулируйте признаки параллельности и перпендикулярности прямых, формулу расстояния от точки до прямой.

Определите понятие вектора в пространстве, линейных операций над векторами. Определите декартову систему координат в пространстве.

Определите понятие скалярного произведения векторов и его свойства.

Определите понятие векторного произведения векторов и его свойства.

Определите понятие смешанного произведения векторов и его свойства.

Воспроизведите и объясните уравнение плоскости в пространстве.

Воспроизведите и объясните уравнение прямой в пространстве.

Воспроизведите уравнения эллипса и параболы, изобразите их на чертеже.

Воспроизведите уравнение гиперболы, изобразите ее на чертеже.

Сформулируйте понятие предела функции в точке и на бесконечности. Определите понятия бесконечно малых и бесконечно больших функций, их свойства.

20. Объясните правила раскрытия неопределенностей 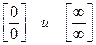при вычислении пределов функций.

Сформулируйте замечательные пределы. Объясните правила раскрытия неопределенностей при вычислении пределов функций.

Определите и поясните понятие непрерывности функции в точке. Дайте классификацию точек разрыва. Сформулируйте свойства непрерывных функций.

Определите понятие производной функции в точке, поясните ее геометрический и механический смысл. Составьте уравнение касательной.

Сформулируйте и поясните на примерах основные правила дифференцирования.

Сформулируйте и поясните правила дифференцирования сложной функции.

Сформулируйте правило Лопиталя и поясните его применение.

Сформулируйте понятие дифференциала 1-го порядка и производных высших порядков.

Сформулируйте и поясните необходимое и достаточное условия монотонности функции и существования экстремума функции в точке.