Возведение комплексных чисел в натуральную степень
ИКТИБ ИТА ЮФУ
КУРС ЛЕКЦИЙ ПО МАТЕМАТИКЕ
Лекция 2 Комплексные числа (часть 2)
Что главное мы узнали на прошлой лекции
Мы познакомились с алгебраической (декартовой) формой 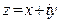 записи комплексных чисел, геометрическим смыслом линейных операций над комплексными числами: сложением , вычитанием и умножения на действительное число. Это, по сути, свойства линейных операций с векторами на плоскости.
записи комплексных чисел, геометрическим смыслом линейных операций над комплексными числами: сложением , вычитанием и умножения на действительное число. Это, по сути, свойства линейных операций с векторами на плоскости.
Если заменить декартову систему координат на плоскости на так называемую полярную систему координат, то удается установить геометрический смысл нелинейных операций над комплексными – умножением и делением комплексных чисел.
При переходе к полярной системе координат декартовы координаты 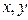 заменяются на полярные координаты
заменяются на полярные координаты 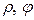 , которые также однозначно определяют положение точки на плоскости. Формулы
, которые также однозначно определяют положение точки на плоскости. Формулы 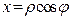 ,
, 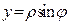 являются формулами перехода к полярной системе координат плоскости.
являются формулами перехода к полярной системе координат плоскости.
Что мы узнаем на этой лекции
Мы продолжим изучение геометрического смысла нелинейных операций над комплексными. Теперь это будут операции возведения в натуральную степень и извлечения корня из комплексных чисел.
Также мы узнаем о некоторых важных свойствах многочленов и решении алгебраических уравнений.
Возведение комплексных чисел в натуральную степень
Пусть задано комплексное число 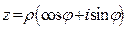 в тригонометрической форме. Какое получится число при возведении его в квадрат? Так как при комплексных чисел модули этих чисел перемножаются, а аргументы складываются, то при возведении в квадрат модуль комплексного числа возводится в квадрат, а аргумент умножается на 2.
в тригонометрической форме. Какое получится число при возведении его в квадрат? Так как при комплексных чисел модули этих чисел перемножаются, а аргументы складываются, то при возведении в квадрат модуль комплексного числа возводится в квадрат, а аргумент умножается на 2.
При возведении комплексного числа в 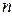 -ю степень модуль этого комплексного числа возводится в
-ю степень модуль этого комплексного числа возводится в 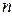 -ю степень, а аргумент умножается на
-ю степень, а аргумент умножается на 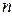 . Итак, справедлива формула
. Итак, справедлива формула 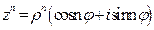 . Это выражение называется формулой Муавра.
. Это выражение называется формулой Муавра.
8. Извлечение корня 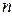 -й степени из комплексных чисел
-й степени из комплексных чисел
Пусть задано комплексное число 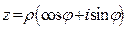 в тригонометрической форме. Какое число при возведении его в
в тригонометрической форме. Какое число при возведении его в 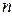 -ю степень даст нам число, модуль которого равен
-ю степень даст нам число, модуль которого равен 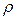 , а аргумент равен
, а аргумент равен 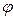 ? Так как возведении комплексного числа в
? Так как возведении комплексного числа в 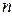 -ю степень модуль этого комплексного числа возводится в
-ю степень модуль этого комплексного числа возводится в 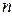 -ю степень, а аргумент умножается на
-ю степень, а аргумент умножается на 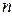 , то, очевидно, комплексное число с модулем, равным
, то, очевидно, комплексное число с модулем, равным 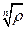 и аргументом, равным
и аргументом, равным 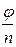 , обладает требуемым свойством. Обратим внимание на то, что при изменении аргумента на значение, равное
, обладает требуемым свойством. Обратим внимание на то, что при изменении аргумента на значение, равное 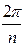 , после возведения в
, после возведения в 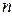 -ю степень комплексное число изменяет значение аргумента на
-ю степень комплексное число изменяет значение аргумента на 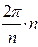 , т.е. на
, т.е. на 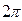 . А это означает, что таким образом измененное комплексное число также является корнем
. А это означает, что таким образом измененное комплексное число также является корнем 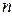 -й степени из заданного числа
-й степени из заданного числа 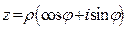 .
.
Тем самым мы приходим к формуле 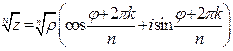 , где
, где 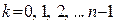 .
.
Итак, 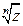 является величиной, принимающей
является величиной, принимающей 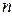 различных значений при
различных значений при 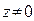 . Заметим, что все эти значения корня лежат на окружности радиуса
. Заметим, что все эти значения корня лежат на окружности радиуса 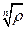 через равные значения аргумента
через равные значения аргумента 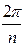 .
.
Пример 2. Найдите модуль и аргумент комплексного числа 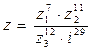 , где
, где 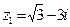 ,
, 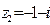 ,
, 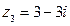 .
.
Решение. План действий следующий. Мы найдем модуль и аргумент чисел 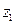 ,
, 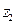
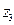 . Затем мы найдем искомый модуль числа, учитывая, что при возведении в степень модуль возводится в эту же степень, при перемножении комплексных чисел их модули перемножаются, при делении – соответствующие модули делятся. После этого мы займемся аргументами чисел
. Затем мы найдем искомый модуль числа, учитывая, что при возведении в степень модуль возводится в эту же степень, при перемножении комплексных чисел их модули перемножаются, при делении – соответствующие модули делятся. После этого мы займемся аргументами чисел 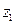 ,
, 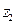
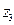 и, учитывая соответствующие правила для аргументов, найдем искомый аргумент.
и, учитывая соответствующие правила для аргументов, найдем искомый аргумент.
Рассмотрим число 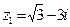 и вычислим его модуль и вычислим его модуль 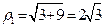 . Найдем тангенс аргумента этого числа . Найдем тангенс аргумента этого числа 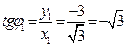 . Так как . Так как 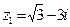 находится в 4-й четверти, то главное значение его аргумента находится в 4-й четверти, то главное значение его аргумента 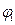 равно равно 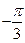 . . | 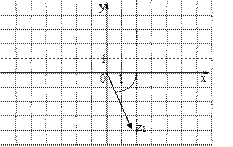 |
Рассмотрим теперь число 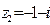 и вычислим его модуль и вычислим его модуль 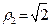 . Найдем тангенс аргумента этого числа . Найдем тангенс аргумента этого числа 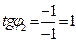 . Так как точка . Так как точка 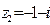 находится в 3-й четверти, то главное значение его аргумента находится в 3-й четверти, то главное значение его аргумента 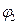 равно равно 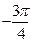 . . | 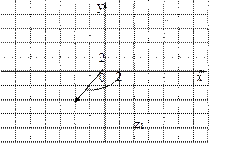 |
Обратите внимание, что если 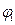 равно
равно 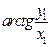 , то
, то 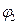 равно
равно 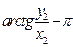 . Добавочное слагаемое
. Добавочное слагаемое 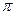 не меняет тангенса аргумента. Оно связано с необходимостью «попасть» в нужную четверть.
не меняет тангенса аргумента. Оно связано с необходимостью «попасть» в нужную четверть.
У числа 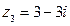 найдем модуль найдем модуль 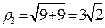 . Тангенс аргумента здесь равен . Тангенс аргумента здесь равен 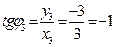 . Соответственно лавное значение его аргумента . Соответственно лавное значение его аргумента 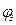 равно равно 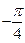 . . | 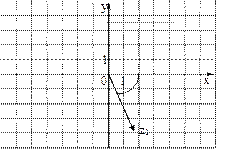 |
Заметим, что 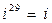 , т.е. модуль и аргумент этого числа равны 1 и
, т.е. модуль и аргумент этого числа равны 1 и 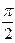 . Теперь найдем
. Теперь найдем 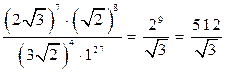 - искомый модуль комплексного числа и одно из значений аргумента
- искомый модуль комплексного числа и одно из значений аргумента 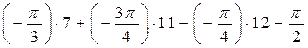 , равное
, равное 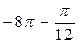 . Отсюда главное значение аргумента равно
. Отсюда главное значение аргумента равно 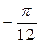 .
.
Ответ. 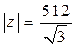 ,
, 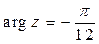
Пример 3. Найдите 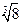 . Решение. На рисунке отмечены 3 точки, которые являются корнями 3-й степени из числа 8. Эти 3 точки находятся на окружности радиуса 2 и имеют аргументы 0, . Решение. На рисунке отмечены 3 точки, которые являются корнями 3-й степени из числа 8. Эти 3 точки находятся на окружности радиуса 2 и имеют аргументы 0, 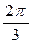 и и 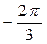 . . | 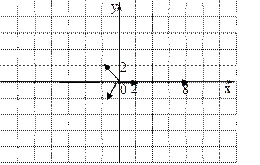 |
Итак, 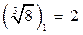 ,
, 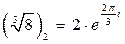 ,
, 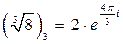 .
.
