Преобразование подобия плоскости. Свойства. Приложение к решению задач

Подобием μ называется такое преобразование плоскости, которое расстояние между любыми двумя точками изменяет в r>0 раз: .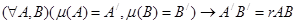

При условии r=1 это движение.

Гомотетия с коэффициентом 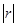также является частным случаем подобия .

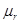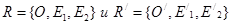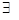Теорема: Если даны прямоугольные декартовы реперы , то единственное подобие μ, которое осуществляет перевод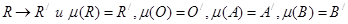

Как и для движений можно показать, что 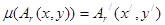и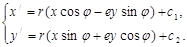

Из этих формул следует, что всякое подобие можно представить в виде произведения гомотетии и движения .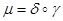

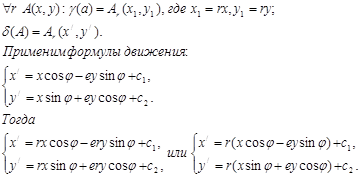
Из теоремы следует, что:

-прямые переходят в прямые,

-углы между линиями сохраняются,

-все расстояния изменяются в r раз.

Теорема: множество преобразований подобия (на плоскости) образуют группу.

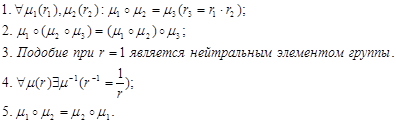
Группу подобия G(μ) называют метрической группой (группой Клейна), которая позволяет измерять расстояния.

Подгруппой является группа движений 1 рода (не изменяет ориентацию фигуры: параллельный перенос, поворот, центральная симметрия и тождественное преобразование).

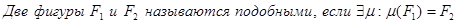
Подобие является частным случаем отношения эквивалентности:

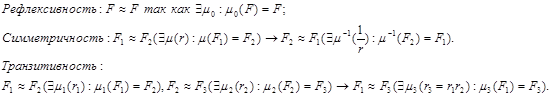
Подобие можно разбить на два класса:

-сохраняет ориентацию – 1 рода (образует группу);

-изменяет ориентацию – 2 рода (не образует группу).

При подобии площади фигур изменяются в r² раз, где r – коэффициент подобия.

Применение к решению задач:

Построить треугольник по двум углам и периметру.

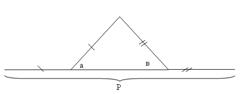
Используем свойство подобия: линейные размеры подобных фигур соотносятся с коэффициентом подобия r.

1.Строим треугольник, у которого:

-основание равно нашему периметру,

-углы при основании равны нашим углам (получим треугольник, подобный данному – согласно 2 признаку подобия);

2. Можно определить новый периметр K, исходный периметр и сторона AB известны.

Так как треугольники подобны, то 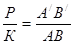. Согласно теореме Фалеса найдем .

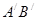Аналогично найдем .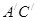

3. Откладываем 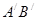от точки 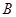и получаем 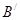, аналогично 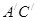от точки 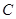и получаем 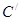. Строим углы a и b, и получаем нужный нам треугольник .

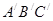. Параллельные прямые на плоскости Лобачевского.

Аксиома: Через точку, лежащую вне прямой в плоскости, определяемой ими, можно провести не менее двух прямых, не пересекающих данной прямой.

Существование хотя бы одной прямой, проходящей через данную точку и не пересекающей данной прямой, есть факт абсолютной геометрии. Аксиома Лобачевского утверждает существование по крайней мере двух таких прямых. Отсюда немедленно следует, что таких прямых существует бесконечное множество.

Плоскость, в которой предполагается выполнение аксиомы Лобачевского, называется плоскостью Лобачевского.

Геометрию Лобачевского называют гиперболической геометрией, в соответствии с чем плоскость и пространство Лобачевского называются гиперболическими.

Теорема: Пусть в плоскости даны прямая a и не лежащая на ней точка A. Тогда в пучке прямых с центром в точке A существуют две пограничные прямые, разделяющие все прямые пучка на два класса: на класс прямых, пересекающих a, и класс прямых, не пересекающих a. Эти граничные прямые сами не пересекают a.

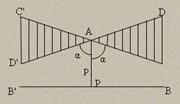
Всё сказанное приводит нас к следующей картине расположения прямых пучка с центром в точке A, взятой вне данной прямой BB'. В этом пучке существуют две граничные прямые CC' и DD', симметрично расположенные относительно перпендикуляра AP, опущенного из точки A на BB', и образующие с ним ےCAP=ےD'AP=α<π/2 .

Эти прямые, а также все прямые пучка, проходящие внутри заштрихованных вертикальных углов CAD и C'AD', не пересекают прямой BB', а все прямые пучка, проходящие внутри вертикальных углов CAD' и C'AD, пересекают BB'.

Две граничные прямые CC' и DD' называются параллельными прямой BB' в точке A, причём прямая C'C называется параллельной B'B в направлении B'B, а прямая DD' называется параллельной прямой BB' в направлении BB'. Острый угол α, образуемый параллельными с перпендикуляром AP, называется углом параллельности в точке A относительно прямой BB'. Этот угол есть функция длины p перпендикуляра AP и обозначается так: α=П(p). AP называется отрезком параллельности в точке A относительно прямой BB'.

Основная формула геометрии Лобачевского, устанавливающая зависимость между длиной отрезка и отвечающим ему углом параллельности, имеет вид: .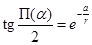

Все прямые пучка, не пересекающие BB' и лежащие внутри заштрихованных вертикальных углов, называются расходящимися с BB' или сверхпараллельными к BB'; угол, образуемый такой прямой с перпендикуляром AP с обеих от него сторон, больше угла параллельности α. Все остальные прямые пучка, образующие с AP с какой-либо стороны острый угол, меньший угла параллельности α, называются пересекающими прямую BB' или сходящимися с BB'.

Прямая C'C называется параллельной прямой B'B в направлении B'B в точке A, если, во-первых, прямая C'C не пересекает прямой BB', во-вторых, C'C является граничной в пучке прямых с центром в точке A, то есть всякий луч AE, проходящий внутри угла CAD, где D – любая точка прямой BB', пересекающей луч DB.

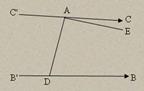
Замечание. Через точку A, лежащую вне прямой BB', можно провести в каждом из двух направлений лишь единственную параллельную Лобачевского к прямой BB', то есть каждому значению длины перпендикуляра p соответствует вполне определённое значение угла параллельности α.

В плоскости Лобачевского две прямые могут либо пересекаться, либо могут быть параллельными в некотором направлении, либо расходящимися. Поэтому в плоскости Лобачевского существует три вида пучков прямых:

1) пучок прямых, пересекающихся в одной точке, называемой центром пучка; такой пучок называется центральным или эллиптическим;

2) пучок прямых, параллельных в заданном направлении некоторой прямой, называемой осью пучка; такой пучок называется параболическим;

3) пучок расходящихся прямых, перпендикулярных к некоторой прямой, называемой базой пучка; такой пучок называется гиперболическим.

Эти три вида пучков связаны с тремя основными кривыми плоскости Лобачевского, являющимися кривыми постоянной кривизны.

Секущей равного наклона к двум данным прямымназывается прямая, которая при пересечении с данными образует равные внутренние односторонние углы.

Если a и b – две прямые пучка и AB – какая-нибудь секущая равного наклона, пересекающая a и b в точках A и B, то эти точки называютсявзаимно соответственными относительно пучка.

Геометрическое место точек, соответственных некоторой точке A, взятой на одной прямой пучка, называется окружностью, орициклом или эквидистантой в зависимости от того, будет ли данный пучок прямых соответственно эллиптическим, параболическим или гиперболическим. Сама точка A также включается в соответствующее геометрическое место.

Прямая, как база гиперболического пучка, является частным случаем эквидистанты.

Орицикл может скользить по себе самому без деформации, подобно тому как это имеет место для прямой и окружности. Таким же свойством обладает и эквидистанта: если заставить скользить по самой себе базу эквидистанты, то и сама эквидистанта будет скользить сама по себе без деформации, ибо расстояния всех точек эквидистанты от базы равны между собой.

Таким образом, в геометрии Лобачевского имеется четыре типа линий постоянной кривизны: прямая, окружность, орицикл и эквидистанта.

В зависимости от того, принадлежат ли три перпендикуляра в серединах сторон треугольника к эллиптическому, гиперболическому или параболическому пучку, около треугольника можно описать либо окружность, либо эквидистанту, либо орицикл, ибо стороны треугольника будут секущими равного наклона относительно соответствующего пучка. В отличие от окружности орицикл и эквидистанта – линии незамкнутые.