Прямые заданы уравненями с угловым коэффициентом
Пусть две прямые 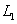 и
и 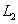 заданы уравнениями с угловым коэффициентом
заданы уравнениями с угловым коэффициентом
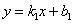 и
и 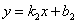 .
.
Если 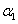 и
и 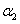 - углы наклона прямых
- углы наклона прямых 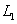 и
и 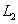 к оси Ox, то из элементарных соображений следует, что
к оси Ox, то из элементарных соображений следует, что
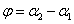 .
.
Таким образом,
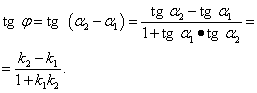
Получаем следующую формулу для определения угла между прямыми:
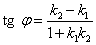 . (3)
. (3)
Пример 3. Найти угол между прямыми, заданными уравнениями с угловым коэффициентом 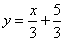 и
и 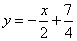 .
.
Решение. По формуле (3) находим:
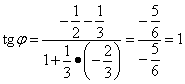 .
.
Искомый угол
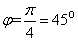
Пусть прямые 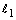 и
и  заданы каноническими уравнениями
заданы каноническими уравнениями 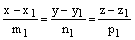 и
и 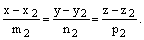 Очевидно, угол между прямыми равен углу между направляющими векторами этих прямых:
Очевидно, угол между прямыми равен углу между направляющими векторами этих прямых: 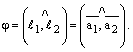 Тогда
Тогда
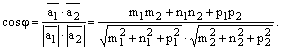 | (2.38) |
Если 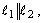 то
то 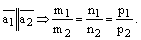
Если 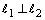 , то
, то 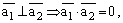 или
или 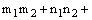
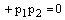 .
.
Геометрический смысл знака трёхчлена Ax + By + C
Если дано общее уравнение некоторой прямой, расположенной в некоторой ПДСК-2, то точки этой прямой и только они обращают это уравнение в верное равенство. Точки же ей не принадлежащие будут очевидно обращать трёхчлен Ax + By + C в некоторое действительное, отличное от нуля число. Это число может быть как положительным, так и отрицательным. Оказывается, что справедливо следующее утверждение. Теорема 8.3. Пусть в некоторой ПДСК-2 некоторая прямая задана своим общим уравнением Ax + By + C = 0. Все точки плоскости, для которых Ax+By+C > 0 лежат в одной полуплоскости относительно данной прямой, а все точки плоскости для которых Ax + By + C < 0 лежат в другой полуплоскости. ◭ Пусть в некоторой ПДСК-2 прямая a задана общим уравнением Ax + By + C = 0 и пусть M(x, y) — некоторая точка этой плоскости. Пусть M0(x0, y0) — основание перпендикуляра, опущенного из точки M на прямую a (рис. 40). Тогда Ax0 + By0 + C = 0. Очевидно, что векторы ~n(A, B) и −−−→ M0M коллинеарны. Следовательно, существует единственное число λ 6= 0 такое, что ~n = λ −−−→ M0M. Тогда, перейдя к координатам, получим: A = λ(x − x0); B = λ(y − y0). Отсюда x = A λ + x0; y = B λ + y0. Следовательно, Ax + By + C = A( A λ + x0) + B( B λ + y0) + C = 51 1 λ (A 2 + B 2 ) + Ax0 + By0 + C = 1 λ (A 2 + B 2 ). Значит, знак трёхчлена Ax+By+C равен знаку 1 λ . Если ~n ↑↑ −−−→ M0M, то λ > 0 и Ax + By + C > 0, если же ~n ↑↓ −−−→ M0M, то λ < 0 и Ax + By + + C < 0. Итак, для любых двух точек, лежащих в одной полуплоскости относительно прямой a, связанные векторы, концами которых являются эти точки, а началами — их проекции на прямую a, будут сонаправлены и поэтому для них знаки трёхчлена Ax + By + C будут одинаковыми, а для двух точек из разных полуплоскостей — разными.
Способы задания плоскости. Взаимное расположение двух и трех плоскостей в пространстве.
плоскость может быть задана:
· проекциями трёх точек, не лежащих на одной прямой (Рисунок 3.1,а);
· проекциями точки и прямой (Рисунок 3.1,б);
· проекциями двух пересекающихся прямых (Рисунок 3.1,в);
· проекциями двух параллельных прямых (Рисунок 3.1,г);
· плоской фигурой (Рисунок 3.1,д);
· следами плоскости;
· линией наибольшего ската плоскости.
Взаимное положение двух плоскостей
