Определенный интеграл. Интегрируемость непрерывной функции. Формула Ньютона – Лейбница
Рассмотрим непрерывную функцию y = f ( x ), заданную на отрезке [ a, b ] и сохраняющую на этом отрезке свой знак ( рис.8 ).
Фигура, ограниченная графиком этой функции, отрезком [ a, b ] и прямыми x = a и x = b, называется криволинейной трапецией.
Для вычисления площадей криволинейных трапеций используется следующая теорема:
Если f – непрерывная, неотрицательная функция на отрезке [a, b], и F – её первообразная на этом отрезке, то площадь соответствующей криволинейной трапеции равна приращению первообразной на отрезке [a, b], т.e.
Рассмотрим функцию S ( x ), заданную на отрезке [ a, b ]. Если a<x 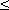 b, то S ( x ) – площадь части криволинейной трапеции, лежащей слева от вертикальной прямой, проходящей через точку ( x, 0 ). Отметим, что если x = a , то S ( a ) = 0, а S ( b ) = S ( S – площадь всей криволинейной трапеции). Можно доказать, что
b, то S ( x ) – площадь части криволинейной трапеции, лежащей слева от вертикальной прямой, проходящей через точку ( x, 0 ). Отметим, что если x = a , то S ( a ) = 0, а S ( b ) = S ( S – площадь всей криволинейной трапеции). Можно доказать, что
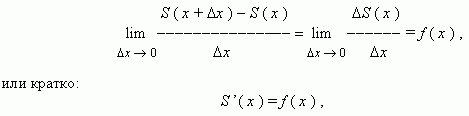
т.e. S ( x ) – первообразная для f ( x ). Отсюда, согласно основному свойству первообразных, для всех x 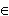 [ a, b ] имеем:
[ a, b ] имеем:
S ( x ) = F ( x ) + C ,
где C – некоторая постоянная, F – одна из первообразных функции f .
Чтобы найти C , подставим x = a :
F ( a ) + C = S ( a ) = 0,
отсюда, C = F ( a ) и S ( x ) = F ( x ) F ( a ). Так как площадь криволинейной трапеции равна S ( b ) , то подставляя x = b , получим:
S = S ( b ) = F ( b ) F ( a ).
П р и м е р . Найти площадь фигуры, ограниченной кривой y = x2 и прямыми
y = 0, x = 1, x = 2 ( рис.9 ) .
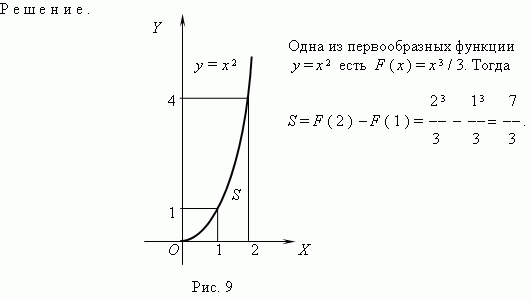
Определённый интеграл. Рассмотрим другой способ вычисления площади криволинейной трапеции. Разделим отрезок [ a, b ] на n отрезков равной длины точками:
x0 = a < x1< x2< x3<…< x n 1< xn = b
и пусть 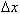 = ( b – a ) / n = xk xk 1, где k= 1, 2, …, n – 1, n .
= ( b – a ) / n = xk xk 1, где k= 1, 2, …, n – 1, n .
В каждом из отрезков [ xk 1, xk ] как на основании построим прямоугольник высотой f ( xk - 1 ). Площадь этого прямоугольника равна:
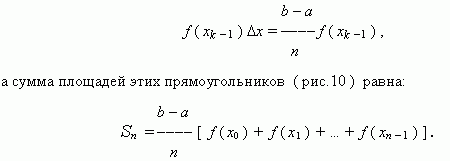
Ввиду непрерывности функции f (x) объединение построенных прямоугольников при большом n ( т.e. при малом 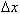 "почти совпадает" с нашей криволинейной трапецией ). Поэтому, Sn
"почти совпадает" с нашей криволинейной трапецией ). Поэтому, Sn 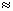 Sпри больших значениях n . Это значит, что Sn
Sпри больших значениях n . Это значит, что Sn 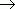 S при n
S при n 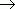
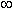 Этот предел называется интегралом функции f ( x ) от a до b или определённым интегралом :
Этот предел называется интегралом функции f ( x ) от a до b или определённым интегралом :

Числа a и b называются пределами интегрирования, f ( x ) dx – подынтегральным выражением.
Итак, если f ( x ) 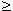 0 на отрезке [ a, b ], то площадь S соответствующей криволинейной трапеции вычисляется по формуле:
0 на отрезке [ a, b ], то площадь S соответствующей криволинейной трапеции вычисляется по формуле:
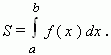
Формула Ньютона - Лейбница. Сравнивая две формулы для площади криволинейной трапеции, приходим к следующему заключению: если F ( x ) - первообразная функции f ( x ) на отрезке [ a, b ], то
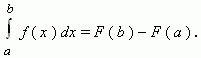
Это и есть знаменитая формула Ньютона – Лейбница.Она справедлива для любой функции f ( x ), непрерывной на отрезке [ a, b ] .
 Р е ш е н и е.
Р е ш е н и е.
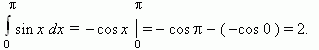
Т е о р е м а 1. Если функция 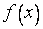 непрерывна на
непрерывна на 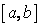 , то она интегрируема на
, то она интегрируема на 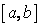 .
.
Д о к а з а т е л ь с т в о. Так как функция 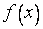 непрерывна на
непрерывна на 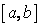 , то она равномерно непрерывна на
, то она равномерно непрерывна на 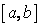 и, следовательно,
и, следовательно, 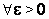
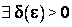 такое, что как только
такое, что как только 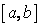 разбит на части с
разбит на части с 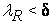 , то все колебания
, то все колебания 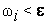 . Отсюда
. Отсюда
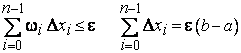 .
.
В силу произвольности 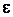 заключаем, что
заключаем, что 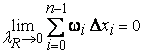 , и по теореме 1 § 6.6 функция
, и по теореме 1 § 6.6 функция 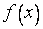 интегрируема.
интегрируема.
