Учет сил трения скольжения во вращательной кинематической паре.

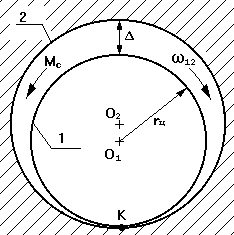
1 - цапфа

r_ц - радиус цапфы

Δ - зазор

r - радиус круга трения;

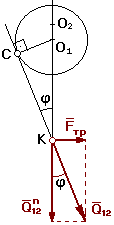
r = О₁С

Рис.5.2

Из ΔО₁СК à 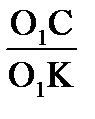= sin j à О₁С = О₁К sin j

M_c= Q₁₂^.О₁С = Q₁₂^. r_ц^.sin j

При малых углах j sin j ≈ tg j = f .

Тогда :

M_c= Q₁₂^. r_ц^.f

При учете трения во вращательной КП результирующая реакция отклоняется

от общей нормали на угол трения j и проходит касательно к кругу трения радиуса r.

Трение качения- трение движения двух твёрдых тел , при котором их скорости в точках касания одинаковы по величине и направлению.

Вследствие контактных деформаций трение качения сопровождается неизбежным скольжением и рассеянием энергии в результате внутреннего трения.

Для расчёта силы трения используется формула Кулона. При качении цилиндра (сферы) по плоскости ( рис.5.3)

F_f= k*F_n/R , где k- коэффициент трения качения;

F_n- cила, с которой цилиндр прижат к плоскости;

R – радиус цилиндра (сферы).

Коэффициент трения качения ( мм.) - берётся из справочников и зависит от твёрдости контактирующих поверхностей.

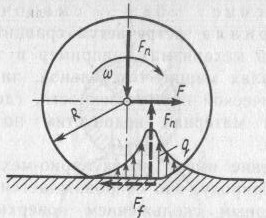
Рис.5.3

Методикасилового расчета рычажного механизма.

Рассмотрим аналитический метод силового анализа на примере схемы кривошипно-ползунного механизма (рис.5.4). Здесь же показаны все приложенные силы и моменты. При силовом расчете должны быть заданы (в метрах): радиус кривошипа 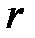, длина шатуна 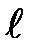. Положение центров масс звеньев определяется расстояниями , , .

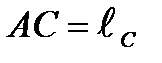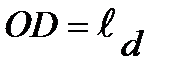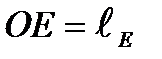Задается средняя угловая скорость кривошипа .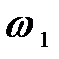

Считаются известными: масса кривошипа 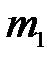(кг), масса шатуна 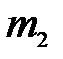(кг),

масса ползуна 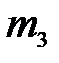(кг), масса противовеса 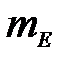(кг), момент инерции шатуна относительно центра массы 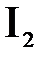(кгм²).момент инерции вращающихся масс на валу кривошипа 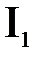(кгм²).

Положение механизма на плоскости определяется углом 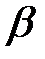между положительным направлением оси Х и вектором силы тяжести (отсчитывается от оси Х против часовой стрелки).

Угол 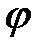отсчитывается от положения кривошипа 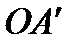, в котором ползун занимает крайнее дальнее положение .

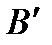Во всех положениях механизма задается величина углового ускорения кривошипа 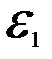(с^-2). Его величина определяется в результате динамического анализа машины .

Отсчет угла 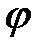, направление угловой скорости 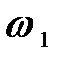и углового ускорения 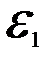против часовой стрелки считаются положительными.

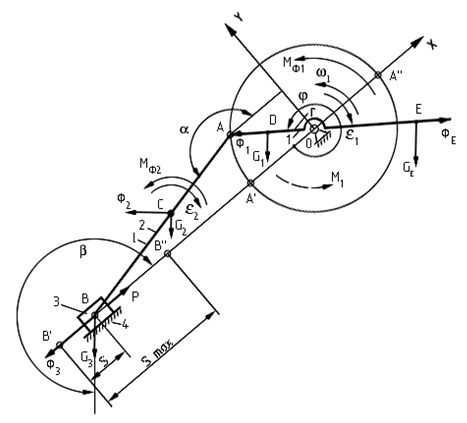
Рис.5.4

К ползуну приложена внешняя сила P (Н). Её величина задается в каждом положении механизма и является положительной, если ее направление совпадает с осью Х.

Силы трения в кинематических парах не учитываются.

На кривошипе должен быть приложен уравновешивающий момент 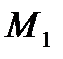(Нм), величина и направление которого определяются в каждом положении.

Определяются силы тяжести звеньев:

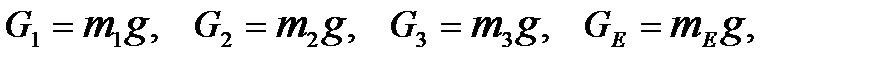(5.1)

где g=9,8 м/с² .

Исследование ведется по методу кинетостатики [1]. К движущемуся механизму применяются уравнения равновесия статики, но в рассмотрение вводятся инерционные нагрузки (принцип Даламбера) .

Силы инерции звеньев:

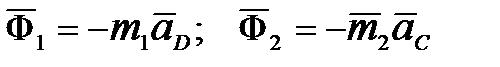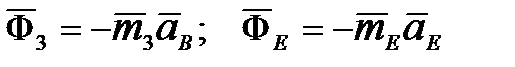; . (5.2)

Здесь и далее не учитываются касательные составляющие сил инерци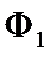и и 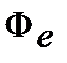, возникающие при движении кривошипа с ускорением.

Инерционные моменты кривошипа и шатуна:

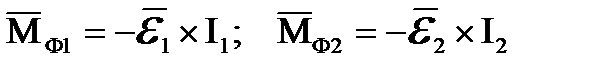. (5.3)

Величины ускорений центров масс звеньев 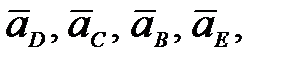величины угловых ускорений кривошипа 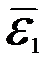, шатуна 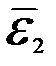определяются при кинематическом и динамическом анализе хода машины.

Для нахождения реакций в кинематических парах нужно выделить из механизма статически определимую группу звеньев, в которой число неизвестных реакций равно числу уравнений кинетостатики (три уравнения).

Например, в начале расчётов нельзя рассматривать равновесие шатуна 2, так как в шарнирах А и В неизвестны по величине и направлению реакции со стороны кривошипа R₁₂ и ползуна R₃₂.

В данном случае, рассматриваем равновесие статически определимой структурной группы “шатун-ползун” (рис.5.5).

Рис.5.5

Векторное уравнение равновесия сил:

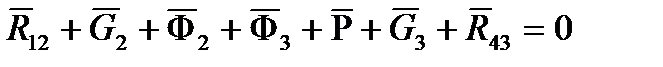. (5.4)

Здесь 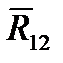и 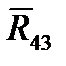— реакции со стороны “отброшенных” звеньев 1 и 4 соответственно на звенья 2 и 3. При этом считаем, что положительное направление 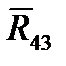совпадает с осью Y.

Проектируя уравнения (5.4) на ось X и используя при этом зависимости (5.1), (5.2),получим:

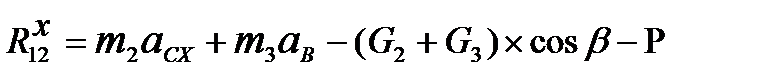. (5.5)

Здесь 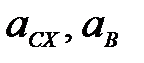определяются по зависимостям (3.22) и (3.21).

Уравнение равновесия моментов всех сил относительно, например, точки A:

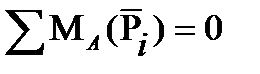. (5.6)

Это уравнение, выраженное через проекции векторов на оси координат X,Y, имеет вид:

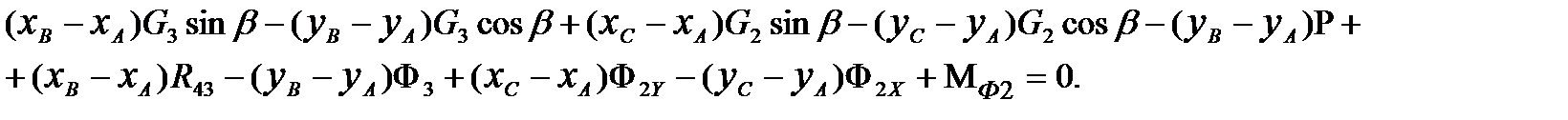
Величины 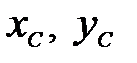определяются по зависимостям (3.6). Координаты 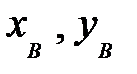и 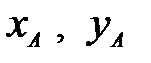можно вычислить по тем же зависимостям (3.6), подставляя вместо 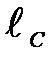соответственно 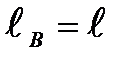и .

И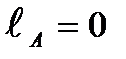спользуя зависимости (5.1), (5.2), (5.3), после преобразований получаем:

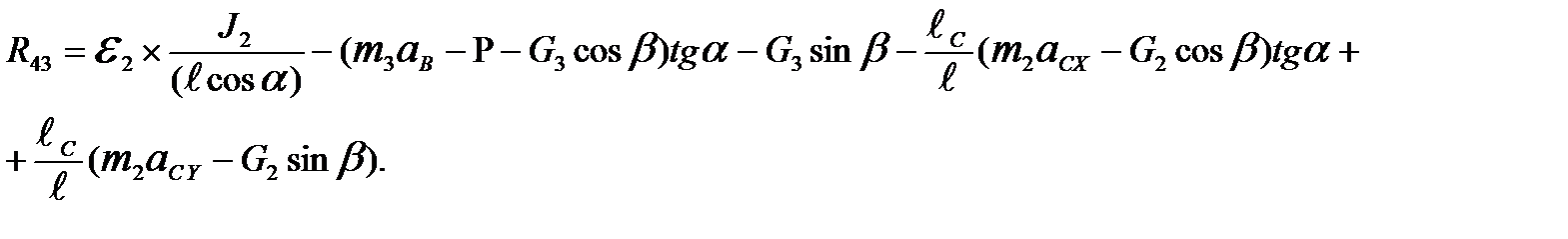
(5.7)

Проектируя уравнение (5.4) на ось Y системы координат и используя при этом зависимости (5.1), (5.2), получим:

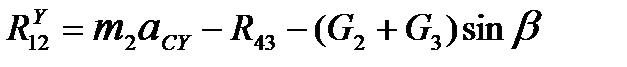. (5.8)

Определим реакцию 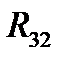в шарнире 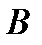. Условие равновесия шатуна запишется в виде: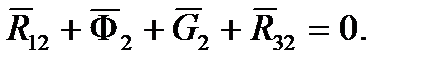

Проектируя данное векторное уравнение на оси X,Y, получим:

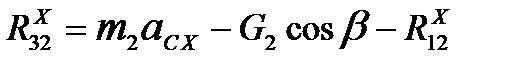, (5.8) .

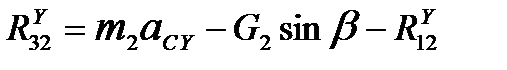Для определения реакции 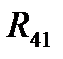в шарнире О и величины уравновешивающего момента 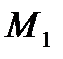рассмотрим равновесие кривошипа 1 (рис.5.6)

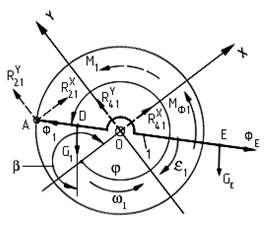
Рис.5.6

Векторное уравнение равновесия сил на кривошипе:

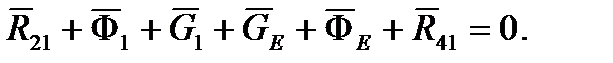(5.9)

Проектируя уравнение (5.9) на оси X,Y системы координат с использованием зависимостей (5.1), (5.2) и учитывая, что 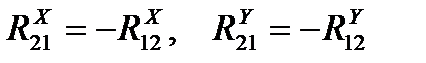, получаем:

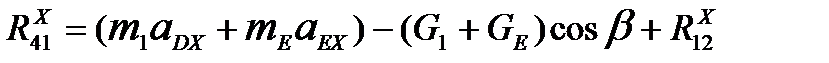, (5.10)

.

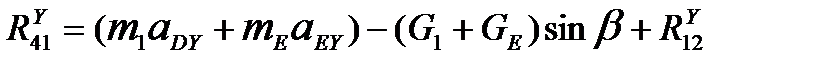Так как точки А, Е, D кривошипа находятся на одной линии, проекции центростремительных ускорений определяются по формулам:

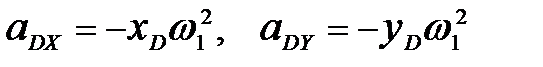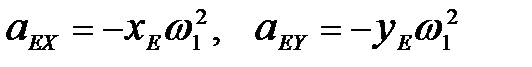; , (5.11) где, 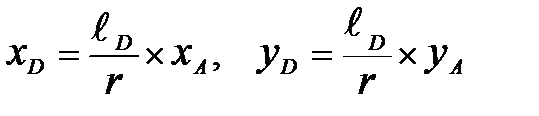; 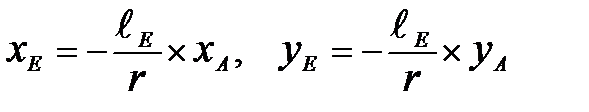. (5.12)

Уравнение равновесия моментов всех сил относительно точки О, выраженное через проекции векторов на оси X,Y, после преобразований имеет вид:

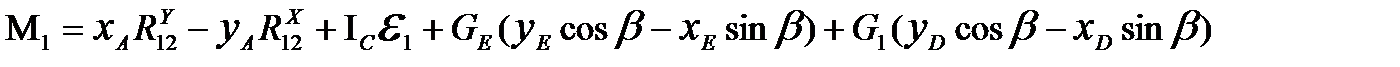. (5.13)

Вышеприведённые расчеты кинематических и силовых величин целесообразно производить с применением компьютерной техники. При выполнении курсовой работы по ТММ студентам выдается более простой вариант задания, позволяющий использовать лишь инженерный калькулятор.

Расчет перемещений, аналогов скоростей и ускорений ползуна можно вести по приближенным зависимостям (3.13-3. 15).

При силовом расчете учитываются лишь наиболее значимые нагрузки, приложенные на ползуне:

а) сила сопротивления P на ползуне, направленная против его скорости ;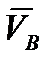

б) сила тяжести ползуна ;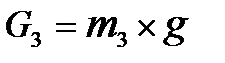

в) сила инерции .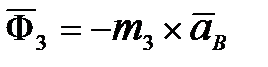

Угловая скорость кривошипа 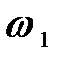считаетсяпостоянной ( ).

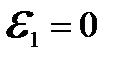В этом случае все полученные зависимости значительно упрощаются. Приведем их для двух наиболее распространенных вариантов расположения схемы механизма.