Интерполяционный многочлен, представленный в виде
Лабораторная работа №1
Проверка адекватности моделей: интерполяция и аппроксимация
Краткие теоретические сведения
Наиболее удобной в обращении на практике функцией является алгебраический многочлен. Чтобы задать многочлен, нужно задать только конечное число его коэффициентов. Значения многочлена легко вычисляются, его легко продифференцировать, проинтегрировать и т.д. Поэтому алгебраические многочлены нашли широкое применение для приближения (аппроксимации) функций. Наряду с алгебраическими многочленами применяются также тригонометрические многочлены, которые являются более естественными для приближения периодических функций.
1.1. Интерполяция функций по формуле Лaгpанжа
Пусть известны значения некоторой функции f в n+1 различных точках х0, х1,…, хn, которые обозначим следующим образом:
fi=f(xi), i=0, 1, …, n.
Например, эти значения получены из эксперимента или найдены с помощью достаточно сложных вычислений. Возникает задача приближенного восстановления функции f в произвольной точке х. Часто для решения этой задачи строится алгебраический многочлен Ln(x) степени n, который в точкаххi принимает заданные значения, т.е.
Ln(xi)=fi, i=0, 1, …, n, (1)
и называется интерполяционным. Точки xi, i=0, 1, …, n называются узлами интерполяции.
Приближенное восстановление функции f по формуле
f(x)»Ln(x)(2)
называется интерполяцией функции f с помощью алгебраического многочлена. Существует теорема, согласно которой имеется только один интерполяционный многочлен n-ой степени, удовлетворяющий условию (1).
Интерполяционный многочлен, представленный в виде
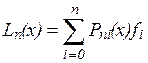 , (3)
, (3)
где
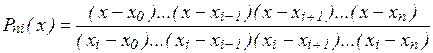 , (4)
, (4)
называется интерполяционным многочленом Лагранжа, а функции (4) – Лагранжевыми коэффициентами.
Погрешность интерполяции (экстраполяции) в текущей точке 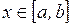 оценивается по формуле
оценивается по формуле
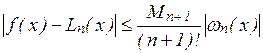 , (5)
, (5)
где
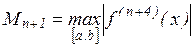 , (6)
, (6)
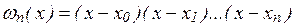 , (7)
, (7)
Максимальная погрешность интерполяции на всем отрезке [a, b]:
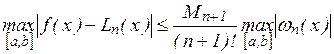 . (8)
. (8)
1.1.1 Линейная интерполяция
Интерполяция по формуле (2) при n=1, т.е. с помощью линейной функции (3) называется линейной.
Если ввести обозначения h=x1-x0, q=(x-x0)/h, то формула линейной интерполяции может быть записана в следующем виде:
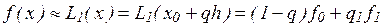 . (9)
. (9)
Величина q называется фазой интерполяции, которая изменяется в пределах от 0 до 1, когда х пробегает значение от х0 до х1.
Геометрическая линейная интерполяция означает замену графика функции на отрезке [x0, x1] хордой, соединяющей точки (х0, f0), (х1, f1), как показано на нижеприведенном рисунке.
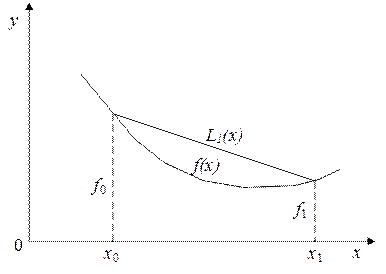
1.2 Сплайны
Пусть отрезок [a, b] разбит на N равных частичных отрезков [xi, xi+1], где xi=a+ih, i=0, 1, …, N-1; xN=b, h=(b-q)/N.
Сплайном называется функция, которая вместе с несколькими производными непрерывна на всем заданном отрезке [a, b], а на каждом частичном отрезке [xi, xi+1] в отдельности является некоторым алгебраическим многочленом.
Максимальная по всем частичным отрезкам степень многочленов называется степенью сплайна, а разность между степенью сплайна и порядком наивысшей непрерывной на [a, b] производной – дефектом сплайна.
На практике наиболее широкое распространение получили кубические сплайны – сплайны третьей степени, имеющие на [a, b] непрерывную, по крайне мере, первую производную. Величина 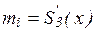 называется наклоном сплайна в точке (узле) хi.
называется наклоном сплайна в точке (узле) хi.
Нетрудно убедится, что кубический сплайн S3(x), принимающий в узлах xi, xi+1, соответственно значения fi, fi+1, имеет на частичном отрезке [xi, xi+1] вид
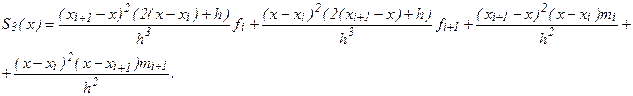 (10)
(10)
Действительно, легко видеть, что S3(xi)=fi, S3(xi+1)=fi+1. Кроме того, простые вычисления показывают, что 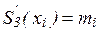 ,
, 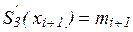 . Можно доказать, что любой алгебраический многочлен третьей степени, принимающий в точках xi, xi+1 значения, равные соответственно fi, fi+1 и имеющий в этих точках производную, соответственно равную mi, mi+1, тождественно совпадает с многочленом (10).
. Можно доказать, что любой алгебраический многочлен третьей степени, принимающий в точках xi, xi+1 значения, равные соответственно fi, fi+1 и имеющий в этих точках производную, соответственно равную mi, mi+1, тождественно совпадает с многочленом (10).
Итак, чтобы задать кубический сплайн S3(x) на всем отрезке [a, b], нужно задать в N+1 узлах xi его значения fi и наклоны или касательные mi, i=0, 1, …, N.
Кубический сплайн, принимающий в узлах xi те же значения, что и некоторая функция f называется интерполяционным. Он служит для аппроксимации функции f на отрезке [a, b] вместе с несколькими производными.
Способы задания наклонов интерполяционного кубического сплайна.
1) Упрощенный способ
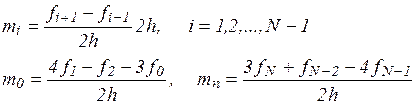 (11)
(11)
2) Если известны значения 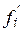 производной
производной 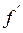 в узлах xi, то полагаем mi=
в узлах xi, то полагаем mi= 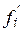 , i=0, 1, …, N.
, i=0, 1, …, N.
Способы 1 и 2 – локальные, так как с их помощью сплайн строится отдельно на каждом частичном отрезке [xi, xi+1].
3) Глобальный способ.
Обозначаем через 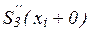 значение
значение 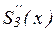 в узле xi справа, найденное непосредственно из выражения (10), а через
в узле xi справа, найденное непосредственно из выражения (10), а через 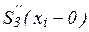 значение
значение 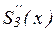 в узле xi слева, т.е. найденное из соответствующего выражения
в узле xi слева, т.е. найденное из соответствующего выражения 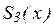 на частичном отрезке [xi-1, xi], которое получается из (10) заменой i на i-1.
на частичном отрезке [xi-1, xi], которое получается из (10) заменой i на i-1.
Имеем
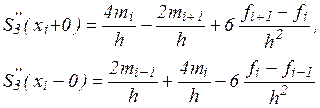
Требуем непрерывности S”(x) в узлах:
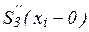 =
= 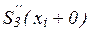 , i=1, 2, …, N-1
, i=1, 2, …, N-1
и приходим к следующей системе линейных алгебраических уравнений относительно наклонов:
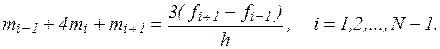 (12)
(12)
Поскольку неизвестных N+1, то необходимо задать еще два условия, которые называются краевыми (они обычно связаны с крайними значениями m0 и mN). Дадим три варианта краевых условий:
а) Если известны 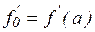 ,
, 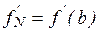 , то задать m0=
, то задать m0= 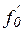 , mN=
, mN= 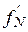 .
.
б) Производные 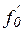 и
и 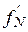 аппроксимируем формулами численного дифференцирования третьего порядка точности:
аппроксимируем формулами численного дифференцирования третьего порядка точности:
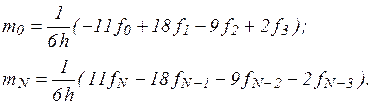 (13)
(13)
в) В некоторых случаях бывают известны значения f ’’ на концах отрезка [a, b], т.е. величины 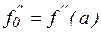 ,
, 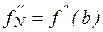 . Тогда требование
. Тогда требование 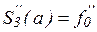 ,
, 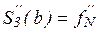 приводит к краевым условиям:
приводит к краевым условиям:
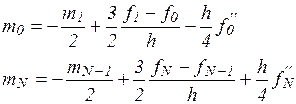 (14)
(14)
Система (12) при всех рассматриваемых краевых условиях имеет единственное решение. Решая систему (12) при выбранных краевых условиях, находим наклоны mi, i=0, 1, …, N, во всех узлах. Затем по формуле (10) задаем сплайн на каждом частичном отрезке [xi, xi+1], i=0,1,…,N-1.
Построенный данным глобальным способом сплайн S3(х) имеет дефект не больше единицы, т.к. этот сплайн обладает на отрезке [a, b] непрерывной второй производной.
Интерполяционный сплайн S3(х) с наклоном, заданным способом 2 или 3, удовлетворяет неравенству
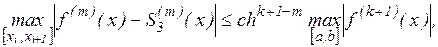 (15)
(15)
где 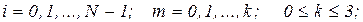 с - независящая от h, i, f постоянная.
с - независящая от h, i, f постоянная.
Точность аппроксимации функции f сплайном S3(х) управляется выбором N, т.е. шагом h=(b-a)/N.
1.3. Аппроксимация функций по методу наименьших квадратов
Интерполяция на практике хороша лишь для таких функций, значения которых не искажены шумом. Случайные ошибки в значениях функции сильно искажают интерполяционное многочлены высоких степеней, а при интерполяции многочленами низких степеней теряется существенная информация. Поэтому, в этом случае, целесообразно применять «сглаживающую» аппроксимацию с минимизацией взвешенной средней квадратической ошибки аппроксимации. Это значит, что для данной функции f(х) требуется построить функцию F(х) вида
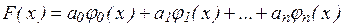 (16)
(16)
так, чтобы минимизировать взвешенную среднюю квадратическую ошибку на интервале [a, b]:
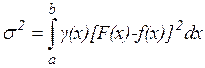 (17)
(17)
где g(х) – заданная весовая неотрицательная функция.
Если функции j(x) действительны и попарно ортогональны с весом g(х) на интервале [a, b], то есть если
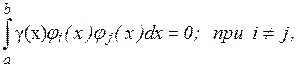 (18)
(18)
то искомые коэффициенты определяются по формуле
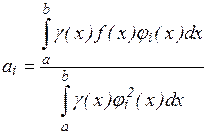
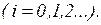
 |
(19)
Аппроксимация ортогональными функциями, например, ортогональными многочленами или тригонометрическими полиномами имеет то замечательное преимущество, что улучшение аппроксимации путем добавления нового члена an+1 jn+1 (x) не меняет ранее вычисленные коэффициенты а0, а1, а2, …,аn.
Таким образом, для аппроксимации функции f(х) необходимо задать класс приближающих функций или n-мерное пространство, где n - число заданных значений функции f(х), и норму в этом пространстве. При приближении функций многочленами на дискретном множестве точек норма имеет вид:
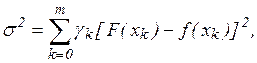 (20)
(20)
где gk заданные положительные веса, m + 1 - дискретное множество точек.
Согласно условию ортогональности (18):
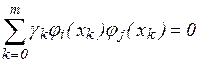
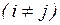 (21)
(21)
и на основании (19) имеем:
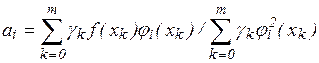
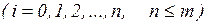 (22)
(22)
Отметим, что можно использовать другую норму (20), тогда получим другое приближение, которое может значительно отличатся от предыдущего.
Приведем пример аппроксимации функций тригонометрическим многочленом:
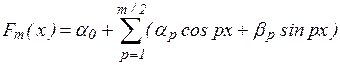 (23)
(23)
Коэффициенты этого многочлена при учете условия (20) находятся согласно формулам:
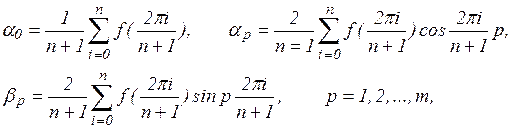 (24)
(24)
где 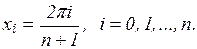
Цель работы.
Получить практические навыки интерполяции и аппроксимации кривых аппроксимирующими многочленами и оценки точности полученных моделей.
Содержание работы и порядок ее выполнения
1. Согласно своему варианту из таблицы 1 в графе 2 выбрать вид исходной функции f(х).
2. Определив из таблицы 1 графа 3 отрезок аппроксимации, определить восемь значений функции f(х) на этом отрезке. Шаг табулирования функции выбрать равномерным, т.е. h=(b-a)/7.
3. Выбрать графы 4 таблицы 1 метод интерполяции, определить интерполяционный полином, проходящий через узлы интерполяции, найденный в п. 2.
4. Протабулировать исходную функцию и найденный интерполяционный полином с шагом h/10. Построить полученные графики. Оценить погрешность приближения.
5. Из таблицы 1 графа 5 определить класс аппроксимирующего многочлена.
6. Используя выражение (22) и данные, приведенные в таблице 2, определить наилучшее приближение функции f(х) на заданном отрезке по методу наименьших квадратов.
7. Протабулировать полученный в п. 6 многочлен с шагом h/7. Построить его график и сравнить с графиком, полученным в п. 4.
Таблица 1
| № п/п | Исходная функция | Отрезок аппроксимации | Метод интерполяции | Класс аппроксимирующих многочленов |
| ех | [-0,5; 0] | Лагранжа | Чебышева | |
| lgx – (x-1)/x | [1; 10] | Линейная | Эрмита | |
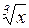 | [1; 1000] | Лагранжа | Лагерра | |
| arc tg x | [0; 1] | Локальный кубический сплайн | Чебышева | |
| sin 3x | [0; p/6] | Локальный кубический сплайн | Лежандра | |
| 1/x | [1; 2] | Линейная | Лагерра | |
| 1/(x2+1) | [0; 1] | Лагранжа | Чебышева | |
| 4x3-3x | [-1;1] | Локальный кубический сплайн | Лежандра | |
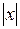 | [-1; 1] | Лагранжа | Лежандра | |
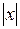 | [-p; p] | Локальный кубический сплайн | Гармоническ. | |
| x | [-p; p] | Линейная | Гармоническ. | |
| x2 | [-p; p] | Глобальный кубический сплайн | Гармоническ. | |
| x2/(p-х) | [0; p] | Лагранжа | Гармоническ. | |
| ех | [0; p] | Линейная | Гармоническ. | |
| 1/(х2-1) | [1; 2] | Локальный кубический сплайн | Эрмита |
Таблица 2
| № п/п | Ортогональные многочлены | Вес 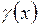 | Интервал ортогонализации | Явное выражение 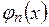 |
| Лежандра | [-1; 1] | 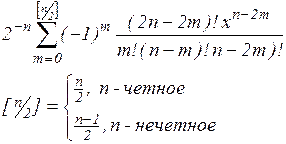 | ||
| Чебышева | 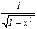 | [-1; 1] | 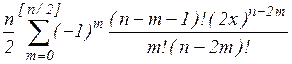 | |
| Лагерра | е-х | [0; ¥] | 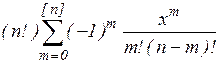 | |
| Эрмита | 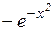 | [-¥; ¥] | 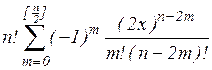 | |
| Гармонические | [-p; p] | {cos nx, sin nx } 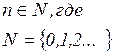 |
