Дифференциальные уравнения
1. Задачи, приводящие к понятию дифференциальных уравнений. Дифференциальные уравнения 1 порядка: определение, общее и частное решение. Начальные условия. Геометрическая трактовка. Порядок, степень дифференциальных уравнений.
2. Понятие о задаче Коши. Теорема существований и единственности.
3. Уравнения с разделенными и разделяющимися переменными.
4. Уравнения однородные относительно Х и У.
5. Линейные дифференциальные уравнения 1 порядка: однородные и неоднородные (метод замены переменной и вариации произвольной постоянной).
6. Уравнение Бернулли.
7. Дифференциальные уравнения высших порядков. Общие понятия. Уравнения, допускающие понижение порядка: 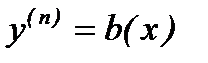 ,
, 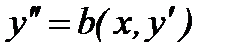 ,
, 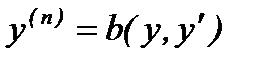 .
.
8. Однородные линейные уравнения 2 порядка. Структура общего решения. Линейно независимые решения. Определитель Вронского. Теорема об определителе Вронского.
9. Линейные неоднородные дифференциальные уравнения 2 порядка. Структура общего решения.
10. Линейные неоднородные дифференциальные уравнения 2 порядка: 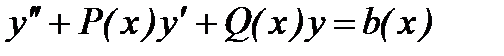 , где
, где 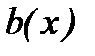 - произвольная функция. Метод вариации произвольной постоянной.
- произвольная функция. Метод вариации произвольной постоянной.
11. Линейные дифференциальные уравнения 2 порядка с постоянными коэффициентами, однородные. Характеристическое уравнение. Определение общего решения, если:
- корни характеристического уравнения действительные различные,
- корни характеристического уравнения действительные корни характеристического уравнения действительные равные,
- корни характеристического уравнения действительные комплексно-сопряженные.
12. Неоднородные линейные дифференциальные уравнения 2 порядка с постоянными коэффициентами: 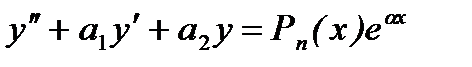 . Нахождение частного и общего решения.
. Нахождение частного и общего решения.
13. Неоднородные линейные дифференциальные уравнения 2 порядка с постоянными коэффициентами: 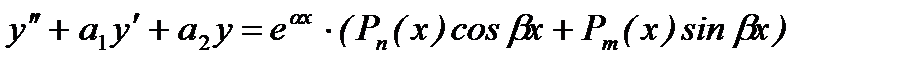 . Нахождение частного решения.
. Нахождение частного решения.
14. Линейные уравнения высших порядков. Метод вариации.
15. Система дифференциальных уравнений с постоянными коэффициентами. Определение, решение нормальной системы.
Ряды
1. Понятие числового ряда, сумма ряда. Сходящиеся и расходящиеся ряды.
2. Геометрическая прогрессия. Выяснить поведение ряда при различных значениях знаменателя прогрессии.
3. Теорема о свойствах числового ряда (отбрасывание членов ряда, суммирование рядов, умножение на постоянный множитель).
4. Необходимое условие сходимости ряда. гармонический ряд.
5. Теоремы сравнения.
6. Признак Даламбера.
7. Интегральный признак Коши.
8. Знакочередующиеся ряды. Теорема Лейбница.
9. Ряды с произвольными членами. Условная и абсолютная сходимость. Теорема (достаточный признак сходимости знакопеременного ряда).
10. Функциональные ряды. Точки сходимости ряда. Область сходимости.
11. Теорема об интегрировании и дифференцировании равномерно-сходящихся рядов.
12. Степенные ряды. Теорема Абеля.
13. Радиус и интервал сходимости степенного ряда. Теорема об определении радиуса сходимости степенного ряда.
14. Свойства степенных рядов (без доказательства).
15. Ряд Тейлора и Маклорена. Необходимое и достаточное условия для разложения функции в ряд Тейлора.
16. Разложение в ряд Маклорена функции вида: 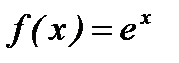 ,
, 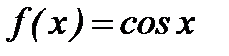 ,
, 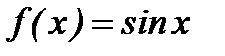 .
.
17. Биномиальный ряд.
18. Разложение в ряд функции: 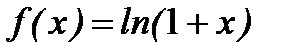 ,
, 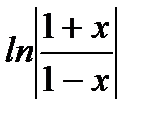 ,
, 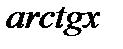 .
.
19. Приближенное вычисление значений функции. Оценка ошибки.
20. Вычисление определенных интегралов с помощью рядов.
