Метод Рунге - Кутта 1-го порядка (метод Эйлера)
Отбросим члены ряда, содержащие h2, h3, h4:.
Тогда 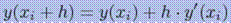 .так как
.так как 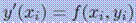
Получим формулу Эйлера:
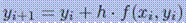 |
Точность метода Эйлера на каждом шаге составляет 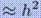 .
.
Основной недостаток метода Эйлера - систематическое накопление ошибок. Поэтому его рекомендуется применять для при малых значениях шага интегрирования h.
Реализуем этот метод на C#. Сначала реализуем абстрактный класс, который будет использован для конструирования различных методов построения численных решений систем обыкновенных дифференциальных уравнений.
public abstract class TODE {
private int n;//размерность системы
private double t;// текущее время
private double[] y;// искомое решение y[0] – само решение,
// Y[i] - i-ая производная решения
public double T
{get{return t;}
set{t=value;}}
public int N
{get{return n;}
set{n=value;}}
public double [] Y
{get{return y;}
set{y=value;}}
protected double[] YY; // внутренние переменные
public TODE(int nn)
{N = nn;
YY = new double [N]; Y = new double [N]; }
// установить начальные условия.
// t0 - начальное время, Y0 - начальное условие
public void Setlnit(double tO, double[] Y0)
{T = tO; int i;
for (i = 0; i < N; i++) {Y[i] = Y0[i] ;}}
abstract public void F(double t, double [] Y, ref double[] FY); // правые части системы.
// следующий шаг, dt - шаг по времени
abstract public void NextStep(double dt);}
На основе этого класса построим класс, реализующий метод Эйлера.
public abstract class TEuler : TODE
{public TEuler(int N) : base(N) { }
public override void NextStep(double dt)
{int i;F(T, Y, ref YY);
for (i = 0; i < N; i++) {
Y[i] = Y[i] + dt * YY[i];}
T = T + dt; } }
Метод Рунге - Кутта 2-го порядка (модифицированный метод Эйлера)
Отбросим в члены ряда, содержащие h3, h4, h5:.
Тогда
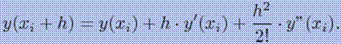 |
Чтобы сохранить член ряда, содержащий h2, надо определить вторую производную y"(xi).Ее можно аппроксимировать разделенной разностью 2-го порядка
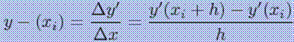
Подставляя это выражение, получим
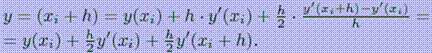
Окончательно, модифицированная формула Эйлера имеет вид:
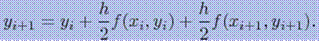 |
Как видно, для определения функции y(x) в точке i+1 необходимо знать значение правой части дифференциального уравнения f(xi+1, yi+1) в этой точке, для определения которой необходимо знать предварительное значение yi+1.
Для определения предварительного значения yi+1 воспользуемся формулой Эйлера. Тогда все вычисления на каждом шаге по модифицированной или уточненной формуле Эйлера будем выполнять в два этапа:
На первом этапе вычисляем предварительное значение 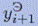 по формуле Эйлера
по формуле Эйлера
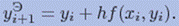
На втором этапе уточняем значение y=i+1 по модифицированной формуле Эйлера
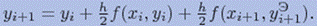
Точность модифицированного метода Эйлера на каждом шаге 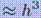 .
.
