Задачи для самостоятельного решения

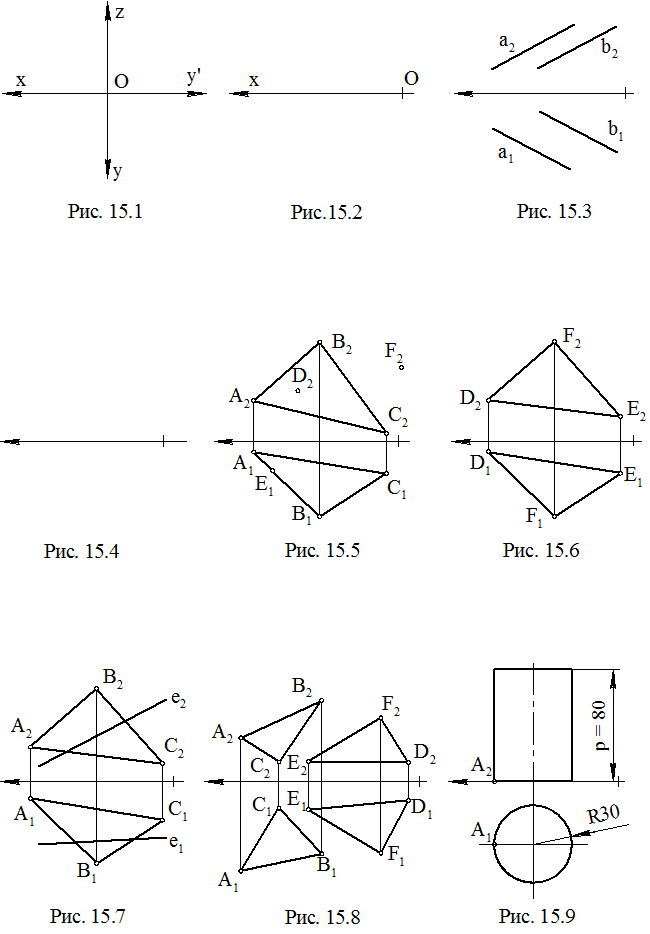
1. Построить КЧ (П₁П₂П₃) точек А(30; 40; 20), В(60; – 40; – 30) (рис. 15.1).

2. Дана точка А(70; 60; 30). Построить точку В, симметричную точке А относительно П₁ (рис. 15.2).

3. Даны прямые a // b общего положения. Построить прямую h // П₁, пересекающую a и b и удаленную от П₁ на 30 миллиметров (рис. 15.3).

4. Даны А(90; 40; 30), В(10; 15; 20), С(60; 45; 20), D(30; 15; 40). Построить прямые (АВ) и (CD). Записать координаты конкурирующих точек (рис. 15.4).

5. Дана плоскость (DАВС), проекции D₂, E₁, F₂. Построить проекции D₁, E₂, F₁, если D, E, F принадлежат плоскости (DАВС) (рис. 15.5).

6. Дана плоскость (DDFE). Через точку D провести горизонталь h, через точку F – фронталь f в этой плоскости (рис. 15.6).

7. Построить точку пересечения прямой e и плоскости (DАВС), указать видимость (рис. 15.7).

8. Построить линию пересечения плоскостей (DАВС) и (DDFE) (рис. 15.8).

9. Построить КЧ правой винтовой линии, расположенной на цилиндре и проходящей через точку А (один виток), шаг винтовой лини равен 80 миллиметров (рис. 15.9).

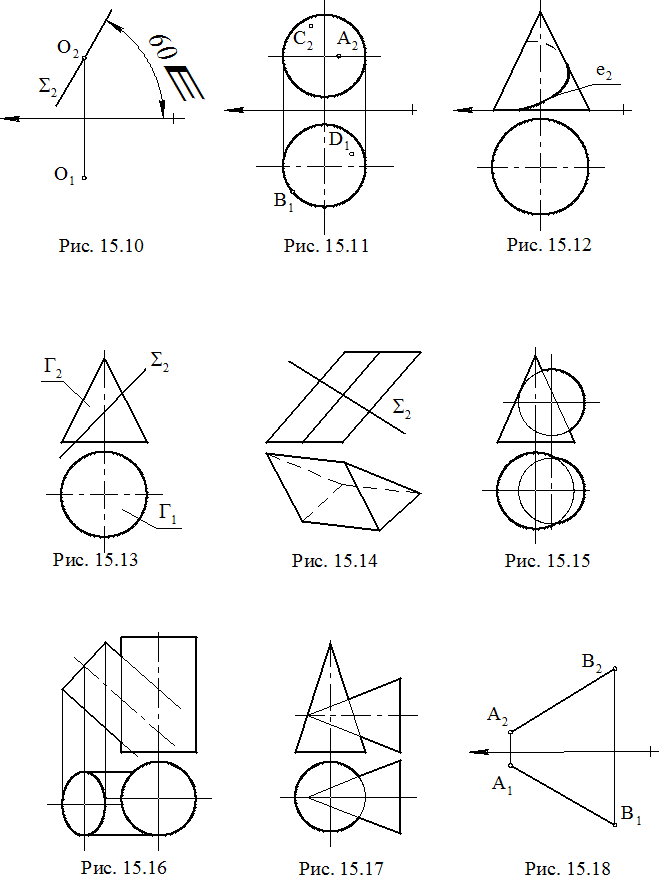
10. Построить проекции окружности R40, с центром О, принадлежащей плоскости S (рис. 15.10).

11. Построить вторые проекции точек, принадлежащих сфере (рис. 15.11).

12. Построить вторую проекцию линии, принадлежащей конической поверхности (рис. 15.12).

13. Построить линию пересечения плоскости S и конической поверхности G (рис. 15.13).

14. Построить линию пересечения призмы и проецирующей плоскости S (рис. 15.14).

15. Построить линию пересечения поверхностей: а) рис. 15.15, б) рис.15.16, в) рис. 15.17.

16. Определить натуральную величину (НВ) отрезка и угол его наклона к плоскости П₁ (рис. 15.18).

17. Определить угол между прямой и плоскостью (рис. 15.7).

18. Определить угол между плоскостями (рис. 15.8).

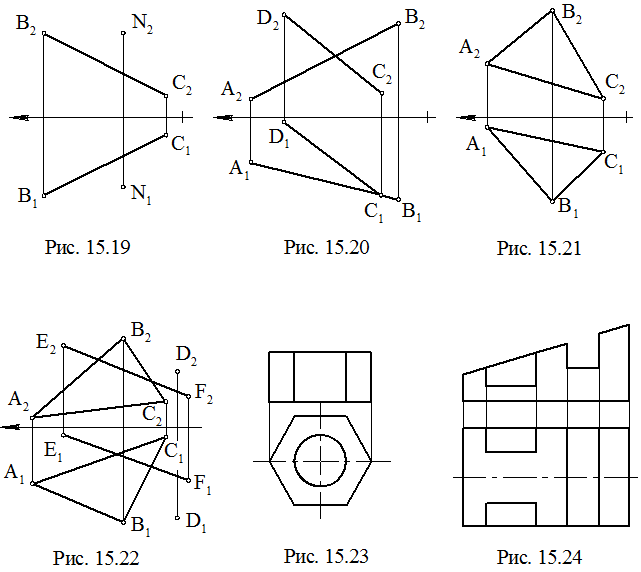
19. Определить расстояние от точки N до прямой (ВС) (рис. 15.19).

20. Определить угол и расстояние между данными прямыми (рис. 15.20).

21. Определить НВ (DАВС) и построить центр вписанной окружности (рис. 15.21).

22. Через точку D провести прямую параллельную плоскости (DАВС), и пересекающую прямую EF (рис. 15.22).

23. Построить изометрию фигуры (рис. 15.23).

24. Построить диметрию фигуры (рис. 15.24).

25. Достроить на П₁ проекцию плоского пятиугольника ABEFC, если A(50; 10; 15), B(25; 0; 0), C(30; 30; 30), E(10; …; 5), F(5; …; 15).

26. Построить прямую t, параллельную прямой (EF) и пересекающую прямые (AB) и (CD), если A(80; 10; 5), B(50; 20; 25), C(65; 30; 30), D(40; 20; 5), E(30; 5; 15), F(5; 30; 15).

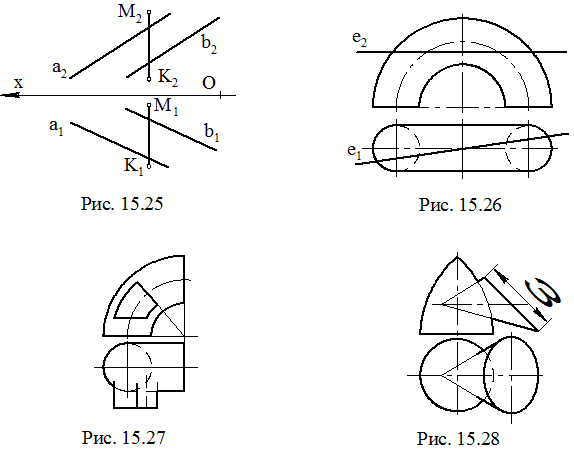
27. Найти точку пересечения плоскости S(a // b) и прямой (MK), указать видимость. Определить угол между прямой и плоскостью (рис. 15.25).

28. Найти точки пересечения прямой e с поверхностью тора, указать видимость проекций прямой (рис. 15.26).

29. Построить линию пересечения поверхностей: а) рис. 15.27; б) рис. 15.28.

30. На прямой линии (CD) найти точку, равноудаленную от концов отрезка AB, если A(70; 30; 10), B(35; 15; 40), C(90; 20; 35), D(40; 30; 45).

31. Построить проекцию А₂В₂ отрезка АВ, если его натуральная величина равна 70 мм и А(80; 30; 30), В(30; 60; …).

32. Построить равносторонний треугольник АВС, если задана его сторона АВ и известно, что плоскость треугольника составляет 45° с плоскостью проекций П₂, А(125; 30; 20), В(80; 30; 40). Определить число решений.

33. Построить: а) изометрию цилиндра и винтовой линии (задача 9, рис. 15.9); б) диметрию конуса и линии e (задача 12, рис. 15.12).

34. Построить развертку: а) поверхности призмы (рис. 15.14); б) цилиндрической поверхности и винтовой линии (задача 9, рис. 15.9); в) конической поверхности и линии e (задача 12, рис. 15.12); г) сферы радиуса 50 мм.