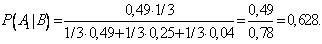Теорема умножения вероятностей. Формула полной вероятности. Формула Байеса

Вероятность произведения двух событий (совместного появления этих событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило:

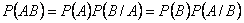
Следствие 1. Обобщим теорему на случай трех событий:

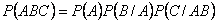
Следствие 2. Обобщим теорему на случай 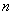событий: в случае произведения нескольких зависимых событий вероятность равна произведению одного из них на условные вероятности всех остальных при условии, что вероятность каждого последующего вычисляется в предположении, что все остальные события уже совершились:

.

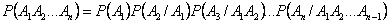Если событие А может произойти только при выполнении одного из событий

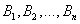, которые образуют полную группу несовместных событий, то вероятность события Авычисляется по формуле

.

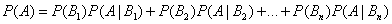Эта формула называется формулой полной вероятности.

Вновь рассмотрим полную группу несовместных событий 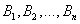, вероятности появления которых 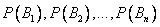. Событие А может произойти только вместе с каким-либо из событий 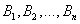, которые будем называть гипотезами. Тогда по формуле полной вероятности

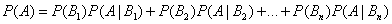
Если событие А произошло, то это может изменить вероятности гипотез .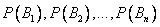

По теореме умножения вероятностей

,

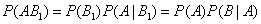откуда

.

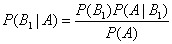Аналогично, для остальных гипотез

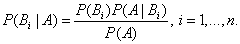
Полученная формула называется формулой Байеса (формулой Бейеса). Вероятности гипотез 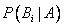называются апостериорными вероятностями, тогда как 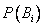- априорными вероятностями.

1. В магазин поступила новая продукция с трех предприятий. Процентный состав этой продукции следующий: 20% - продукция первого предприятия, 30% - продукция второго предприятия, 50% - продукция третьего предприятия; далее, 10% продукции первого предприятия высшего сорта, на втором предприятии - 5% и на третьем - 20% продукции высшего сорта. Найти вероятность того, что случайно купленная новая продукция окажется высшего сорта.

Решение. Обозначим через В событие, заключающееся в том, что будет куплена продукция высшего сорта, через 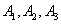обозначим события, заключающиеся в покупке продукции, принадлежащей соответственно первому, второму и третьему предприятиям.

Можно применить формулу полной вероятности, причем в наших обозначениях:

Подставляя эти значения в формулу полной вероятности, получим искомую вероятность:

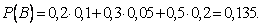
2. Один из трех стрелков вызывается на линию огня и производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго - 0,5; для третьего - 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.

Решение. Возможны три гипотезы:

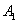- на линию огня вызван первый стрелок,

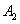- на линию огня вызван второй стрелок,

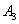- на линию огня вызван третий стрелок.

Так как вызов на линию огня любого стрелка равновозможен, то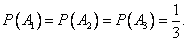

В результате опыта наблюдалось событие В - после произведенных выстрелов мишень не поражена. Условные вероятности этого события при сделанных гипотезах равны:

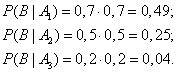
по формуле Байеса находим вероятность гипотезы 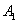после опыта: