Особые решения. Нарушение единственности. Примеры.

Особые решения:

Решение 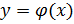дифф. ур – ия 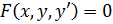называется особым, если в каждой точке нарушается свойство единственности, т.е. если через каждую его точку 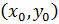кроме этого решения проходит и другое решение, имеющее в точке 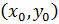ту же касательную, что и решение 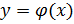, но не совпадающее с ним в сколь угодно малой окрестности 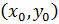. График особого решения называем особой интегральной кривой ур – ия .

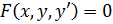Иначе:

Функция 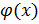называется особым решением дифференциального уравнения 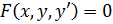, если единственность решения нарушается в каждой точке этой функции в области определения дифференциального уравнения. Геометрически это означает, что через каждую соответствующую точку 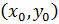проходит более одной интегральной кривой с общей касательной.

// На экзамене можно написать любое из двух определений (какое лучше запоминается).

Особое решение дифференциального уравнения не описывается общим интегралом. Поэтому, оно не выводится из общего решения ни при каком значении постоянной C.

Нарушение единственности:

Если ПДК (p – дискриминантная кривая) распадается на несколько ветвей, то нужно установить, является ли каждая в отдельности ветвь решением ур – ия 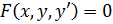, и если является, то будет ли оно особым решением, т.е. нарушается ли единственность в каждой его точке.

Примеры: 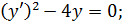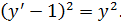//На экзамене решить самому, хотя бы в общем виде. Можно другие примеры, подходящие по определению.

13. Способы определения особых решений. p иC – дискриминантные кривые.

Особые решения Df.

Функция 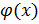называется особым решением дифференциального уравнения 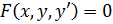, если единственность решения нарушается в каждой точке этой функции в области определения дифференциального уравнения. Геометрически это означает, что через каждую соответствующую точку 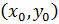проходит более одной интегральной кривой с общей касательной.

Способ 1: Исследование p -дискриминанта дифференциального уравнения. Если функция 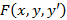и ее частные производные 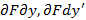непрерывны в области определения дифференциального уравнения, то особое решение находится из системы уравнений:

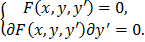
Cпособ 2 нахождения особого решения в виде огибающей семейства интегральных кривых основан на использовании C -дискриминанта.

Пусть 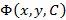является общим решением дифференциального уравнения 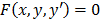. Графически уравнение 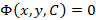соответствует семейству интегральных кривых на плоскости 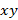. Если функция 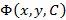и ее частные производные непрерывны, то огибающая семейства интегральных кривых общего решения определяется системой уравнений:

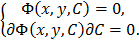
Более общий способ нахождения особых точек дифференциального уравнения основан на одновременном использовании p -дискриминанта и C -дискриминанта.

// В отправленных вам вопросах была опечатка «D и C дискриминантные кривые»

14. ОДУ n-ого порядка. Основные понятия. Приведение ОДУ n-ого порядка, разрешённого относительно производной к системе из n ДУ 1-ого порядка.

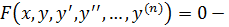ДУ n – ого порядка имеет такой вид, если разрешено относительно 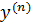, где .

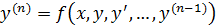Задача Коши – задача нахождения решения 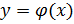ДУ n – ого порядка, удовлетворяющего н.у. (здесь и далее н.у. – начальные условия):

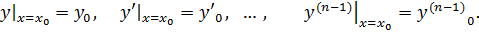
Т.о. для уравнения второго порядка 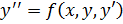начальные условия имеют вид .

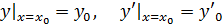Общее решение ДУ n – ого порядка – множество всех его решений, определяемое формулой 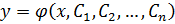, содержащей n произвольных постоянных 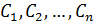таких, что если заданы н.у., то найдутся такие значения 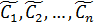, что 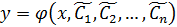будет являться решением уравнения, удовлетворяющим этим н.у.

Частное решение ДУ n – ого порядка – любое решение, получаемое из общего решения при конкретных значениях произвольных постоянных .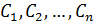

Общий интеграл ур – ия – ур – ие вида 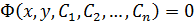, которое определяет неявно общее решение ДУ.

Частный интеграл ДУ получим, дав постоянным 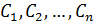конкретные числовые значения.

__

Пусть дано ур – ие 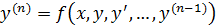. Сопоставим этому ур – ию эквивалентную систему 1 – ого порядка, обозначив

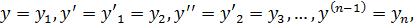
после чего будем иметь систему ур – ий

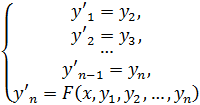, эквивалентную ур – ию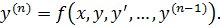

15. Теорема существования единственности Коши для ОДУn-го порядка. ОДУ n-ого порядка, разрешённое относительно производной.

Если в ур – ии 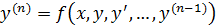ф – ия :
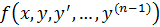а) непрерывна по всем своим аргументам в некоторой области D их изменения,

б) имеет ограниченные в области D частные производные 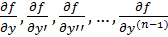по аргументам 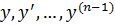, то найдется интервал

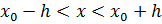, на котором существует единственное решение 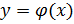ур – ия 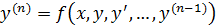, удовлетворяющее условиям

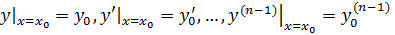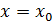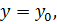
, где значения , , 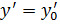…, 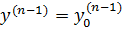содержатся в области D.

___

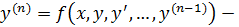ур – ие, разрешенное относительно старшей производной.

16. ДУ высших порядков, допускающие понижение порядка: уравнения, не содержащие искомой функции; уравнения, не содержащие независимой переменной.

Виды ДУ, допускающих понижение порядка:

1. Ур – ие вида 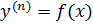. Общее решение находится путем n – кратного интегрирования.

2. Ур – ие не содержащее искомой ф – ии и ее производных до порядка 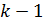включительно: 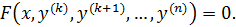Порядок такого ур – ия понижается на k единиц заменой .

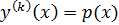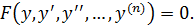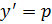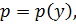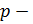3. Ур – ие не содержащее независимого переменного: Подстановка позволяет понизить порядок ур – ия на единицу. (При этом т.е. новая неизвестная ф – ия от )

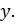4. Ур – ие , однородное относительно аргументов 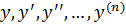, т.е. 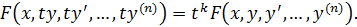Порядок такого ур – ия может быть понижен подстановкой 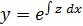, где 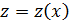, т.е. 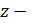новая неизвестная ф – ия от .

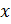5. Ур – ие, записывающееся в дифференциалах, 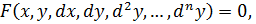в котором ф – ия 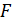однородна относительно своих аргументов 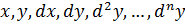, если считать 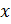и 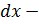первого измерения, а 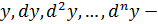измерения .

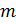17. Линейные ДУ порядкаn. Уравнение Эйлера.

Линейное ДУ n -го порядка – ур – ие вида 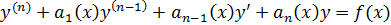, где 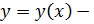неизвестная ф – ия, 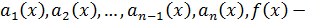известные ф – ии, которые полагаем непрерывными на промежутке .

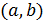Выражение в левой части уравнения называется линейным дифференциальным оператором n -го порядка:

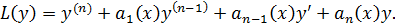
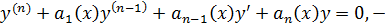однородное линейное ДУ 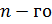порядка.

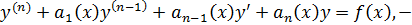неоднородное линейное ДУ 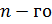порядка.

Уравнением Эйлера называется однородное дифференциальное уравнение вида

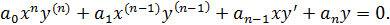
Коэффициенты 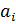— постоянные действительные числа.

Если функция 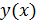— решение уравнения Эйлера, то функция 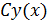тоже является решением уравнения.

Уравнение Эйлера заменой 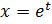сводится к однородному линейному уравнению с постоянными коэффициентами.