Вычисление определенных интегралов

Дана функция y=f(x).

Найти интеграл этой функции на участке [a,b], то есть найти

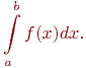
Основу алгоритма численных методов интегрирования составляет геометрический смысл определенного интеграла. Интеграл численно равен площади S криволинейной трапеции, расположенной под подынтегральной кривой f(x) на участке [a,b] (рис.).

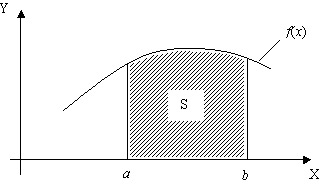
Рис. Геометрический смысл определенного интеграла

Суть всех численных методов интегрирования состоит в приближенном вычислении указанной площади. Поэтому все численные методы являются приближенными.

При вычислении интеграла подынтегральная функция f(x) аппроксимируется интерполяционным многочленом. На практике чтобы не иметь дело с многочленамивысоких степеней, весь участок [a,b] делят на части и интерполяционные многочлены строят для каждой части деления.

Порядок вычисления интеграла численными методами следующий (рис.12.2):

1. Весь участок [a,b] делим на n равных частей с шагом h=(b-a)/n.

2. В каждой части деления подынтегральную функцию f(x) аппроксимируем интерполяционным многочленом. Степень многочлена n = 0,1,2:

3. Для каждой части деления определяем площадь частичной криволинейной трапеции.

4. Суммируем эти площади. Приближенное значение интеграла I равно сумме площадей частичных трапеций

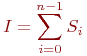
Если в каждой из частей деления интервала [a,b] подынтегральная функция аппроксимируется многочленомнулевой степени, то есть прямой, параллельной оси OX, то метод называется методом прямоугольников.

Если в каждой из частей деления интервала [a,b] подынтегральная функция аппроксимируется многочленом первой степени, то есть прямой, соединяющей две соседние узловые точки, то метод называется методом трапеций.

Если в каждой из частей деления интервала [a,b] подынтегральная функция аппроксимируется многочленомвторой степени, то метод называется методом Симпсона.

Метод прямоугольников

Словесный алгоритм метода прямоугольников:

Если высота каждого частичного прямоугольника равна значению подынтегральной функции в левых концах каждого шага, то метод называется методом левых прямоугольников (рис.). Тогда квадратурная формула имеет вид

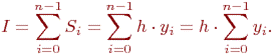
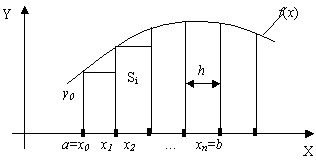
Рис. Метод левых прямоугольников

Если высота каждого частичного прямоугольника равна значению подынтегральной функции в правых концах каждого шага, то метод называется методом правых прямоугольников (рис.). Тогда квадратурная формула имеет вид

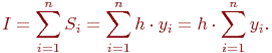
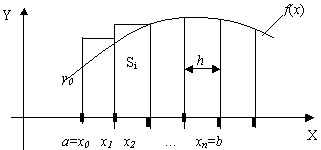
Рис. Метод правых прямоугольников

Точность каждого метода прямоугольников имеет порядок h.

Алгоритм вычисления интеграла построим в виде итерационного процесса поиска с автоматическим выбором шага. На каждом шаге будем уменьшать шаг в два раза, то есть увеличивать число шагов n в два раза. Выход из процесса поиска организуем по точности вычисления интеграла. Начальное число шагов n=2.

Метод трапеций

Приближенное значение интеграла равно сумме площадей частичных трапеций, т.е.

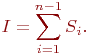
Найдем площади S_i частичных трапеций:

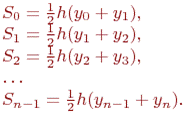
Приближенное значение интеграла равно

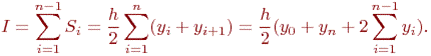
Точность метода трапецийимеет порядок h².

Метод Симпсона

В методе Симпсона в каждой части деления подынтегральная функция аппроксимируется квадратичной параболой a₀x²+a₁x+a₂. В результате вся кривая подынтегральной функции на участке [a,b] заменяется кусочно-непрерывной линией, состоящей из отрезков квадратичных парабол. Приближенное значение интеграла I равно сумме площадей под квадратичными параболами.

Так как для построения квадратичной параболынеобходимо иметь три точки, то каждая часть деления в методе Симпсона включает два шага, L_k=2h.

В результате количество частей деления N2=n/2. Тогда n в методе Симпсона всегда четное число.

Определим площадь S₁ на участке [x₀, x₂](рис.12.2).

Исходя из геометрического смысла определенного интеграла, площадь S₁ равна определенному интегралу от квадратичной параболына участке [x₀, x₂]:

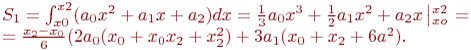
Неизвестные коэффициенты квадратичной параболыа₀ , а₁, а₂ определяем из условия прохождения параболойчерез три узловых точки с координатами (x₀y₀), (x₁y₁), (x₂y₂).

На основании этого условия строим систему линейных уравнений:

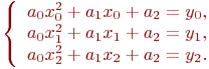
Решая эту систему, найдем коэффициенты параболы.

В результате имеем: ..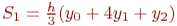

Для участка [x₂, x₄]: ..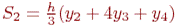

:::::::::::::::::::

Для участка [x_i-1, x_i+1]: .,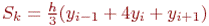

где .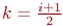

Суммируя все площади S₁ под квадратичными параболами, получим квадратурную формулу по методу Симпсона:

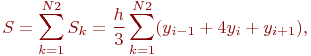
где

N2 - количество частей деления.

Точность метода Симпсонаимеет порядок (h³/h⁴).