Обобщенная постановка смешанной краевой задачи для уравнения параболического типа

Рассмотрим краевую задачу для нестационарного уравнения теплопроводности

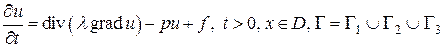(2.16)

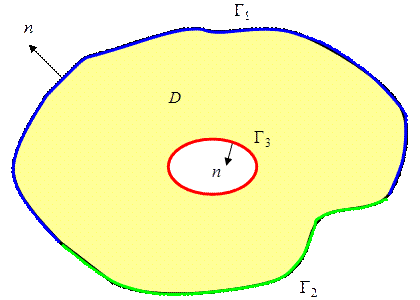
Зададим начальное условие 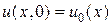и различные граничные условия на разных участках границы:

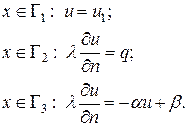(2.17)

Обозначим через 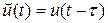функцию на нижнем временном слое ( 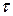‑ шаг сетки по 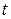) и запишем полудискретизованную по времени неявную схему для уравнения (2.16). Домножим её на пробную функцию 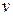и проинтегрируем по области 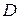. Будем иметь

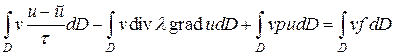
Применяя формулу Гаусса-Остроградского и учитывая при этом граничные условия (2.17), получим

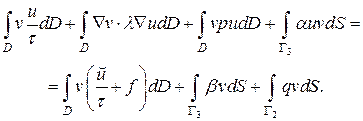(2.18)

Это уравнение должно быть дополнено граничным условием Дирихле (2.17). Призаписи (2.18) учтено, что пробная функция 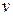равна нулю на участке 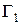границы .

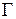В дальнейшем для простоты будем считать, что коэффициенты 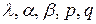постоянны. Кроме того, удобно доопределить параметры 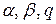нулём на той части границы 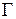, где они не заданы. Тогда интегральное тождество (2.18) можно записать чуть более компактно:

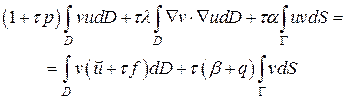(2.19)

Замечание 1. Правая часть 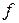исходного уравнения может содержать как распределенные, так и сосредоточенные источники тепла, например

,

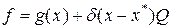где 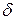‑ дельта-функция Дирака. В этом случае первый интеграл в правой части (2.19) будет равен

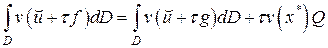. (2.20)

Замечание 2. Интегральное тождество (2.19) не учитывает граничного условия Дирихле на 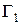; оно должно учитываться отдельно. Для этого существуют несколько приёмов, основанных на модификации матрицы и правой части системы сеточных (алгебраических) уравнений, которые будут построены на основе интегрального тождества (2.19). Однако можно указать способ приближенного учета условий Дирихле уже на стадии записи интегрального тождества. Он состоит в том, чтобы вместо первого из граничных условий (2.17) записать граничное условие 3-го рода в виде

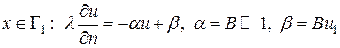
Очевидно, что если разделить это равентство на очень большое число 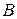, то получим следующее приближение:

.

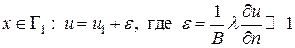При этом структура интегрального тождества (2.19) не меняется, следует лишь должным образом задать коэффициенты 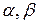на разных участках границы.

Лекция 3. Система уравнений МКЭ

Сетка МКЭ

Покроем область 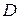сеткой конечных элементов 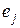, , 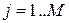так чтобы .

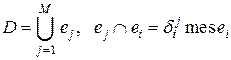Тогда 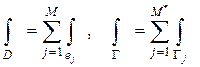. Звёздочка означает, что при интегрировании по границе в сумму входят лишь те конечные элементы 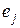, границы которых 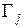хотя частично лежат на границе области .

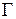Рассмотрим отдельный конечный элемент. Например это многоугольник. Пусть он имеет 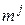узлов. Тогда можно ввести базисные функции этого элемента 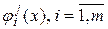. Эти функции линейно независимы и нормированы так, что 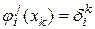. Произвольная функция 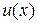на элементе 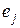может быть представлена разложением по базису

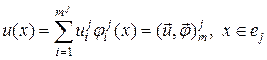(3.1)

Индекс 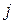обозначает принадлежность к 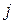-му элементу. В дальнейшем, если это не приводит к недоразумениям, индекс 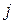часто будем опускать. Индекс 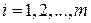используется для локальной нумерации узлов конечного элемента. Следует отметить, что локальные узлы элемента могут совпадать с вершинами многоуголника 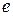, а могут и не совпадать с ними, как показано на рис. 3.1. Наряду с локальной вводят сквозную глобальную нумерацию узлов. Соответствие локальных и глобальных номеров, их координаты, а также связность (т.е. указание, какие узлы образуют элемент) задаётся с помощью двух основных таблиц, которые представляют МКЭ-сетку.

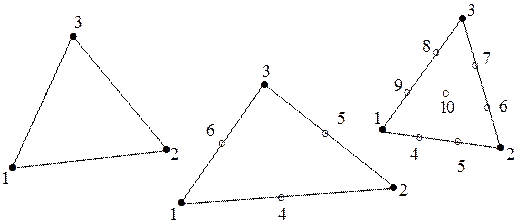
Рис. 3.1. Трехузловой, шестиузловой и десятиузловой
треугольные конечные элементы

Таблица 1. Узлы

№	x	y	b	z
i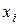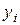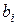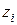
N

Поле 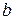(bound) используется, чтобы отличить внутренние узлы ( 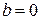) от граничных ( 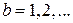). Признак 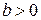позволяет в программе, использующей эту сетку, задавать нужное граничное условие; например, если 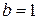, ‑ то это условие Дирихле, если 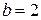, ‑ то ставится условие Неймана, и т.д. на разных участках границы 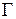. Поле 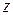(zone) используется, чтобы задавать различные функции для коэффициентов решаемой задачи; например коэффициент теплопроводности в композитных материалах: 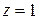‑ сталь, 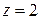‑ аллюминий и т.д.

Таблица 1 не позволяет нарисовать МКЭ-сетку, а только узлы. Это значит, что требуется еще одна таблица элементов, или таблица связности, в которой указывались бы связи узлов ребрами и то, какие узлы образуют элемент.

Таблица 2. Элементы

№	n1	n2	n3	…	nm	z
j
M

Строка 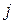таблицы элементов показывает, что конечный элемент 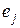‑ это треугольник с вершинами в узлах 213, 45 и 41246 и расположенный в зоне 3. Таким образом, эта таблица указывает соответствие локальных и глобальных номеров узлов. При этом локальный порядок нумерации определен заранее, например как показано на рис. 3.1. Принято, чтобы «основные» узлы элемента, т.е. узлы, совпадающие с вершинами многоугольника, нумеровались против хода часовой стрелки.

С томощью двух таблиц – узлов и элементов – легко нарисовать МКЭ-сетку. Для этого в цикле 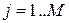рисуем каждый элемент. Конечный элемент 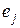рисуется так: в строке 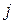таблицы 2 последовательно берутся глобальные номера 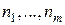, для каждого из них в строках 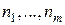таблицы 1 берутся координаты и узлы соединяются ребрами в порядке 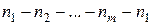. Таким образом, таблицы узлов и элементов однозначно определяют МКЭ-сетку. На практике наряду с этими таблицами удобно пользоваться таблицами инцидентности (или таблицами соседей). Так, для фрагмента сетки, показанной на рис. 3.2 таблицы 3, 4 инцидентых узлов и элементов выглядят так (заполнены только 1-я и 19-я строки)

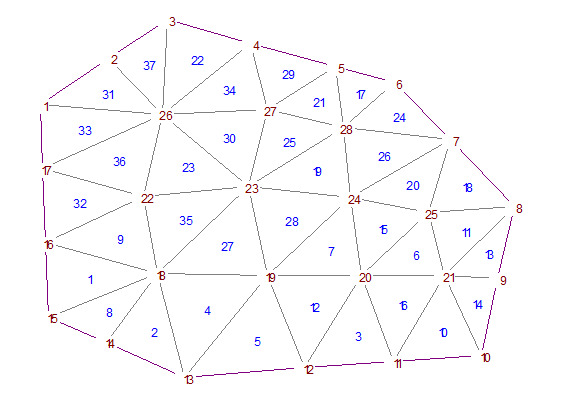
Рис. 3.2. Фрагмент МКЭ-сетки

Таблица 3. Инцидентные узлы

№	e1	e2	e3	e4	e5	e6	…	ep
N

Таблица 4. Инцидентные элементы

№	k1	k2	k3	k4	k5	k6	…	kz
N