Свойства функций непрерывных на отрезке

1.Если функция y = f(x) непрерывна на отрезке [a, b], то она ограничена на этом отрезке (рис. 5.9).

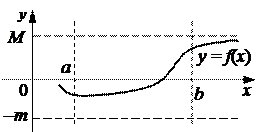Рис. 5.9. Ограниченная функция

2. Если функция y = f(x) непрерывна на отрезке [a, b], то она достигает на этом отрезке своего наибольшего М и наименьшего m значения (теорема Вейерштрасса) (рис. 5.10).

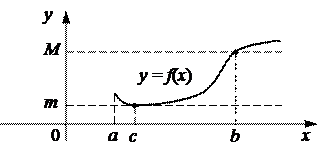Рис. 5.10. Наименьшее и наибольшее значения функция

3. Если функция y = f(x) непрерывна на отрезке [a, b], а ее значения на концах отрезка f(a) и f(b) имеют разные знаки, то найдется точка такая, что f(c) = 0 (теорема Больцано-Коши) (рис. 5.11).

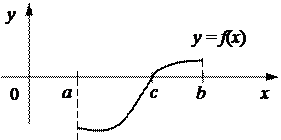Рис. 5.11. К теореме Больцано-Коши

Легко показать, что все эти свойства не имеют силы для функции y = f(x), непрерывной на интервале, а не на отрезке. Например, как показано на рисунке ниже, непрерывная на интервале (a, b) функция y = f(x) не удовлетворяет свойству 1 и свойству 2 в части наибольшего ее значения (рис. 5.12).

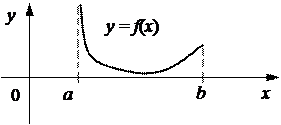Рис. 5.12. Функция, непрерывная только на интервале

Пример 5.1.

Найти область определения функции .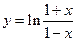

Решение. Выражение, стоящее в правой части равенства, имеет смысл, если аргумент натурального логарифма больше нуля, а знаменатель дроби не равен нулю. То есть

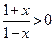и .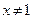

Исследуя левую часть неравенства можно построить интервалы ее положительного и отрицательного значений.

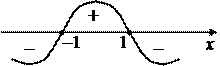Из рисунка видно, что областью решений неравенства является интервал (–1; 1). Следовательно, область определения исходной функции: x 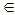(–1; 1).

В примерахустановить четность функций:

Пример 5.2. .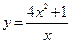

Решение. Найдем y(–x): 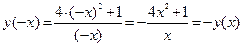. Функция нечетная.

Пример 5.3. .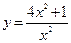

Решение. Найдем y(–x): 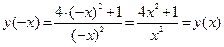. Функция четная.

Пример 5.4. .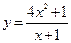

Решение. Найдем y(–x): 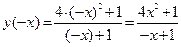. По виду функция y(–x)не равна ни y(x), ни –y(x).Проверим это для какой-либо произвольной точки, например, x = 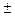2.

; .

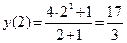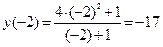Функция не является ни четной, ни нечетной, т. е. это функция общего вида.

Пример 5.5.Найти предел функции .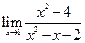

Решение. Используем свойство непрерывности элементарных функций в области их определения. Из свойства следует, что если существует значение функции в той точке, к которой стремится x, то предел функции в этой точке существует и равен значению функции.

Поэтому первым шагом при вычислении предела является подстановка в функцию условия предельного перехода:

.

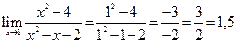Пример 5.6.Найти предел функции .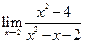

Решение. Подставляем x = 2 в формулу функции. Получаем:

.

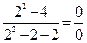В таком случае говорят, что данный предел представляет собой неопределенность вида 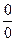, которую надо раскрыть.

Для функций, представляющих собой алгебраическую рациональную дробь, основным методом раскрытия неопределенностей является разложение числителя и знаменателя на множители и сокращение множителей, обращающих в нуль числитель и знаменатель. Такое действие является правомерным, т. к. при определении понятия предела функции специально подчеркивалось, что значение функции в самой точке, к которой стремится x, (равно как и его отсутствие), никак не влияет на предел функции в этой точке.

Поэтому сокращение указанных множителей при определении предела не является сокращением на ноль. Ясно, что числитель заданной функции можно разложить на множители по формуле «разность квадратов», а знаменатель — используя решение соответствующего квадратного уравнения или способом группировки.

Тогда

.

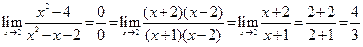Пример 5.7.Найти предел функции

.

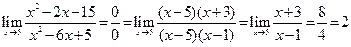Пример 5.8.Найти предел функции

.

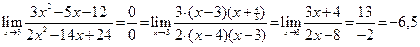Пример 5.9.Найти предел функции .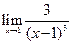

Решение. У заданной функции в числителе постоянная величина не равная нулю, а в знаменателе бесконечно малая функция при 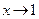. Следовательно, заданная функция является бесконечно большой функцией при 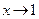и ответ нужно записать так:

.

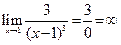Здесь вместо значения ноль понимается бесконечно малая величина. В этом случае обычно говорят, что предел заданной функции бесконечен (или равен бесконечности).

Пример 5.10.Найти предел функции .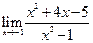

Решение. Подставив x = –1, имеем частное от деления функции, предел которой не равен нулю, на бесконечно малую функцию при 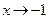. Это значит, что предел заданной функции бесконечен, т. е.

.

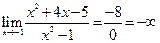Пример 5.11.Найти предел функции .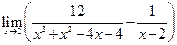

Решение. Подставив x = 2, убеждаемся, что предел каждого из слагаемых заданной алгебраической суммы бесконечен. То есть имеем дело с пределом вида 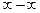. Такой предел является неопределенностью и в зависимости от вида функций-слагаемых может оказаться равным как бесконечности, так и любому конкретному числу, включая ноль. Для раскрытия такой неопределенности следует перейти к неопределенности вида 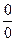путем приведения дробей к общему знаменателю и выполнения сложения или вычитания, а затем действовать аналогично ранее рассмотренным случаям.

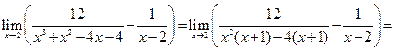
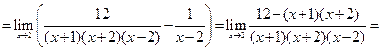
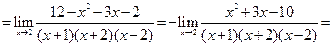
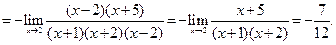
Пример 5.12.Найти предел функции .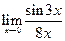

Решение. Чтобынайти заданный предел, нужно домножить числитель и знаменатель на 3, после чего вынести за знак предела множитель 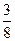и использовать первый замечательный предел. Запишем

.

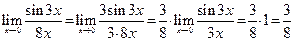Пример 5.13.Найти предел функции

.►

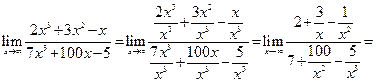
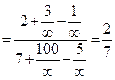Пример 5.14.Найти предел функции , .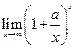

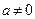Решение. Для нахождения данного предела следует числитель и знаменатель дроби разделить на a,сделать замену переменной 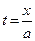, а затем использовать непрерывность степенной функции и второй замечательный предел

.

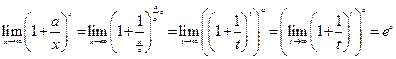Пример 5.15.Найти предел функции

.

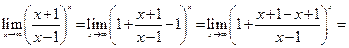
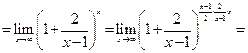
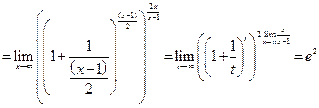Пример 5.16.Найти и классифицировать точки разрыва функции

.

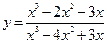Решение. Так как заданная функция является элементарной, то точками разрыва являются только точки, в которых функция не существует, т. е. точки, в которых знаменатель дроби равен нулю.

Поэтому найдем корни знаменателя:

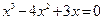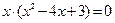; ; x₁= 0; x₂= 1; x₃ = 3.

а) x = 0. Для обоих односторонних пределов выполняется

.

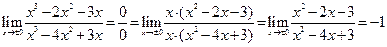Точка устранимого разрыва.

б) x = 1

.

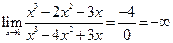Точка разрыва 2-го рода.

в) x = 3. Для обоих односторонних пределов выполняется

.

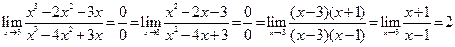Точка устранимого разрыва.

Пример 5.17.

Найти асимптоты графика функции

.

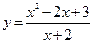Решение.

а)Ищем вертикальные асимптоты. Обычно их определяют точки разрыва или точки на краях интервала области определения функции.

Очевидно, что точка x = –2 точка разрыва 2-го рода с бесконечными односторонними пределами, т. к.

;

.

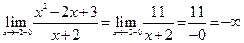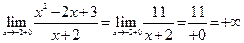Следовательно, прямая x = –2 — вертикальная асимптота графика заданной функции.

б)Ищем горизонтальные асимптоты:

.

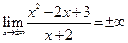Горизонтальных асимптот нет. Ищем наклонные асимптоты.

в)Ищем наклонные асимптоты. Для уравнения прямой y = kx + b вычисляем значения коэффициентов для наклонной асимптоты справа:

;

.

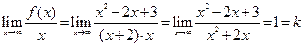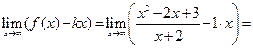
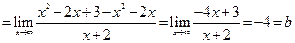Следовательно, прямая y = x – 4 —наклонная асимптота справа заданной функции.

Аналогично можно показать при 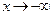, что эта же прямая является наклонной асимптотой слева заданной функции.

Вопросы для самоконтроля

1. Что такое функция одной переменной?

2. Что называется аргументом, областью определения и областью значений функции?

3. Назовите основные способы задания функций.

4. Дайте определения основным свойствам функции: четности и нечетности, монотонности, ограниченности, периодичности.

5. Запишите формулы и изобразите примерные графики основных (простейших) элементарных функций: константы, степенной функции (при различных значениях показателя степени), показательной и логарифмической функций, тригонометрических и обратных тригонометрических функций.

6. Какие функции, кроме простейших, являются элементарными функциями?

7. Дайте определение предела функции в точке и в бесконечности. Как обозначается предел функции?

8. Как определяются и записываются односторонние пределы?

9. Какие функции называются бесконечно малой и бесконечно большой функциями (величинами) в точке и бесконечности?

10. Сформулируйте основные свойства бесконечно малых и бесконечно больших функций.

11. Сформулируйте основные теоремы о пределах суммы, разности, произведения, частного, сложной функции.

12. Запишите два предела, называемых замечательными пределами.

13. Что называется асимптотой графика функции?

14. Назовите виды асимптот и сформулируйте правила их нахождения.

15. Сформулируйте условия непрерывности функции в точке.

16. Какая функция называется непрерывной на отрезке?

17. Что называется точкой разрыва функции? Какие точки являются точками разрыва элементарных функций?

18. Дайте классификацию точек разрыва.

19. Сформулируйте свойства функций непрерывных на отрезке.