Свойства функций, непрерывных на отрезке
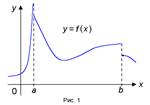
Теорема 1 (об ограниченности непрерывной функции). Если функция f(x) непрерывна на отрезке [a, b], то она ограничена на этом отрезке, т.е. существует такое число C> 0, что "x О [a, b] выполняется неравенство |f(x)| ≤ C.
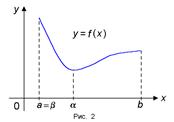
Теорема 2 (Вейерштрасс). Если функция f(x) непрерывна на отрезке [a, b], то она достигает на этом отрезке своего наибольшего значения M и наименьшего значения m, т.е. существуют точки α, β О [a, b] такие, что m = f(α) ≤ f(x) ≤ f(β) = M для всех x О [a, b] (рис.2).
Наибольшее значение M обозначается символом maxx О [a, b] f(x), а наименьшее значение m — символом minx О [a, b] f(x).
 Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует Геометрический смысл производной. Рассмотрим график функции y = f ( x ):
Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует Геометрический смысл производной. Рассмотрим график функции y = f ( x ): 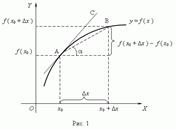 Из рис.1 видно, что для любых двух точек A и B графика функции:
Из рис.1 видно, что для любых двух точек A и B графика функции: 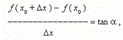 где
где 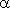 - угол наклона секущей AB. Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точку B, то
- угол наклона секущей AB. Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точку B, то 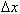 неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоит геометрический смысл производной. Механический смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан: координата x движущейся точки – известная функция x ( t ) времени t. В течение интервала времени от t0 до t0 +
неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоит геометрический смысл производной. Механический смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан: координата x движущейся точки – известная функция x ( t ) времени t. В течение интервала времени от t0 до t0 + 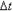 точка перемещается на расстояние: x ( t0 +
точка перемещается на расстояние: x ( t0 + 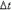 ) - x ( t0 ) =
) - x ( t0 ) = 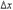 , а её средняя скорость равна: va =
, а её средняя скорость равна: va = 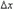 /
/ 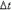 . При
. При 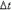
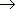 0 значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью v ( t0) материальной точки в момент времени t0 . Но по определению производной мы имеем:
0 значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью v ( t0) материальной точки в момент времени t0 . Но по определению производной мы имеем: 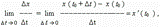 отсюда, v ( t0) = x’ ( t0) , т.e. скорость – это производная координаты по времени. В этом и состоит механический смыслпроизводной. Аналогично, ускорение – это производная скорости по времени: a = v’ ( t ). УРАВНЕНИЯ КАСАТЕЛЬНОЙ И НОРМАЛИ К КРИВОЙ.Рассмотрим кривую, уравнение которой есть y=f(x). Возьмем на этой кривой точку M(x0, y0), и составим уравнение касательной к данной кривой в точке M, предполагая, что эта касательная не параллельна оси Oy. Уравнение прямой с угловым коэффициентом в общем виде есть у=kx + b. Поскольку для касательной k= f'(x0), то получаем уравнение y= f'(x0)·x + b. Параметр b найдем из условия, что касательная проходит через точку M(x0, y0). Поэтому ее координаты должны удовлетворять уравнению касательной: y0= f'(x0)·x0 + b. Отсюда b=y0–f'(x0)·x0. Таким образом, получаем уравнение касательной y= f'(x0)·x +y0 – f'(x0)·x0 или
отсюда, v ( t0) = x’ ( t0) , т.e. скорость – это производная координаты по времени. В этом и состоит механический смыслпроизводной. Аналогично, ускорение – это производная скорости по времени: a = v’ ( t ). УРАВНЕНИЯ КАСАТЕЛЬНОЙ И НОРМАЛИ К КРИВОЙ.Рассмотрим кривую, уравнение которой есть y=f(x). Возьмем на этой кривой точку M(x0, y0), и составим уравнение касательной к данной кривой в точке M, предполагая, что эта касательная не параллельна оси Oy. Уравнение прямой с угловым коэффициентом в общем виде есть у=kx + b. Поскольку для касательной k= f'(x0), то получаем уравнение y= f'(x0)·x + b. Параметр b найдем из условия, что касательная проходит через точку M(x0, y0). Поэтому ее координаты должны удовлетворять уравнению касательной: y0= f'(x0)·x0 + b. Отсюда b=y0–f'(x0)·x0. Таким образом, получаем уравнение касательной y= f'(x0)·x +y0 – f'(x0)·x0 или | y = f '(x0)·(x – x0) + f(x0) |
Если касательная, проходящая через точку М(x0,y0) параллельна оси ординат (т.е. производная в этой точке не существует), то ее уравнение x= x0.
Наряду с касательной к кривой в данной точке часто приходится рассматривать нормаль.
Нормалью к кривой в данной точке называется прямая, проходящая через эту точку перпендикулярно к касательной в  данной точке.
данной точке.
Из определения нормали следует, что ее угловой коэффициент kn связан с угловым коэффициентом касательной k равенством:
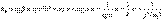 .
.
Учитывая, что нормаль также как и касательная проходит через точку M(x0,y0), то уравнение нормали к кривой y= f(x) в данной точке M имеет вид:
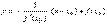
Ясно, что если касательная параллельна оси Ox, т.е.f'(x0) = 0 и ее уравнение имеет вид y= y0, то нормаль в этой же точке будет перпендикулярна оси Ox. Значит, ее уравнение имеет вид x= x0.
21 22 23
1. y= sin x. Вновь воспользуемся определением производной.
Так как, f(x+Δx)=sin(x+Δx), то
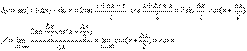
Таким образом,
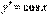
Аналогично можно показать, что
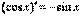


Наши рекомендации
