По выполнению контрольной работы №1 4 страница
Пример 1. Найти интеграл 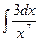 .
.
Решение: Воспользуемся определением степени с отрицательным показателем 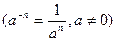 и найдем неопределенный интеграл от степени:
и найдем неопределенный интеграл от степени:
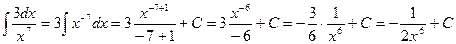 .
.
Пример 2. Найти интеграл 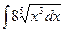 .
.
Решение: Воспользуемся определением степени с дробным показателем 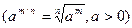 и найдем неопределенный интеграл от степени:
и найдем неопределенный интеграл от степени:
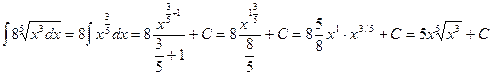 .
.
Пример 3. Найти интеграл 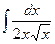 .
.
Решение: Воспользуемся определением степени с дробным и отрицательным показателем и правилом умножения степеней с одинаковыми основаниями 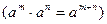 и найдем неопределенный интеграл от степени:
и найдем неопределенный интеграл от степени:
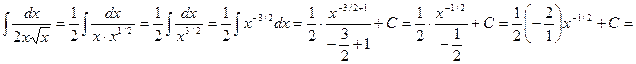
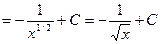 .
.
Пример 4. Найти интеграл 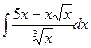 .
.
Решение: Воспользуемся определением степени с дробным показателем 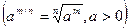 , правилами действия над степенями с одинаковыми основаниями
, правилами действия над степенями с одинаковыми основаниями 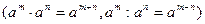 , правилом деления суммы на число и найдем интеграл от каждого слагаемого отдельно. Имеет:
, правилом деления суммы на число и найдем интеграл от каждого слагаемого отдельно. Имеет:
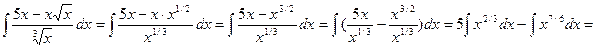
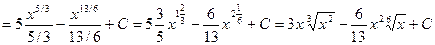 .
.
Заметим, что произвольные постоянные, входящие по определению в каждый из слагаемых неопределенных интегралов, объединяются в одну произвольную постоянную.
Пример 5. Найти интеграл 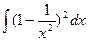 .
.
Решение: Раскроем скобки по формуле 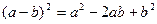 и неопределенный интеграл от полученной алгебраической суммы функции заменим такой же алгебраической суммой неопределенных интегралов от каждой функции:
и неопределенный интеграл от полученной алгебраической суммы функции заменим такой же алгебраической суммой неопределенных интегралов от каждой функции:
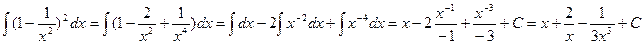
Пример 6. Найти интеграл 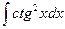 .
.
Решение: Для нахождения интеграла воспользуемся формулой 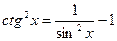 и свойствами неопределенного интеграла:
и свойствами неопределенного интеграла:
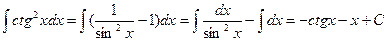 .
.
Интегрирование методом подстановки. Если интеграл затруднительно привести к табличному с помощью элементарных преобразований, то в этом случае пользуются методом подстановки.
Сущность этого метода заключается в том, что путем введения новой переменной удается свести данный интеграл к новому интегралу, который сравнительно легко берется непосредственно.
Для интегрирования методом подстановки можно использовать следующую схему:
- часть подынтегральной функции надо заменить новой переменной;
- найти дифференциал от обеих частей замены;
3. все подынтегральное выражение выразить через новую переменную (после чего должен получится табличный интеграл);
4. найти полученный табличный интеграл;
5. сделать обратную замену.
Пример 7. Найти интеграл 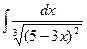 .
.
Решение: Произведем подстановку 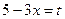 , тогда
, тогда 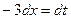 , откуда
, откуда 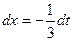 . Далее получаем:
. Далее получаем:
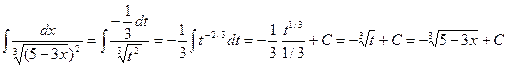 .
.
Пример 8. Найти интеграл 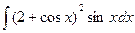 .
.
Решение: Сначала положим 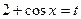 , тогда
, тогда 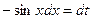 , откуда
, откуда 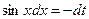 . Далее получаем:
. Далее получаем:
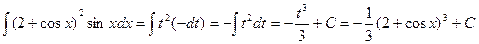 .
.
Пример 9. Найти интеграл 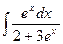 .
.
Решение: Положим 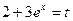 , тогда
, тогда 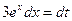 , откуда
, откуда 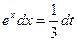 . Далее получаем:
. Далее получаем:
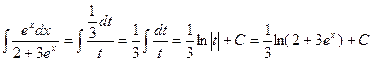 .
.
Пример 10. Найти интеграл 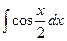 .
.
Решение: Положим 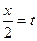 , тогда
, тогда 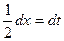 , откуда
, откуда 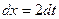 . Далее получаем:
. Далее получаем:
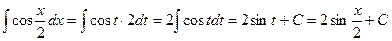 .
.
В практике интегрирования часто встречаются интегралы, для нахождения которых можно использовать следующие формулы ( 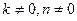 – постоянные):
– постоянные):
1. 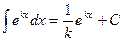 . 2. . 2. 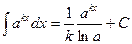 . 3. . 3. 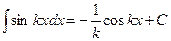 . 4. . 4. 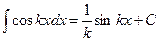 . . | 5. 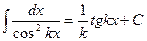 . 6. . 6. 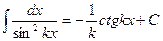 . 7. . 7. 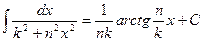 . 8. . 8. 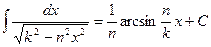 |
Так, при нахождении 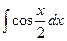 можно использовать формулу
можно использовать формулу 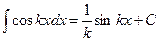 , где
, где 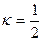 . Тогда
. Тогда 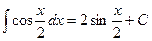 .
.
Определенный интеграл.
Пусть функция 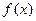 определена на отрезке
определена на отрезке 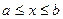 . Допустим для простоты, что функция
. Допустим для простоты, что функция 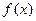 в указанном промежутке неотрицательна и
в указанном промежутке неотрицательна и 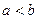 . Разобьем этот отрезок на n частей точками
. Разобьем этот отрезок на n частей точками 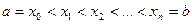 . На каждом из частичных отрезков
. На каждом из частичных отрезков 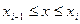
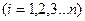 возьмем произвольную точку сi и составим сумму:
возьмем произвольную точку сi и составим сумму:
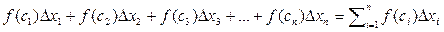 ,
,
где 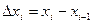 . Эта сумма носит название интегральной суммы функции
. Эта сумма носит название интегральной суммы функции 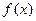 на отрезке
на отрезке 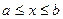 .
.
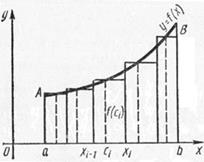 Рис. 15 Рис. 15 | Геометрически (рис. 15) каждое слагаемое интегральной суммы равно площади прямоугольника с основанием 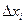 и высотой и высотой 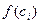 , а вся сумма равна площади «ступенчатой фигуры», получающейся объединением всех указанных выше прямоугольников. Очевидно, что при всевозможных разбиениях отрезка , а вся сумма равна площади «ступенчатой фигуры», получающейся объединением всех указанных выше прямоугольников. Очевидно, что при всевозможных разбиениях отрезка 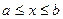 на части получим различные интегральные суммы, а следовательно, и различные «ступенчатые фигуры». на части получим различные интегральные суммы, а следовательно, и различные «ступенчатые фигуры». |
Будем увеличивать число точек разбиения так, чтобы длина наибольшего из отрезков 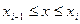 стремилась к нулю. Во многих случаях при таком разбиении интегральная сумма будет стремиться к некоторому конечному пределу, не зависящему ни от способа, каким выбираются точки деления
стремилась к нулю. Во многих случаях при таком разбиении интегральная сумма будет стремиться к некоторому конечному пределу, не зависящему ни от способа, каким выбираются точки деления 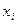 , ни от того, как выбираются промежуточные точки
, ни от того, как выбираются промежуточные точки 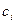 .
.
Этот предел и называется определенным интегралом от функции 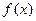 на отрезке
на отрезке 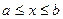 .
.
Определенным интегралом от функции 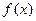 на отрезке
на отрезке 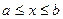 называется предел, к которому стремится интегральная сумма при стремлении к нулю длины наибольшего частичного интервала. Он обозначается символом
называется предел, к которому стремится интегральная сумма при стремлении к нулю длины наибольшего частичного интервала. Он обозначается символом 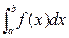 и читается «интеграл от a до b от функции
и читается «интеграл от a до b от функции 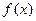 по dx» или, короче, «интеграл от a до b от
по dx» или, короче, «интеграл от a до b от 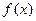 dx».
dx».
По определению,
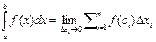 .
.
Число а называется нижним пределом интегрирования, число b – верхним; отрезок 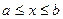 – отрезком интегрирования.
– отрезком интегрирования.
Заметим, что всякая непрерывная на отрезке 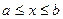 функция
функция 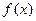 интегрируема на этом отрезке.
интегрируема на этом отрезке.
Если интегрируемая на отрезке 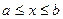 функция
функция 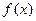 неотрицательна, то определенный интеграл
неотрицательна, то определенный интеграл 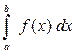 численно равен площади S криволинейной трапеции аABb, ограниченной графиком функции
численно равен площади S криволинейной трапеции аABb, ограниченной графиком функции 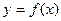 , осью абсцисс и прямыми
, осью абсцисс и прямыми 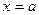 и
и 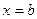 (рис. 15), т.е.
(рис. 15), т.е. 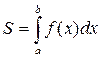 . В этом и заключается геометрический смысл определенного интеграла.
. В этом и заключается геометрический смысл определенного интеграла.
Основные свойства определенного интеграла. Все свойства сформулированы в предположении, что рассматриваемые функции интегрируемы в соответствующих промежутках.
1. Определенный интеграл с одинаковыми пределами равен нулю:
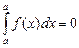 .
.
2. При перестановке пределов интегрирования знак интеграла меняется на противоположный:
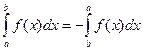 .
.
3. Отрезок интегрирования можно разбивать на части:
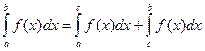 , где
, где 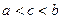 .
.
4. Постоянный множитель можно выносить за знак интеграла:
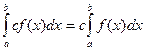 .
.
5. Интеграл от алгебраической суммы функций равен той же алгебраической сумме интегралов от всех слагаемых:
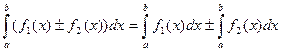 .
.
Непосредственное вычисление определенного интеграла. Для вычисления определенного интеграла, когда можно найти соответствующий неопределенный интеграл, служат формулой Ньютона – Лейбница
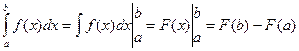 ,
,
т.е. определенный интеграл равен разности значений любой первообразной функции при верхнем и нижнем пределах интегрирования.
Пример 1. Вычислить интеграл 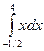 .
.
Решение: Применив указанное правило, вычислим данный определенный интеграл:
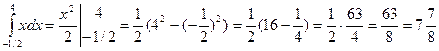 .
.
Пример 2. Вычислить интеграл 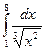 .
.
Решение: Воспользуемся определением степени с дробным и отрицательным показателем и вычислим определенный интеграл:
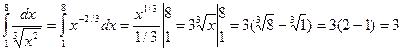 .
.
Пример 3. Вычислить интеграл 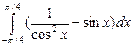 .
.
Решение: Интеграл от разности функции заменим разностью интегралов от каждой функции:
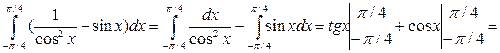
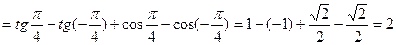 .
.
Пример 4. Вычислить интеграл 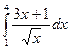 .
.
Решение: Воспользуемся определением степени с дробным показателем, правилом деления суммы на число и вычислим определенный интеграл от каждого слагаемого отдельно:
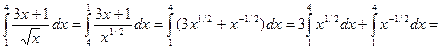
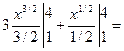
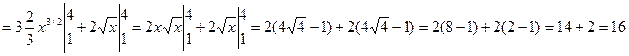 .
.
Приложение определенного интеграла. Понятие определенного интеграла широко применяется для вычисления различных геометрических и физических величин.
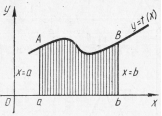 Рис. 16 Рис. 16 | 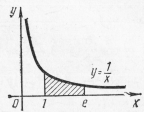 Рис. 17 Рис. 17 |
Площади плоских фигур. Площадь криволинейной трапеции aABb (рис. 16), ограниченной графиком непрерывных функций 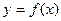 (где
(где 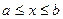 ), отрезком ab оси Ох и отрезками прямых
), отрезком ab оси Ох и отрезками прямых 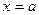 и
и 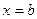 , вычисляется по формуле:
, вычисляется по формуле:
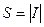 , где , где 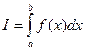 | (1) |
Пример 10. Вычислить площадь фигуры, ограниченной гиперболой 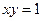 , осью Ох и прямыми
, осью Ох и прямыми 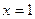 и
и 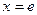 (рис. 17).
(рис. 17).
Решение: Применяя формулу (1), получаем:
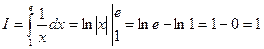 ,
, 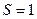 кв. ед.
кв. ед.
Пример 11. Вычислить площадь фигуры, ограниченной параболой 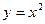 , прямыми
, прямыми 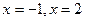 и осью абсцисс (рис. 18).
и осью абсцисс (рис. 18).
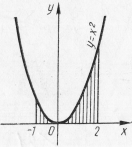 Рис. 18 Рис. 18 | 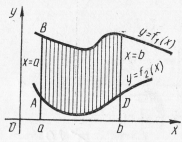 Рис. 19 Рис. 19 |
Решение: Применяя формулу (1), получаем:
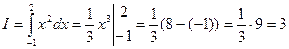 ;
; 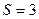 кв. ед.
кв. ед.
Площадь фигуры ABCD (рис. 19), ограниченной графиками непрерывных функций 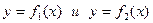 , (где
, (где 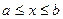 ) и отрезками прямых
) и отрезками прямых 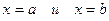 , вычисляется по формуле:
, вычисляется по формуле:
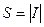 , где , где 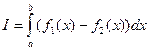 | (2) |
Пример 12. Вычислить площадь фигуры, ограниченной кривой 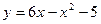 и осью Ох (рис. 20).
и осью Ох (рис. 20).
Решение: Найдем пределы интегрирования, т.е. абсциссы точек пересечения графиков функций 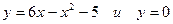 (ось Ох). Для этого решим систему
(ось Ох). Для этого решим систему
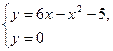 .
.
Имеем 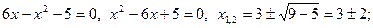
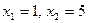 .
.
Теперь найдем искомую площадь по формуле (2): 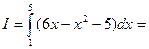
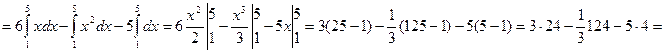
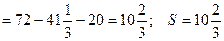 кв.ед.
кв.ед.
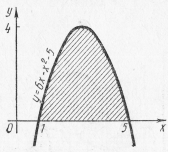 Рис. 20 Рис. 20 | 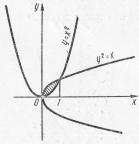 Рис. 21 Рис. 21 |
Пример 13. Вычислить площадь фигуры, ограниченной линиями 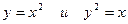
(рис. 21).
Решение: Найдем пределы интегрирования, т.е. абсциссы точек пересечения графиков функций 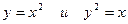 . Для этого решим систему
. Для этого решим систему
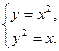
Имеем: 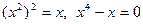 ,
, 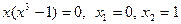 . Искомую площадь вычисляем по формуле (2), при
. Искомую площадь вычисляем по формуле (2), при 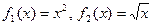 :
:
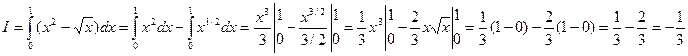
 кв. ед.
кв. ед.
Пример 14. Вычислить площадь фигуры, ограниченной параболами 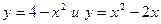 (рис. 22).
(рис. 22).
Решение: Найдем пределы интегрирования, т.е. абсциссы точек пересечения графиков функций 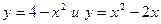 . Для этого решим систему:
. Для этого решим систему:
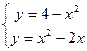 .
.
Имеем: 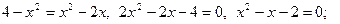
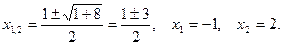
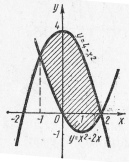 Рис. 22 Рис. 22 | 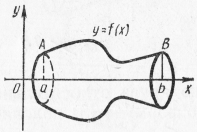 Рис. 23 Рис. 23 |
Искомую площадь вычисляем по формуле (2):
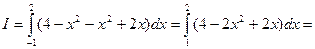
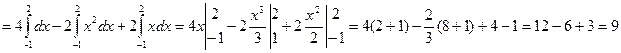 .
.
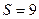 кв. ед.
кв. ед.
Объем тела вращения. Объем тела, образованного вращением вокруг оси Ох криволинейной трапеции aABb, ограниченной непрерывной кривой 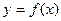 , (где
, (где 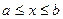 ), отрезком ab оси Ох и отрезками прямых
), отрезком ab оси Ох и отрезками прямых 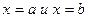 (рис. 23), вычисляется по формуле:
(рис. 23), вычисляется по формуле:
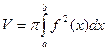 | (3) |
Пример 15. Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной параболой 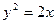 , прямой
, прямой 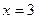 и осью Ох (рис. 24)
и осью Ох (рис. 24)
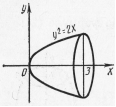 Рис. 24 Рис. 24 | 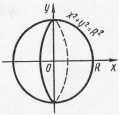 Рис. 25 Рис. 25 |
Решение: Применяя формулу (3), находим:
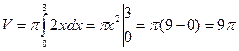 ;
;
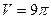 куб. ед.
куб. ед.
Пример 16. Вычислить объем шара радиуса R (рис. 25).
Решение: Шар образован вращением вокруг оси Ох круга, ограниченного окружностью 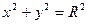 с центром в начале координат и радиусом R. Учитывая симметрию круга относительно оси ординат, сначала найдем по формуле (3) половину искомого объема:
с центром в начале координат и радиусом R. Учитывая симметрию круга относительно оси ординат, сначала найдем по формуле (3) половину искомого объема:
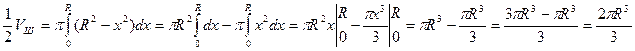 ;
; 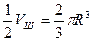 куб. ед.
куб. ед.
Следовательно, 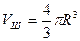 куб. ед.
куб. ед.
Пример 17. Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной осью Ох и полуволной синусоиды 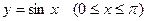 (рис. 26).
(рис. 26).
Решение: Применяя формулу (3), находим:
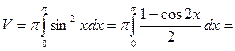
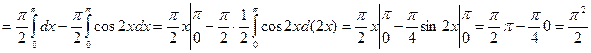 ;
;
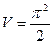 куб. ед.
куб. ед.
 Рис. 26 Рис. 26 | 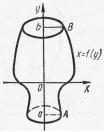 Рис. 27 Рис. 27 |
Объем тела, образованного вращением вокруг оси Оу криволинейной трапеции aABb, ограниченной непрерывной кривой 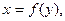 (где
(где 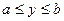 ), отрезком ab оси Оу и отрезками прямых
), отрезком ab оси Оу и отрезками прямых 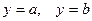 (рис. 27), вычисляется по формуле:
(рис. 27), вычисляется по формуле:
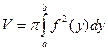 | (4) |
Пример 18. Вычислить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной параболой 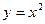 и прямой
и прямой 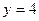 (рис. 28).
(рис. 28).
Решение: Применяя формулу (4), находим:
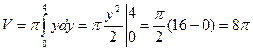 ;
; 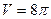 куб. ед.
куб. ед.
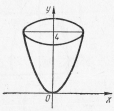 Рис.28 Рис.28 | 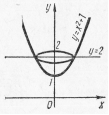 Рис. 29 Рис. 29 |
Пример 19. Вычислить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной параболой 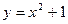 и прямой
и прямой 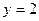 (рис. 29).
(рис. 29).
Решение: Объем полученного тела (оно называется параболоидом) вычислим по формуле(4):
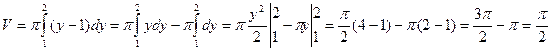 ;
; 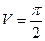 куб. ед.
куб. ед.
Путь, пройденный точкой. Если точка движется прямолинейно и ее скорость 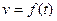 есть известная функция времени t, то путь, пройденный точкой за промежуток времени
есть известная функция времени t, то путь, пройденный точкой за промежуток времени 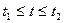 , вычисляется по формуле:
, вычисляется по формуле:
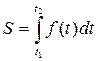 | (5) |
Пример 20. Тело движется прямолинейно со скоростью 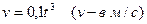 . Вычислить путь, пройденный телом за 10 с.
. Вычислить путь, пройденный телом за 10 с.
Решение: Применяя формулу (5), находим:
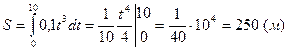 .
.
Пример 21. Скорость прямолинейно движущегося тела равна 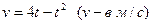 . Вычислить путь, пройденный телом от начала движения до остановки.
. Вычислить путь, пройденный телом от начала движения до остановки.
