Лабораторная работа № 8. Дифференциальное исчисление функций одной переменной
Дифференциальное исчисление функций одной переменной
Теоретический минимум
1. Определение производной функции в точке.
2. Геометрический смысл производной.
3. Механический смысл производной.
4. Правила дифференцирования: производная алгебраической суммы, произведения и частного.
5. Производная параметрически заданной функции.
6. Производная сложной функции.
7. Производные основных элементарных функций.
8. Уравнение касательной к графику функции.
9. Уравнение нормали к графику функции.
10. Правило Лопиталя.
Задания
1. Вычислить производную функции 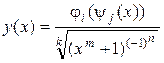 , где функции ji(x) и yj(x) находятся из таблиц:
, где функции ji(x) и yj(x) находятся из таблиц:
| i | ||||||||
| ji(x) | sin x | cos x | tg x | ctg x | arc sin x | arc cos x | arc tg x | arc ctg x |
| j | ||||
| yj(x) | аx k | a x | log a x | аln x |
а значения параметров а, k, m, n и индексов i и j определяются в соответствии с вариантом работы:
| № | a | k | m | n | i | j | № | a | k | m | n | i | j |
2. Составить уравнения касательной и нормали к графику функции y (x) = 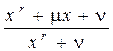 при x = n, где значения r, m, n определяются в соответствии с вариантом работы:
при x = n, где значения r, m, n определяются в соответствии с вариантом работы:
| № | r | m | n | № | r | m | n | № | r | m | n |
| – 3 | – 1 | ||||||||||
| – 2 | |||||||||||
| – 1 | – 3 | – 3 | |||||||||
| – 4 | – 2 | – 5 | |||||||||
| – 5 | – 1 | – 6 | – 3 | ||||||||
| – 6 | – 5 | – 7 | – 2 | ||||||||
| – 7 | – 3 | – 6 | – 9 | – 1 | |||||||
| – 9 | – 2 | – 7 | |||||||||
| – 1 | – 9 | – 3 | |||||||||
| – 2 | – 4 |
3. Составить уравнения касательной и нормали к графику функции y = y(x), заданной параметрически: 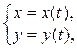 в точке М(х(t0); y(t0)), где x(t), y(t) и t0 определяются в соответствии с вариантом работы:
в точке М(х(t0); y(t0)), где x(t), y(t) и t0 определяются в соответствии с вариантом работы:
| № | x(t) | y(t) | t0 |
| 4×sin 3t | 4×cos 3t | p/3 | |
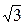 ×cos t ×cos t | sin t | p/3 | |
| 5×(t – sin t) | 5×(1– cos t) | p/3 | |
| 2t – t 2 | 3t – t 3 | ||
| cos t + sin t | sin 2t | p/4 | |
arc sin 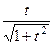 | arc cos 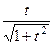 | – 1 | |
| t×(t×cos t – 2×sin t) | t×(t×sin t + 2×cos t) | p/4 | |
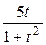 | 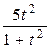 | ||
| 1 + 2×ln ctg t | tg t + ctg t | p/4 | |
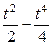 | 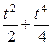 | ||
| 3t×cos t | 3t×sin t | p/2 | |
| sin2t | cos2t | p/6 | |
arc cos 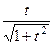 | arc sin 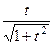 | ||
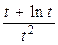 | 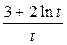 | ||
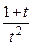 | 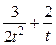 | ||
| 6×sin4t | 6×cos4t | p/6 | |
| 3(t×sin t + cos t) | 3(sin t – t×cos t) | p/4 | |
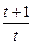 | 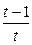 | – 1 | |
| 1 – t 2 | 1 – t 3 | ||
| ln(1 + t 2) | t – arc tg t | ||
| t – t×sin t | t×cos t | ||
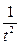 | 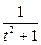 | ||
| 3×cos t | 4×sin t | p/4 | |
| t – t 4 | t 2– t 3 | ||
| t 3 + 1 | t 2+ t + 1 | ||
| 2cos t | sin t | p/3 | |
| 2tg t | 2sin2t + 2sin 2t | p/4 | |
| t 3 + 1 | t 2 | – 2 | |
| sin t | e t | ||
| sin t | cos 2t | p/6 |
4. Применяя правило Лопиталя, найти 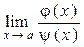 , если:
, если:
| № | j(x) | y(x) | a |
| x – arc tg x | x 3 | ||
| p – 2arc tg x | ln 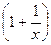 | 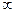 | |
| x – sin x | x – tg x | ||
| p – 2arc tg x | ln 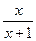 | 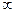 | |
| p – 2arc sin x | sin 3(x – 1) | ||
| e x – e –x | sin x × cos x | ||
| 1 – sin(px/2) | ln x | ||
| sin(px/2) | ln (1 – x) | ||
| x ln x – x + 1 | (x – 1)×ln x | ||
| a 2 – x 2 | ctg 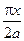 | a | |
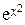 – 1 – 1 | cos x – 1 | ||
| ln(sin 2x) | ln(sin x) | ||
| x×cos x – x×sin x | x×sin x | ||
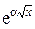 – 1 – 1 | 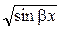 | ||
| a x – b x | 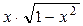 | ||
| 1 – cos 2x | cos 7x – cos 3x | ||
| ln x | 1 + 2ln(sin x) | +0 | |
| e 3x – 3x – 1 | sin2 5x | ||
| cos x × ln(x – 3) | ln (e x – e 3) | 3 + 0 | |
| tg(px/2) | ln(1 – x) | 1 – 0 | |
| e x – e –x – 2x | x – sin x | ||
| e 2x – 1 | arc sin x | ||
| e x – 1 – x |  x×(e x – 1) x×(e x – 1) | ||
| (x – 2p)2 | tg(cos x – 1) | 2p | |
| cos x | 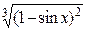 | p/2 | |
| 1– sin x | (p/2 – x)2 | p/2 | |
| tg x – x | sin x – x | ||
1 – 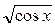 | sin x | ||
| ln x | x a | ¥ | |
| ln(1 + x 2) | ln(p/2 – arc tg x) | ¥ |
Справочный материал
к 8-й лабораторной работе
1. Производная функцииу = у(х) по переменной х в точке х0 – конечный двусторонний предел отношения изменения значения функции у = у(х) к соответствующему бесконечно малому изменению значения аргумента х этой функции в окрестности точки х = х0: у¢ (х0) = 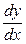 =
= 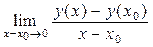 =
= 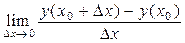 =
= 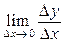 . Значение производной у¢ (х0) равно тангенсу угла наклона касательной к графику функции у = у(х) при х = х0 относительно положительного направления координатной оси х. Если s(t) – зависимость перемещения материальной точки от времени, то s¢ (t) =
. Значение производной у¢ (х0) равно тангенсу угла наклона касательной к графику функции у = у(х) при х = х0 относительно положительного направления координатной оси х. Если s(t) – зависимость перемещения материальной точки от времени, то s¢ (t) = 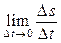 = v(t) – мгновенная скорость этой материальной точки в момент времени t.
= v(t) – мгновенная скорость этой материальной точки в момент времени t.
2. Дифференцируемость функцииу = у(х): если в каждой точке х интервала (а; b) существует производная у¢(х), то функция у = у(х) называется дифференцируемой на этом интервале.
3. Правила дифференцирования – производная алгебраической суммы: (u ± v)¢ = u¢ ± v¢ ; (u ± v ± w)¢ = u¢ ± v¢ ± w¢ ; производная произведения: (u×v)¢ = u¢×v + u×v¢; (u×v×w)¢ = u¢×v×w + u×v¢×w + u×v×w¢ ; производная дроби: (u/ v)¢ = (u¢×v – u×v¢ )/ v2.
4. Производная параметрически заданной функцииx = x(t), y = y(t): y¢ (x) = y¢ (t) / x¢ (t).
5. Производная сложной функции: если y = u(v(w(x))), то 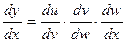 =
= 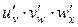 . Последовательность дифференцирования сложной функции обратна последовательности вычисления значения функции, в частности, на калькуляторе. Например, при вычислении значения функции у = sin2(ln(x3+
. Последовательность дифференцирования сложной функции обратна последовательности вычисления значения функции, в частности, на калькуляторе. Например, при вычислении значения функции у = sin2(ln(x3+ 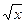 )) в точке х алгебраические операции выполняются в следующей последовательности: куб х, квадратный корень из х, сумма куба и квадратного корня, логарифм суммы, синус логарифма, квадрат синуса, следовательно, нахождение производной у¢ (х) сводится к произведению производных, определяемых в последовательности: производная квадрата синуса, производная синуса логарифма, производная логарифма суммы, производная суммы, равная сумме производных куба х и квадратного корня из х, т.е. каждая следующая дифференцируемая функция является аргументом предыдущей.
)) в точке х алгебраические операции выполняются в следующей последовательности: куб х, квадратный корень из х, сумма куба и квадратного корня, логарифм суммы, синус логарифма, квадрат синуса, следовательно, нахождение производной у¢ (х) сводится к произведению производных, определяемых в последовательности: производная квадрата синуса, производная синуса логарифма, производная логарифма суммы, производная суммы, равная сумме производных куба х и квадратного корня из х, т.е. каждая следующая дифференцируемая функция является аргументом предыдущей.
6. Таблица производных основных элементарных функций
| Вид функции | Формула функции | Производная функции |
| 1) Постоянная | y = C для всех х Î 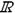 | С¢ = 0 |
| 2) Линейная | y = х, хÎ 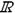 y = ах ± b, хÎ y = ах ± b, хÎ 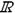 | х¢ =1R (ах ± b)¢ = а |
| 3) Степенная | y = х а, х > 0, а Î 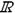 y = х – а, х > 0, а Î y = х – а, х > 0, а Î 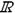 y= 1/х, х ¹0 y= 1/х, х ¹0 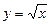 , х > 0 , х > 0 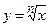 , х > 0, n Î , х > 0, n Î 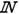 \ {1} \ {1} | (х а )¢ = аха – 1R (х– а )¢ = –ах – а –1 (1/х)¢ = –1/x2 ( 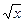 )¢ = 1/( )¢ = 1/( 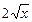 ) ( ) ( 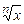 )¢ = 1/( )¢ = 1/( 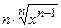 ) ) |
| 4) Показательная | y = а х, а > 0, а ¹1, х Î 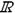 y =е х, х Î y =е х, х Î 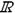 y =е – х, х Î y =е – х, х Î 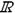 | (а х )¢ = а х×ln аR (е х )¢ =е х (е– х)¢ = – е– х |
| 5) Показательно-степенная | y = u(х) v(х) | (uv)¢ = (v×uv–1)×u¢ + (uv×ln u)×v¢ |
| 6) Логарифмическая | y =log а х, а > 0, а ¹1, х > 0 y =ln х, х > 0 | (log а х)¢ = 1/(x×ln a) (ln х)¢ =1/ х |
| 7) Тригонометрическая | y =sin x х Î 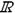 y =cos x х Î y =cos x х Î 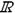 y = tg x х Î y = tg x х Î 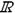 y = ctg x х Î y = ctg x х Î 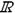 | (sin x)¢ = cos x (cos x)¢ = – sin x (tg x)¢ = 1/cos2x (ctg x)¢ = – 1/sin2 x |
| 8) Обратная тригонометрическая | y =arc sin x –1 £ х £ 1 y = arc cos x –1 £ х £ 1 y = arc tg x х Î 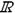 y = arc ctg x х Î y = arc ctg x х Î 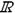 | (arc sin x)¢ = 1/ 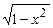 (arc cos x)¢ = – 1/ (arc cos x)¢ = – 1/ 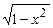 (arc tg x)¢ = 1/(1 + x2) (arc ctg x)¢ = – 1/(1 + x2) (arc tg x)¢ = 1/(1 + x2) (arc ctg x)¢ = – 1/(1 + x2) |
| 9) Гиперболическая | y =sh x х Î 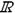 y =ch x х Î y =ch x х Î 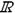 y = th x х Î y = th x х Î 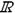 y = cth x х¹0 y = cth x х¹0 | (sh x)¢ = ch x (ch x)¢ = sh x (th x)¢ = 1/ch2x (cth x)¢ = – 1/sh2 x |
7. Уравнение касательнойк кривой у = у(х)в точке М(х0; у0), где y0 = y(x0): y = y0 + у'(х0)×(x – x0).
8. Уравнение нормали к кривой у= у(х)в точке М(х0; у0): y = y0 – 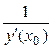 ×(x – x0).
×(x – x0).
9. Правило Лопиталя: 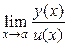 =
= 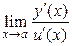 , где а – любое конечное число или ∞. Правило Лопиталя можно использовать только для неопределенностей вида
, где а – любое конечное число или ∞. Правило Лопиталя можно использовать только для неопределенностей вида 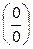 и
и 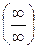 . Правило Лопиталя можно использовать многократно, если при его использовании снова возникает одна из указанных неопределенностей.
. Правило Лопиталя можно использовать многократно, если при его использовании снова возникает одна из указанных неопределенностей.
