Лабораторная работа № 4. Собственные значения и собственные векторы квадратной матрицы

Собственные значения и собственные векторы квадратной матрицы

Теоретический минимум

1. Линейная зависимость векторов.

2. Линейная независимость векторов.

3. Критерий линейной независимости векторов.

4. Базис пространства.

5. Ортогональный базис.

6. Ортонормированный базис.

7. Собственный вектор матрицы.

8. Собственное значение матрицы.

Задание

1. Найти собственные значения и собственные векторы матрицы A:

№	Матрица A	№	Матрица A	№	Матрица A

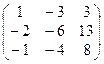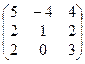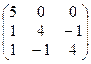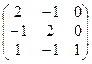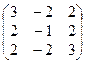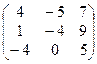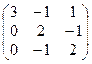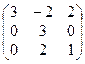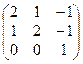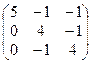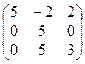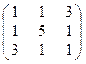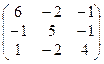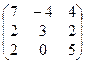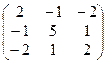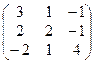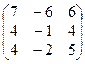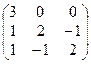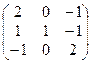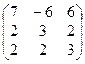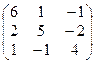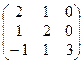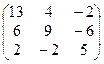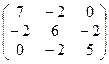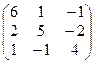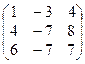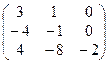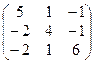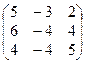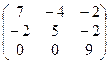Справочный материал

к 4-й лабораторной работе

1. Линейная комбинация векторов– сумма векторов с произвольными числовыми коэффициентами: λ₁∙a₁ + λ₂∙a₂ + … + λ_n∙a_n.

2. Линейно зависимые векторы– совокупность векторов, хотя бы один из которых может быть представлен в виде линейной комбинации остальных, в противном, векторы данной совокупности называются линейно независимыми.

3. Базис пространства – упорядоченная системамаксимально возможного числа линейно независимых векторов в этом пространстве. Число векторов, образующих базис пространства, определяет размерность этого пространства: в двумерном пространстве (на плоскости) в качестве базиса могут служить любые два неколлинеарных вектора, в трехмерном пространстве – любые три некомпланарных вектора.

4. Разложение вектора по базису пространства:представление вектора в виде линейной комбинации векторов базиса, так, если векторы q₁, q₂, … , q_n образуют базис в n-мерном пространстве, то любой вектор а в этом пространстве можно единственным образом представить в виде: a = а₁× q₁+ а₂× q₂+ … + а_n× q_n, при этом коэффициенты {a₁; a₂; …; a_n} называются координатами вектора a в этом базисе.

5. Критерий линейной независимостит векторов вп-мерном пространстве:т векторов (т £ п) являются линейно независимыми, если ранг матрицы, строки которой – координаты этих векторов в базисе их задания, равен т. В частности, п векторов в п-мерном пространстве линейно независимы, если определитель, строки которого – координаты этих векторов, не равен 0; если же этот определитель равен 0, то соответствующие п векторов линейно зависимы.

6. Ортогональный базис – базис пространства, состоящий из взаимно ортогональных векторов, т.е. для всех пар взаимно ортогональных векторов базиса скалярное произведение q_i×q_j= 0 (i ¹ j).

7. Нормирование вектора q – нахождение единичного вектора того же направления, что и вектор q: е = 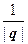q.

8. Ортонормированный базис – базис пространства, состоящий из взаимно ортогональных векторов единичной длины.

9. Собственный вектор и собственное значение матрицы:если в результате произведения квадратной матрицы А на ненулевой вектор-столбец p получается вектор-столбец lр, где l – число, т.е. если А×р = l×р, то р называется собственным вектором матрицы А, а число l – собственным значением этой матрицы.

10. Идентификация собственных векторов и собственных значений матрицы:

Ø собственные значения l квадратной матрицы А являются действительными корнями уравнения det (А – λE) = 0, где E – единичная матрица, порядок которой совпадает с порядком матрицы А;

Ø координаты собственного вектора р, относящегося к собственному значению λ, находятся из матричного уравнения (А – λE)р = 0, в котором р – вектор-столбец соответствующих координат собственного вектора матрицы А;

Ø собственный вектор матрицы, относящийся к собственному значению λ, определяется с точностью до произвольного числового коэффициента;

Ø собственные векторы, относящиеся к различным собственным значениям, линейно независимы;

Ø симметрическая матрица порядка п всегда имеет п действительных собственных значений с учетом их кратности;

Ø собственные векторы симметрической матрицы, относящиеся к различным собственным значениям, ортогональны между собой;

Ø линейная комбинация собственных векторов матрицы А, относящихся к кратному собственному значению λ, также является собственным вектором этой матрицы, поэтому такими линейными комбинациями исчерпываются все собственные векторы матрицы А, относящиеся к собственному значению λ.