Понятие функции (отображение)
Функция
В элементарной математике мы встречаемся с разными объектами, которые называются словом функция: логарифмическая функция, показательная функция, тригонометрическая функция и другие. Напомним основные факты, относящиеся к этим объектам.
Пусть 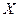 и
и 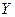 – некоторые множества. Будем говорить, что задана функция, определенная на
– некоторые множества. Будем говорить, что задана функция, определенная на 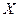 со значениями в
со значениями в 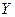 , если указан закон
, если указан закон 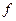 , сопоставляющий каждому элементу
, сопоставляющий каждому элементу 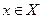 некоторый элемент
некоторый элемент 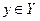 .
.
Так для числовых множеств 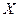 и
и 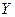 , если под
, если под 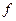 понимается функция
понимается функция 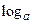 , то
, то 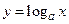 , если
, если 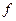 – функция
– функция 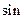 , то
, то 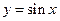 .
.
Множество 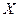 называется областью определения (областью существования) функции, а элементы этого множества называются аргументами или независимыми переменными.
называется областью определения (областью существования) функции, а элементы этого множества называются аргументами или независимыми переменными.
В простейшем случае 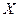 есть открытый промежуток (интервал)
есть открытый промежуток (интервал) 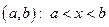 , или полуоткрытый промежуток (полуинтервал)
, или полуоткрытый промежуток (полуинтервал) 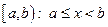 или
или 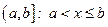 , где
, где 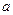 и
и 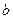 – некоторые числа или символы
– некоторые числа или символы 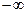 и
и 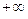 (в последних случаях равенства исключаются).
(в последних случаях равенства исключаются).
Элемент 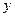 , соответствующий конкретному значению
, соответствующий конкретному значению  , называют значением функции от элемента
, называют значением функции от элемента  . При изменении аргумента
. При изменении аргумента  значение
значение 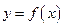 меняется по заданному закону, поэтому элемент
меняется по заданному закону, поэтому элемент 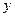 называют зависимой переменной.
называют зависимой переменной.
Множество значений 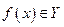 , которые принимает функция
, которые принимает функция 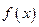 , когда
, когда  пробегает все
пробегает все 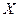 (
(  принимает все значения из
принимает все значения из 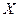 ) будем называть множеством значений или областью значений функции.
) будем называть множеством значений или областью значений функции.
Если  – некоторая точка
– некоторая точка 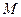 числовой оси, а соответствующее значение
числовой оси, а соответствующее значение 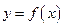 – точка
– точка 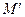 другой числовой оси, то функцию называют отображением точки
другой числовой оси, то функцию называют отображением точки 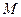 в точку
в точку 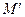 .
.
При этом 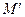 – образ точки
– образ точки 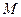 , а точка
, а точка 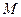 прообраз точки
прообраз точки 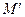 .
.
Таким образом, в зависимости от природы множеств 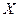 и
и 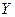 термин функция имеет ряд синонимов: отображение, преобразование, оператор и др. Наряду с обозначением
термин функция имеет ряд синонимов: отображение, преобразование, оператор и др. Наряду с обозначением 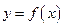 для функции используют и такие:
для функции используют и такие: 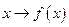 ,
, 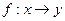 ,
, 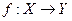 ,
, 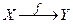 .
.
Итак, понятие функции состоит из трех частей:
1) области определения 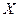 ;
;
2) множества 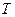 , содержащего область значений
, содержащего область значений 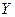 ;
;
3) правила, которое для каждого элемента 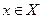 задает единственный элемент
задает единственный элемент 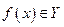 .
.
Суть дела изложена в пункте 3). Важно, что 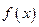 определено однозначно, т.е.одному элементу
определено однозначно, т.е.одному элементу 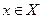 соответствует один элемент
соответствует один элемент 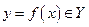 . Важно также, что значение
. Важно также, что значение 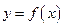 определено для каждого
определено для каждого  из
из 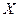 . Знание области определения
. Знание области определения 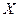 говорит о том, где «безопасно» применять функцию
говорит о том, где «безопасно» применять функцию 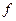 . В то же время необязательно знать точную область значений
. В то же время необязательно знать точную область значений 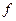 ; часто ее трудно описать, а мы хотим пользоваться функцией
; часто ее трудно описать, а мы хотим пользоваться функцией 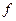 , не занимаясь подобными проблемами. Поясним слово «правило» в пункте 3). Пока будем считать, что знаем, что такое «правило»: некий способ получить
, не занимаясь подобными проблемами. Поясним слово «правило» в пункте 3). Пока будем считать, что знаем, что такое «правило»: некий способ получить 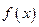 для заданного конкретного
для заданного конкретного  . Достаточно, чтобы
. Достаточно, чтобы 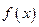 в принципе можно было вычислить по
в принципе можно было вычислить по  . Практически такое вычисление может оказаться невыполнимым: либо слишком трудоемким, требующим много времени, либо связанным с решением какой-то очень трудной задачи (все вышесказанное относительно слова «правило» относится и к основным элементарным функциям изучаемым в школе).
. Практически такое вычисление может оказаться невыполнимым: либо слишком трудоемким, требующим много времени, либо связанным с решением какой-то очень трудной задачи (все вышесказанное относительно слова «правило» относится и к основным элементарным функциям изучаемым в школе).
Если числовые множества 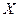 и
и 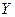 числовые множества, то
числовые множества, то 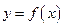 называется числовой функцией. Например,
называется числовой функцией. Например, 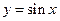 ,
, 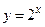 ,
, 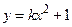 – числовые функции.
– числовые функции.
