Системы линейных алгебраических уравнений. 1. Определитель второго порядка задается равенством

Определители.

1. Определитель второго порядка задается равенством

.

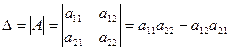2. Определитель третьего порядка задается равенством

.

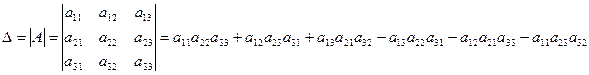3.Свойства определителей. 1. Определитель равен нулю, если он содержит: две одинаковые или пропорциональные строки; строку (столбец) из нулей. 2. Определитель не изменится, если к любой его строке прибавить другую строку, умноженную на некоторое число. 3.Разложение определителя по любой строке (столбцу):

.

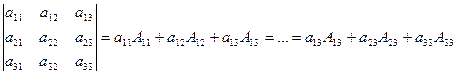Способы вычисления определителя третьего порядка.

а). Правило Саррюса (дополнения): б). Правило треугольников:

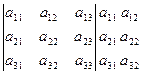
в). Разложение определителя по первой строке:

.

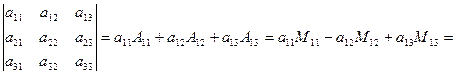
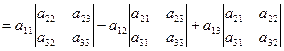Действия над матрицами. Обратная матрица.

1. Матрицей 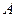порядка 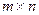называется прямоугольная таблица, составленная из действительных чисел и содержащая 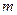строк и 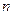столбцов:

.

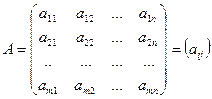2. Сумма (разность)матриц одного порядка = , .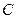

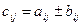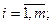
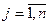3.Произведениематрицы на число .

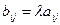
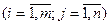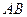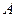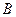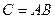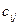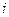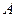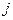4. Произведением матриц и называется матрица , элементы которой равны сумме произведений соответствующих элементов -ой строки матрицы и -го столбца матрицы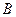

:

.

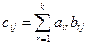
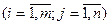При умножении матрицы порядка 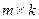на матрицу порядка 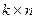получится матрица порядка .

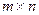Некоммутативность (неперестановочность) умножения матриц: .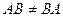

5. Если 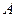- невырожденная квадратная матрица (определитель матрицы 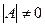), то существует единственная матрица 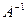, называемая обратной к матрице 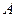, такая, что 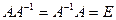, где 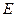- единичная матрица.

Чтобы найти 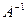необходимо: - вычислить определитель 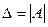матрицы 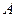; - найти алгебраические дополнения 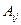каждого элемента 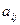матрицы 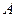; - составить из чисел 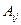матрицу 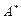; - транспонируя матрицу 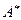, составить матрицу 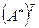; - умножить матрицу 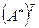на число 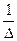: 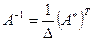; - делаем проверку .

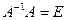Системы линейных алгебраических уравнений.

Система линейных уравнений третьего порядка имеет вид

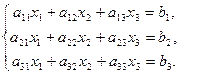
1. Правило Крамера: если определитель матрицы системы не равен 0, то система имеет единственное решение, которое определяется по формулам

, , ,

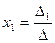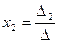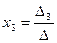где 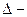определитель матрицы системы; 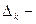определитель, получаемый из определителя 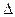заменой 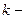го столбца столбцом свободных членов, .

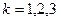2. Матричный способ:система линейных уравнений в матричной форме имеет вид 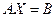, где

, , .

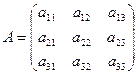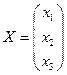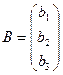Решение матричного уравнения определяется формулой .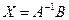

3.Метод Гауссазаключается в последовательном исключении неизвестных из уравнений системы. Для краткости вместо системы рассматриваем расширенную матрицу ее коэффициентов, которую приводим к треугольному виду:

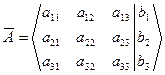
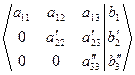
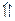
с помощью следующих, не меняющих решения, преобразований: 1.В можно менять местами строки.

2.Можно в менять местами столбцы слева от прямой черты. 3.К одной строке 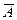можно прибавить другую, умноженную на некоторое число.

Треугольную матрицу записываем в виде уравнений снизу вверх, последовательно находя неизвестные.

Векторы.

Векторомназывается направленный отрезок.

Координаты векторас началом в точке 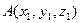и концом в точке :

.

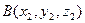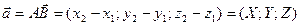Длина вектора:

.

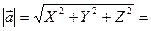
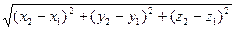Проекция вектора на ось u: 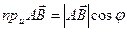, 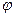- угол между осью 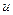и вектором 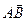. Направляющие косинусы: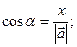 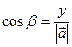;;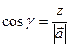 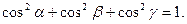Сумма (разность) векторов 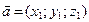и 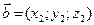: 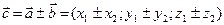. Произведение вектора 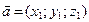на число : .

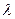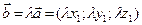Условие коллинеарности векторов: .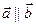

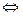
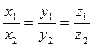Разложение вектора 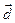по векторам 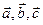: 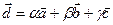, где 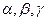- координаты вектора 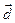в системе координат .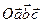