Системы линейных алгебраических уравнений

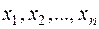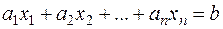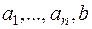Общие понятия. Линейным (относительно неизвестных ) называют алгебраическое уравнение первой степени, т.е. уравнение вида , где – числа. Система 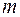линейных уравнений с 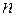неизвестными имеет вид

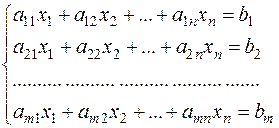(6)

В общем случае число уравнений в системе не обязательно совпадает с числом неизвестных: 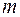может быть меньше, равно или больше числа .

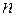Числа 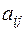(вещественные или комплексные) называются коэффициентами системы (6); 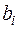– свободными членами; 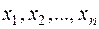– неизвестными.

Систему (6) можно записать в матричной форме:

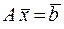, (7)

где , , .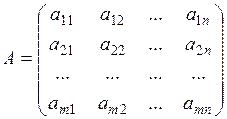

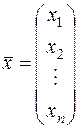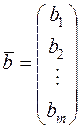Если 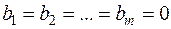, то система называется однородной, в противном случае она называется неоднородной. Матрицу называют матрицей системы (6). Расширенной матрицей системы (6) линейных уравнений называют матрицу , к которой добавлен (справа) столбец свободных членов 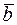. Такую матрицу будем обозначать в дальнейшем символом .

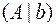Определение. Совокупность 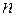чисел 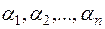называется решением системы (6), если после замены неизвестных 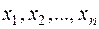числами 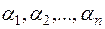соответственно каждое из уравнений системы превращается в верное равенство.

Пример 11. Рассмотрим систему линейных уравнений

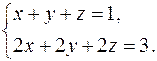
Эта система 2-х уравнений с тремя неизвестными решений не имеет, так как любая тройка чисел, удовлетворяющая первому уравнению, не может удовлетворять второму.

Пример 12. Система

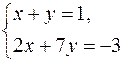
имеет единственное решение , .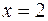

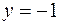Пример 13. Рассмотрим систему линейных уравнений

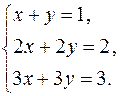
Пара чисел 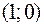есть одно из решений этой системы трех уравнений с двумя неизвестными, 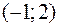– другое решение. Эта система имеет бесконечно много решений: значения 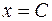, 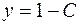при любом действительном значении 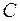удовлетворяют данной системе.

Рассмотренные примеры систем линейных уравнений показывают, что, вообще говоря, система может либо вовсе не иметь решений, либо иметь единственное решение, либо иметь их несколько (в последнем случае, оказывается, система всегда имеет бесконечное множество решений).

Определение. Система линейных уравнений, не имеющая ни одного решения, называется несовместной. Система, обладающая хотя бы одним решением, называется совместной.

Относительно каждой системы линейных уравнений могут быть поставлены следующие вопросы:

1) Совместна заданная система или нет?

2) В случае, если система совместна, как определить, сколько она имеет решений – одно или несколько?

3) Как найти все решения системы?

Ответ на все эти вопросы дает теория систем линейных уравнений.

Правило Крамера. Ограничимся сначала рассмотрением систем, у которых число уравнений равно числу неизвестных (такие системы называют квадратными).

Пусть дана система 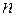линейных уравнений с 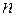неизвестными:

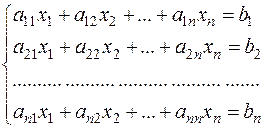(8)

Определитель

,

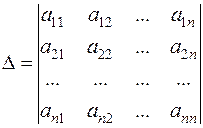составленный из коэффициентов при неизвестных, называется определителем системы (8).

Теорема. Если определитель 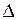квадратной системы (6) отличен от нуля, то эта система имеет единственное решение. Это решение может быть найдено по формулам

,

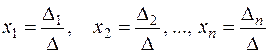где 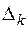– определитель, получаемый из определителя 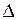заменой 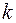-го столбца на столбец свободных членов.

(Без доказательства)

Формулы для неизвестных носят название формул Крамера.

Пример 14. Решить систему линейных уравнений методом Крамера:

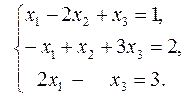
Вычислим определитель матрицы системы:

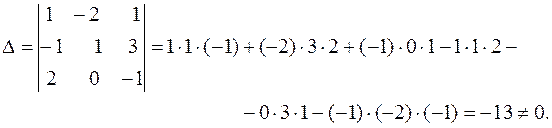
Значит, система имеет единственное решение. Вычислим определители

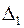Определитель получается из определителя 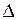заменой 1-го столбца столбцом свободных членов.

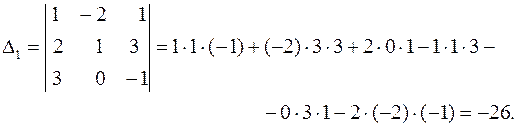
Определитель 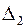получается из определителя 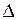заменой 2-го столбца столбцом свободных членов.

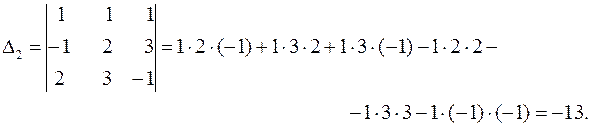
Заменим в определителе 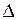3-ий столбец столбцом свободных членов и вычислим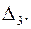

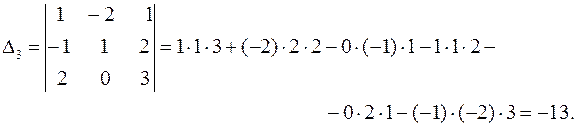
Решение системы находим по формулам:

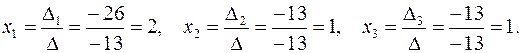
Ответ. (2; 1;1)

Метод Гаусса (метод последовательного исключения неизвестных) решения систем линейных уравнений. Под элементарными преобразованиями системы линейных уравнений понимаются следующие операции:

1) умножение какого-либо уравнения системы на число, отличное от нуля;

2) прибавление к одному уравнению другого уравнения;

3) перемена местами уравнений в системе.

Комбинируя элементарные преобразования первого и второго типов, мы можем к любому уравнению прибавить другое уравнение, умноженное на произвольное число.

Производя элементарные преобразования в системе, мы получаем новую систему. Очевидно, что каждому элементарному преобразованию системы соответствуют аналогичные преобразования над строками расширенной матрицы этой системы и, наоборот, каждому элементарному преобразованию строк расширенной матрицы соответствует некоторое элементарное преобразование в системе. Таким образом, элементарные преобразования в системе сводятся к соответствующим преобразованиям над строками ее расширенной матрицы.

Определение. Две системы линейных уравнений от одних и тех же неизвестных называются равносильными, если каждое решение одной из них является решением другой, и наоборот (или если обе системы несовместны).

Заметим, что число уравнений в равносильных системах может быть различным.

Теорема. При элементарных преобразованиях система линейных уравнений переходит в равносильную систему.

(Без доказательства)

Сущность метода Гаусса заключается в том, что с помощью элементарных преобразований система уравнений приводится к такому виду, чтобы матрица системы оказалась треугольной. Для упрощения изложения мы будем иметь дело не с самой системой (6), а с расширенной матрицей этой системы (производя при этом элементарные преобразования только над строками матрицы).

Пример 15.Решить систему уравнений методом Гаусса

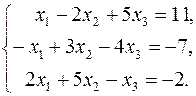
Запишем расширенную матрицу системы.

.

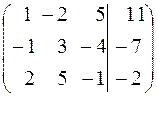Нашей целью является приведение матрицы к треугольному виду. Для этого будем выполнять элементарные преобразования над строками матрицы. Первую строку выбираем в качестве ведущей (у нее элемент 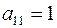). К элементам первой строки прибавим соответствующие элементы второй строки, а от третьей строки отнимем первую, умноженную на 2. Получим систему, равносильную данной:

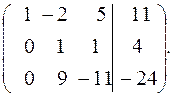
Вычтем из третьей строки вторую, умноженную на 9:

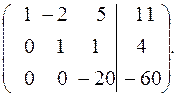
Получили систему треугольного вида. Из последней строки матрицы получаем уравнение 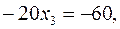из которого находим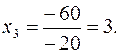

Второй строке матрицы соответствует уравнение: 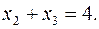Подставляя найденное значение 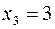в это уравнение, получаем 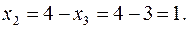Подставляя в первое уравнение системы 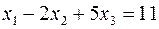значения 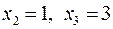получаем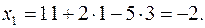

Ответ: (−2; 1; 3).

Критерий совместности системы линейных уравнений. Рассмотрим снова произвольную систему 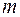линейных уравнений с 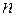неизвестными, которую запишем, как и раньше, в матричной форме (7).

Очевидно, что ранги матриц и 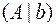связаны неравенством .

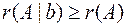Вопрос о совместности системы (7) полностью решается следующей теоремой.

Теорема Кронекера-Капелли. Для того чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг матрицы этой системы был равен рангу ее расширенной матрицы, т.е. чтобы .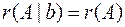

(Без доказательства)

Если совместность системы линейных уравнений установлена, то возникает вопрос о том, сколько она имеет решений. Ответ о числе решений системы линейных уравнений дает следующая теорема

Теорема (о числе решений). Пусть для системы 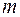линейных уравнений с 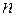неизвестными выполнено условие совместности, т.е. ранг 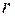матрицы системы равен рангу ее расширенной матрицы. Тогда, если ранг матрицы системы равен числу неизвестных ( 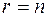), то система имеет единственное решение. Если же ранг матрицы системы меньше числа неизвестных ( 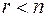), то система имеет бесконечное множество решений, а именно: некоторым 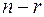неизвестным можно придавать произвольные значения, тогда оставшиеся 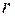неизвестных определятся уже единственным образом.

(Без доказательства)

Пример 16.Решить систему уравнений методом Гаусса, предварительно исследовав ее на совместность:

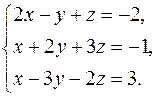
Запишем систему уравнений в виде расширенной матрицы:

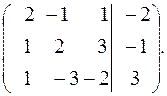
Поменяем местами первую и вторую строки матрицы:

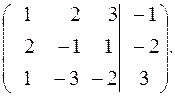
Первую строку матрицы будем считать ведущей (первый элемент строки равен 1), она не будет меняться при преобразованиях. Будем стремиться привести матрицу к треугольному виду. Для того чтобы в первом столбце матрицы получить нули, выполним следующие преобразования: из второй строки вычтем первую, умноженную на 2, а от третьей вычтем первую. Получим матрицу, равносильную данной:

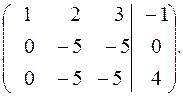
Чтобы получить матрицу треугольного вида, необходимо вычесть из третьей строки вторую. Окончательно получаем:

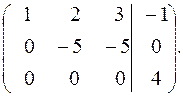
Ранг расширенной матрицы системы равен 3, ранг основной матрицы системы равен 2, т.е. 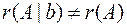, следовательно, система несовместна.

Пример 17.Решить систему уравнений методом Гаусса, предварительно исследовав ее на совместность:

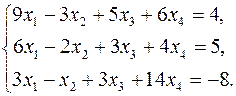
Запишем систему уравнений в виде расширенной матрицы:

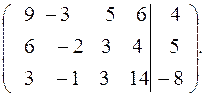
Поменяем местами первую и третью строки матрицы:

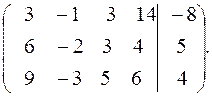
Будем приводить матрицу к треугольному виду, для этого выполним следующие преобразования: первая строка будет ведущей, а от второй строки вычтем первую, умноженную на 2, а из третьей вычтем первую, умноженную на 3. Получим равносильную систему:

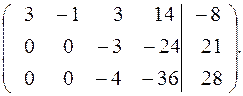
Умножим вторую строку на 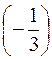, третью на 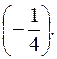При этом получим матрицу

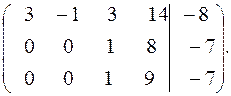
Вычтем из третьей строки вторую и получим матрицу треугольного вида.

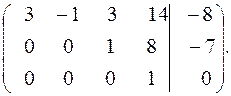
Ранг расширенной матрицы системы равен рангу матрицы системы, т.е. 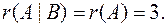Сравним ранг матрицы с числом неизвестных системы: 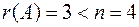. Согласно теореме о числе решений система имеет бесконечное множество решений. Найдем их.

Из последней строки матрицы треугольного вида имеем 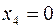, третьей строке соответствует уравнение 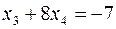. Зная 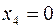, получаем Первой строке матрицы соответствует уравнение: 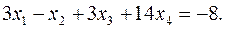Подставляя в это уравнение 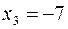, 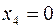получим уравнение 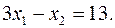Пусть 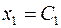, тогда .

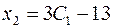Ответ: