Методические указания по выполнению контрольных работ
Примеры решения задач
ПРИМЕР №1
Даны два множества А= 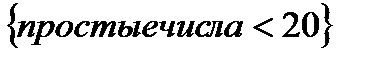
 и B=
и B= 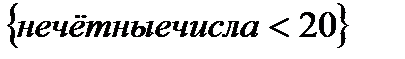 .Найти следующие множества: а) А
.Найти следующие множества: а) А 
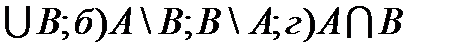 .
.
Решение.Множества A и B – конечные и легко перечислить их элементы: A= 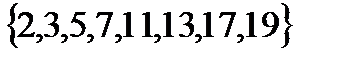 B=
B= 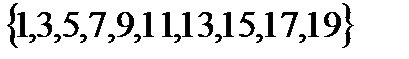 . Так как объединению множеств A и B принадлежат элементы, входящие в A или B, при этом одинаковые элементы зачисляются только один раз, то A
. Так как объединению множеств A и B принадлежат элементы, входящие в A или B, при этом одинаковые элементы зачисляются только один раз, то A 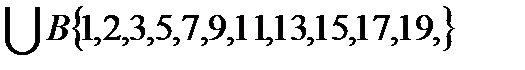 .По определению в множество A\B должны входить те элементы множества A ,которые не принадлежат множеству B . Поэтому A\B=
.По определению в множество A\B должны входить те элементы множества A ,которые не принадлежат множеству B . Поэтому A\B= 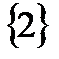 . Аналогично, множество B\A=
. Аналогично, множество B\A= 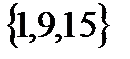 . Пересечению множеств принадлежат элементы, входящие одновременно в множество A и в множество B. Следовательно, A
. Пересечению множеств принадлежат элементы, входящие одновременно в множество A и в множество B. Следовательно, A 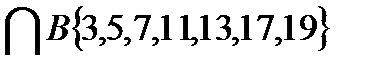 .
.
ПРИМЕР№2
.Даны множества на числовой прямой A= 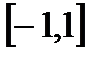 ; B=
; B= 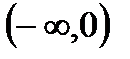 ; C=
; C= 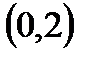 .
.
Найти следующие множества: А 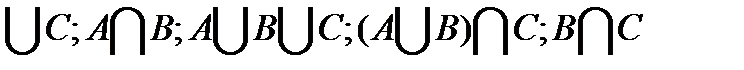 и изобразить их на числовой оси.
и изобразить их на числовой оси.
Решение.Множество A 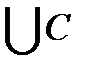 состоит из точек числовой прямой ,которые принадлежат либо множеству A ,либо множеству C:
состоит из точек числовой прямой ,которые принадлежат либо множеству A ,либо множеству C:
A 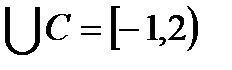 .
.
Множество A 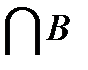 состоит из точек числовой прямой, которые принадлежат одновременно и множеству A и множеству B.
состоит из точек числовой прямой, которые принадлежат одновременно и множеству A и множеству B.
A 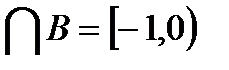 .
.
Множество A 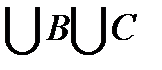 состоит из точек числовой прямой, которые принадлежат хотя бы одному из множеств A, B или C.
состоит из точек числовой прямой, которые принадлежат хотя бы одному из множеств A, B или C.
A 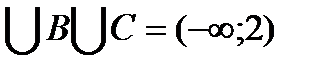 .
.
Множество (A 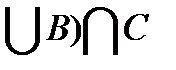 состоит из точек числовой прямой, которые принадлежат одновременно множеству A
состоит из точек числовой прямой, которые принадлежат одновременно множеству A 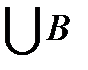 и множеству C. Построим множество A
и множеству C. Построим множество A 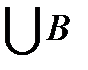 :
:
A 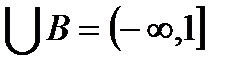
Построим здесь же множество (A 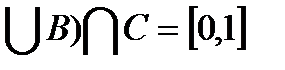
Множество B 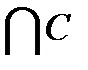 состоит из точек числовой прямой, которые принадлежат одновременно и множеству B и множеству C.
состоит из точек числовой прямой, которые принадлежат одновременно и множеству B и множеству C.
B 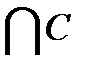 = Ø так как у этих множеств нет общих точек.
= Ø так как у этих множеств нет общих точек.

Пример № 3 . Найти производные функций
а) 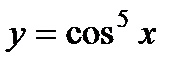 .
.
Пользуясь правилами дифференцирования и таблицей производных, получим:
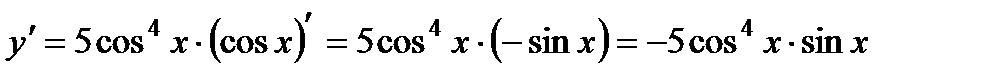 .
.
б) 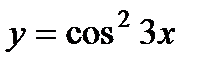 ;
;
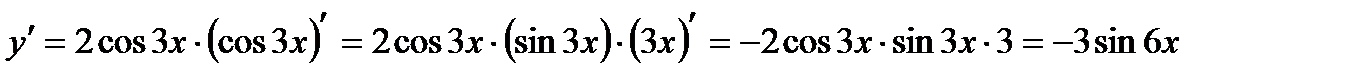 .
.
Пример №4 .Выполнить часть общего исследования функций:
А) Исследовать характер разрыва следующей функции 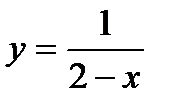 Функция имеет разрыв в точке
Функция имеет разрыв в точке 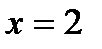 , где она не определена.
, где она не определена.
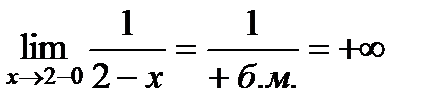 ;
; 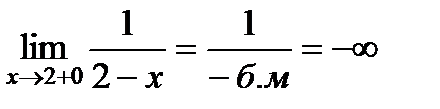 .
.
Односторонние пределы не существуют, следовательно, имеем разрыв второго рода. Через точку разрыва проходит вертикальная асимптота (рис. 2).
| y |
| x |
| y |
| XВ продукции кондитерской |
| A |
| A1 |
| C |
Рис 2. Рис 3.
Б) Найти экстремум функции 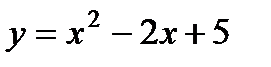 .
.
Найдем производную функции. Она равна 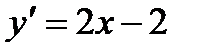 . Приравниваем производную к нулю
. Приравниваем производную к нулю 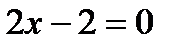 и находим критическую точку
и находим критическую точку 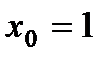 . Чтобы найти ординату этой точки, подставим
. Чтобы найти ординату этой точки, подставим 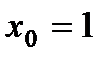 в данную функцию
в данную функцию 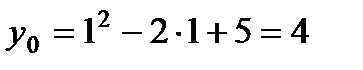 и запишем вершину параболы C(1; 4). Ось симметрии проходит через C параллельно оси
и запишем вершину параболы C(1; 4). Ось симметрии проходит через C параллельно оси 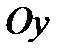 (рис. 3). Пересечение параболы с осью
(рис. 3). Пересечение параболы с осью 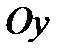 :
: 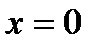 ;
; 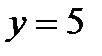 , т.е. A(0; 5). Симметричная ей точка A1(2; 5).
, т.е. A(0; 5). Симметричная ей точка A1(2; 5).
В) Найти точки экстремума и интервалы монотонности функции 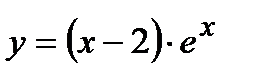 .
.
Находим первую производную:
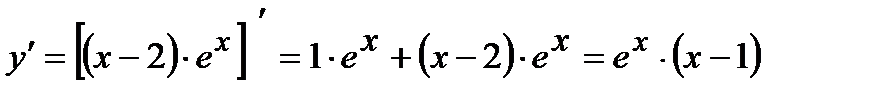 и приравниваем ее к нулю
и приравниваем ее к нулю 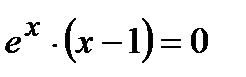 . Так как
. Так как 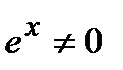 , то
, то 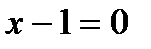 и
и 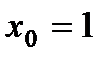 . Критическая точка
. Критическая точка 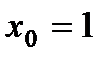 делит
делит 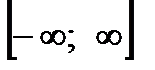 на два интервала монотонности,
на два интервала монотонности, 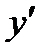 при переходе через точку
при переходе через точку 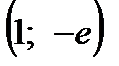 меняет знак с
меняет знак с 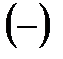 на
на 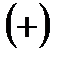 . Следовательно,
. Следовательно, 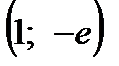 - точка минимума.
- точка минимума.
Пример № 5. Найти неопределенные интегралы:
а) 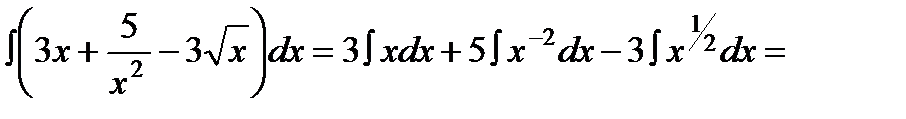
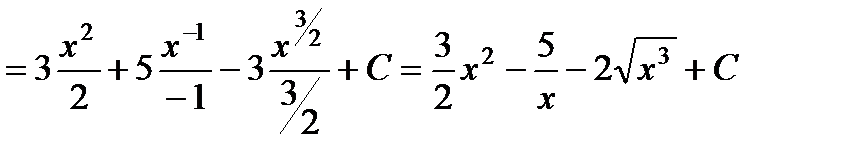 .
.
б) 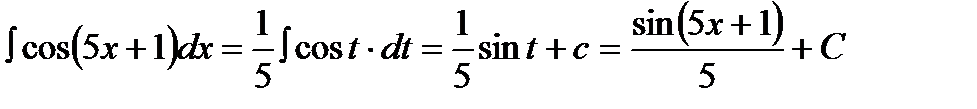 .
.
Здесь сделана замена: 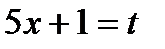 ;
; 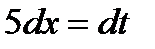 ;
; 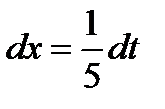 .
.
в) 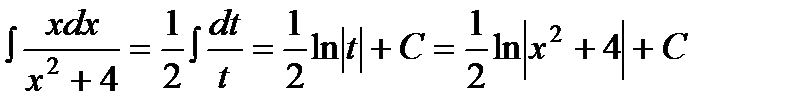 .
.
Сделана замена: 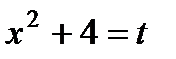 ;
; 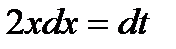 ;
; 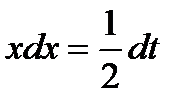 .
.
.
5. ЗАДАЧИ КОНТРОЛЬНОЙ РАБОТЫ.
Задание № 1 Даны множества на числовой прямой А,В и С Найти множества А 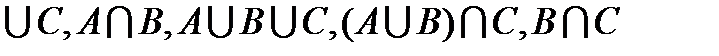 и изобразить их на числовой оси.
и изобразить их на числовой оси.
Варианты:
1. А= 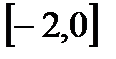 , В=
, В= 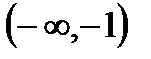 , С=
, С= 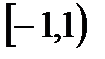
2. А= 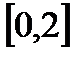 , В=
, В= 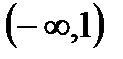
 , С=
, С= 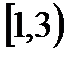
3. А= 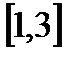 , В=
, В= 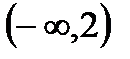 , С=
, С= 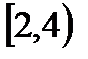
4. А= 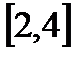 , В=
, В= 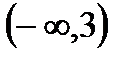 , С=
, С= 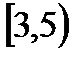
5. А= 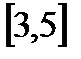 , В=
, В= 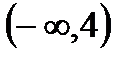 , С=
, С= 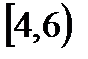
6. А= 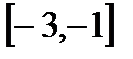 , В=
, В= 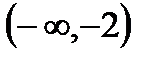 , С=
, С= 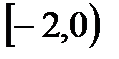
7. А= 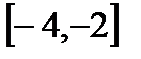 , В=
, В= 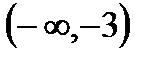 , С=
, С= 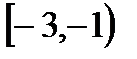
8. А= 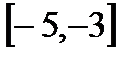 , В=
, В= 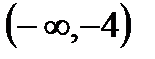 , С=
, С= 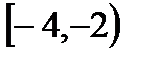
9. А= 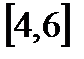 , В=
, В= 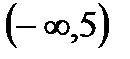 , С=
, С= 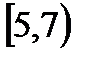
10.А= 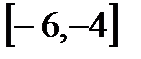 , В=
, В= 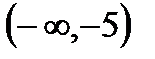 , С=
, С= 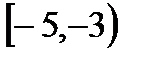
Задание № 2. Найти производные функций:
1) а) 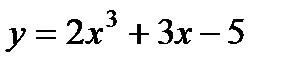 ; б)
; б) 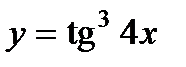 .
.
2) а) 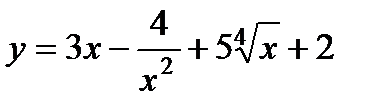 ; б)
; б) 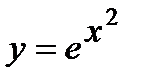 .
.
3) а) 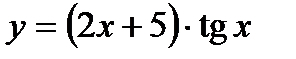 ; б)
; б) 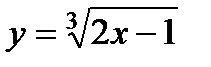 .
.
4) а) 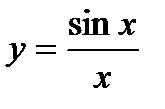 ; б)
; б) 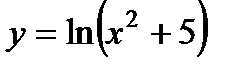 .
.
5) а) 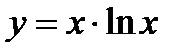 ; б)
; б) 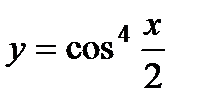 .
.
6) а) 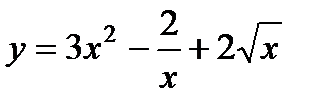 ; б)
; б) 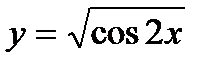 .
.
7) а) 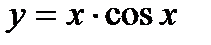 ; б)
; б) 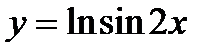 .
.
8) а) 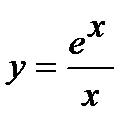 ; б)
; б) 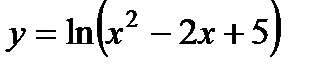 .
.
9) а) 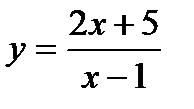 ; б)
; б) 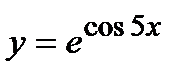 .
.
10) а) 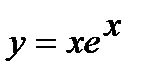 ; б)
; б) 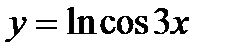 .
.
Задание № 3. Выполнить исследование функции по следующей схеме:
1) найти область определения;
2) проверить четность, нечетность функции;
3) найти точки пересечения с осями координат;
4) найти экстремумы функции и интервалы монотонности;
5) найти точки перегиба и интервалы выпуклости и вогнутости;
6) построить график функции.
1) 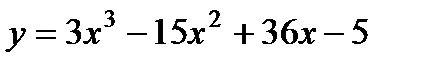 . 6)
. 6) 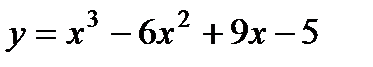 .
.
2) 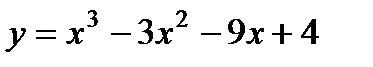 . 7)
. 7) 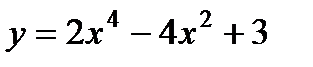 .
.
3) 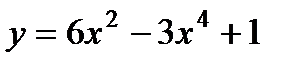 . 8)
. 8) 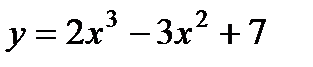 .
.
4) 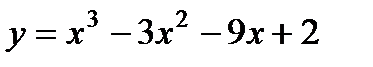 . 9)
. 9) 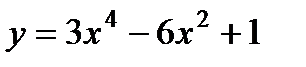 .
.
5) 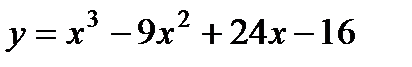 . 10)
. 10) 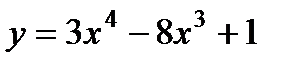 .
.
Задание № 4. Найти неопределенные интегралы. Результаты проверить дифференцированием.
1а) 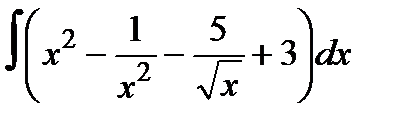 ;
;
2а) 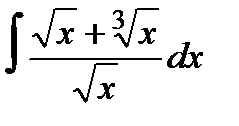 ;
;
3а) 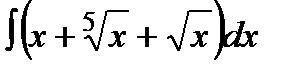 ;
;
4а) 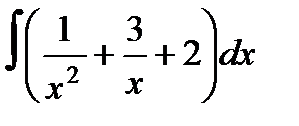 ;
;
5а) 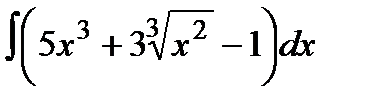 ;
;
6а) 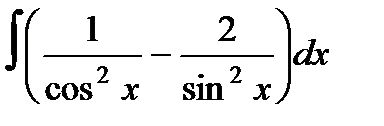 ;
;
7а) 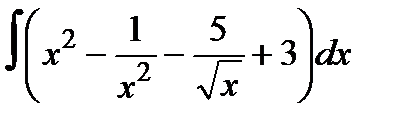 ;
;
8а) 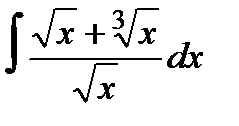 ;
;
9а) 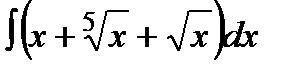 ;
;
10а) 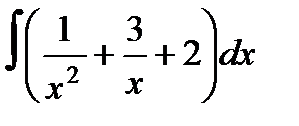 .
.
Задание №5:
1. 1. На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3 с яблоками. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с яблоками.
2. В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.
3. Петя, Катя, Ваня, Даша и Наташа бросили жребий, кому начинать игру. Найдите вероятность того, что начинать игру должен будет мальчик.
4. В каждой десятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Варя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Варя не найдет приз в своей банке.
5. В среднем на 50 исправных фонариков приходится два неисправных. Найдите вероятность купить работающий фонарик.
6. В мешке содержатся жетоны с номерами от 2 до 51 включительно. Какова вероятность, того, что номер извлеченного наугад из мешка жетона является однозначным числом?
7. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд будет первой владеть мячом. Команда А должна сыграть два матча — с командой В и с командой С. Найдите вероятность того, что в обоих матчах первой мячом будет владеть команда А.
8. На каждые 1000 электрических лампочек приходится 5 бракованных. Какова вероятность купить исправную лампочку?
9. На соревновании по метанию ядра приехали 2 спортсмена из Великобритании, 2 из Испании, 4 из Швеции. Порядок выступления определяется жребием. Найдите вероятность того, что Восьмым будет выступать спортсмен из Испании?
10. В сборнике билетов по физике всего 20 билетов, в 6 из них встречается вопрос по электростатике. Найдите вероятность того, что в случайно выбранном на экзамене билете ученику встретиться вопрос по электростатике.
ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ
1. Множества, элементы множества Операции над множествами. Числовые множества. Изображение множеств.
2. Понятие функции одной переменной. Предел функции в точке и на бесконечности Свойства пределов. Первый и второй замечательные пределы.
3. Непрерывность функции Классификация точек разрыва..
4. Понятие производной функции, её геометрический смысл. Правила дифференцирования. Таблица основных производных.
5. Возрастание и убывание функции ,экстремум функции Необходимое и достаточное условия экстремума функции. Выпуклость и вогнутость графика функции, точки перегиба. Необходимое и достаточное условия точки перегиба..
6. Использование производной для исследования функции и построения её графика.
7. Первообразная и неопределенный интеграл. Таблица основных интегралов. Основные методы интегрирования.
8. Определённый интеграл ,его геометрический смысл и основные свойства. Формула Ньютона-Лейбница..
9. Комбинаторика. Выборки элементов. Размещения, перестановки ,сочетания.
10. События и их классификация. Классическое и статистическое определение вероятности случайного события.
Список рекомендуемой литературы
1. Богомолов М.В. Практические занятия по математике.
2. Данко П.Е. Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. – М.: Высшая школа.
3. Григорьев С.Г. Математика: учебник для студентов сред. проф. учреждений / под ред. В.А. Гусева. – 2-е изд., стер. – М.: Издательский центр «Академия», 2010. – 384 с.:
Для заметок
