Уравнения первого порядка

Оглавление

1. Уравнения первого порядка. 4

1.1.Уравнения с разделяющимися переменными и уравнения, приводящиеся к ним 4

1.2. Геометрические и физические задачи. 5

Задание 1. 8

1.3. Однородные уравнения и уравнения, приводящиеся к ним. 10

Задание 2. 12

1.4. Линейные уравнения и уравнения Бернулли. 13

Задание 3. 15

1.5. Уравнения в полных дифференциалах. Интегрирующий множитель. 16

Задание 4. 19

1.6. Уравнения, не разрешенные относительно производной. Особые решения. 20

Задание 5. 23

1.7. Существование и единственность решения задачи Коши. 23

Метод последовательных приближений. 23

Задание 6. 25

2. Дифференциальные уравнения n-го порядка. 27

2.1. Методы интегрирования некоторых классов дифференциальных уравнений, допускающих понижение порядка. 27

Задание 7. 31

2.2. Линейные уравнения с постоянными коэффициентами. 32

Задание 8. 35

Задание 9. 36

Задание 10. 36

Задание 11. 51

3. Линейные системы с постоянными коэффициентами. 54

3.1 Матричная экспонента. 57

3.2. Формула Коши. 61

Задание 12. 61

Задание 13. 51

Задание 14. 61

Библиографический список. 51

Уравнения первого порядка

Уравнение вида

(1.1)

(уравнение, неразрешенное относительно производной), или уравнение вида

(1.2)

(уравнение, разрешенное относительно производной), связывающее независимую переменную 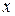, искомую функцию 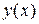и ее производную, называется дифференциальным уравнением первого порядка.

Задача отыскания решения уравнения (1.1) или (1.2), удовлетворяющего условию

, (1.3)

называется задачей Коши. Условие (1.3) – начальное условие.

Общим решением уравнения (1.1) или (1.2) называется функция такая, что

1) при любом значении постоянной 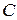эта функция является решение уравнения;

2) по начальным условиям (3) можно указать значение постоянной так, что

Соотношение вида 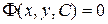, определяющее общее решение как неявную функцию, называется общим интегралом дифференциального уравнения.

Решение, получающееся из общего, при конкретном значении произвольной постоянной – частное решение.

1.1.Уравнения с разделяющимися переменными и уравнения,
приводящиеся к ним

Пусть правая часть уравнения (1.2) может быть представлена в виде произведения двух функций, каждая из которых зависит только от одной переменной: , или пусть уравнение (1.1) имеет вид . Тогда переменные в этих уравнения могут быть разделены, и мы получим следующие уравнения с разделенными переменными:

Общие интегралы этих уравнений имеют вид:

Замечание. При делении обеих частей уравнения на могли быть потеряны решения, являющиеся нулями этих функций.

Пример 1. Решить уравнение

Решение. После разделения переменных получим

. (1.4)

Интегрируя обе части полученного равенства, будем иметь

Здесь – произвольное число. Таким образом, – произвольная постоянная. Потенцируя, можем записать

Найден общий интеграл уравнения.

При разделении переменных могли быть потеряны решения, обращающие в ноль знаменатели дробей в (1.4): Непосредственная подстановка в исходное уравнение показывает, что эти функции являются его решениями. Причем решения вида могут быть получены из общего решения при , а решение должно быть добавлено к общему.

Уравнения вида сводятся к уравнению с разделяющимися переменными заменой .

Пример 2. Найти общее решение уравнения

Решение.Выполним замену . Уравнение примет вид Итак, общий интеграл уравнения имеет вид