Дифференциальные уравнения первого порядка

Дифференциальные уравнения с разделёнными переменными:

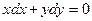
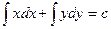
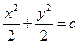
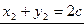
Простейшие дифференциальные уравнения с разделяющимися переменными:

Общий вид:

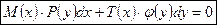(разделим на 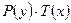, т. е. делим на то, что мешает проинтегрировать уравнение)

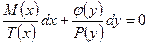и далее проинтегрируем, как с разделёнными переменными.

Например:

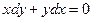
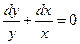
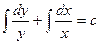
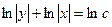
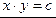(т. к. сумма логарифмов есть логарифм произведения)

Линейные дифференциальные уравнения

Общий вид:

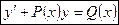. Решаются такие уравнения:

,

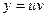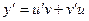
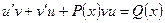
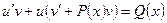
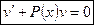
Из этого уравнения выражаем V, подставляем в предыдущее уравнение, находим U.

Ответ записываем так: 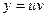. Например:

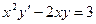
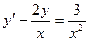
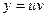
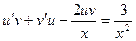
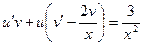
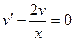
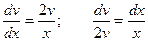
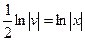
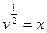
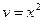
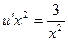
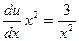
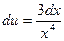
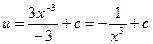
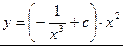
Однородные дифференциальные уравнения

Общий вид:

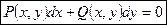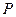, где и 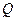— однородные функции

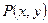— однородная, если .

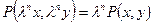Решаются такие уравнения заменой 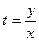. Например:

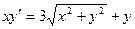
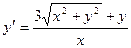
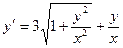
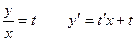
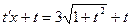
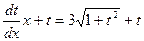(умножим на )

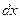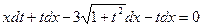(разделим на )

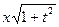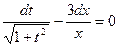. После интегрирования получим:

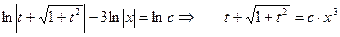
Ответ: .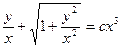

Дифференциальные уравнения второго порядка

Уравнение, содержащее производные или дифференциалы второго порядка, называются дифференциальными уравнениями второго порядка:

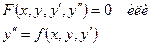
Общим решением уравнения 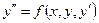называется функция 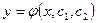, содержащая две произвольные постоянные 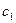и 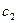и удовлетворяющая условиям:

1. при любых значениях постоянных 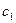и 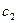функция 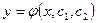является решением дифференциального уравнения;

2. каковы бы не были начальные условия 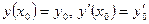, существуют единственные значения 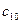и 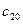такие, что функция 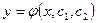является решением дифференциального уравнения и удовлетворяет начальным условиям.

Частным решением дифференциального уравнения второго порядка уравнения называется всякое решение 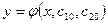, получающееся из общего решения 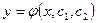при фиксированных значениях 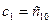и .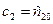

Простейшие уравнения второго порядка имеют вид:

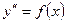или 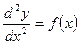. Уравнение такого вида решается двукратным интегрированием.

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами (ЛОДУ)

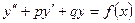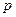ЛДУ второго порядка называются уравнения вида , где и 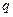— постоянные величины, а 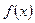— непрерывная функция.

Уравнения вида 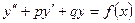называются ещё неоднородными дифференциальными уравнениями второго порядка.

Если 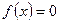, то уравнение 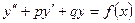принимает вил:

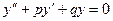— ЛОДУ второго порядка с постоянными коэффициентам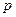и и .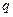

Теорема 1

Если 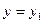— решение уравнения 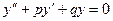, то и 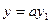, где — постоянный множитель, также будет решением данного уравнения.

Теорема 2

Если 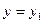, 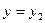— решение уравнения 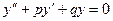, то и сумма 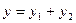также будет решением данного уравнения.

Два частных решения уравнения называются линейно зависимыми, если одно из них может быть получено умножением другого на какой-либо постоянный множитель, в противном случае частное решение называют линейно независимыми.

Теорема 3

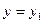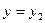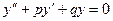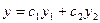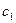Если и — линейно независимые частные решения уравнения , то общее решение его будет , где и 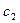— произвольные постоянные величины.

Частными линейно-независимыми решениями уравнения 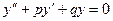являются функции вида: 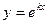, где k — произвольное число, которое нужно найти.