Властивості множення матриць

1. Множення матриць у загальному випадку некомутативне, тобто .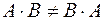

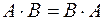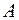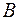Якщо ж , то кажуть, що матриці і комутують.

Одинична і нульова матриці комутують з будь-якою квадратною матрицею:

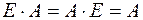
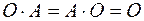
2. Нехай 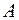, , 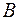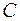- матриці такі, що визначений добуток 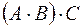, тоді визначений добуток 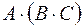і має місце рівність

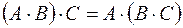( асоціативність множення матриць)

3. Нехай 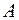, , 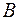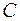– матриці такі, що визначений добуток 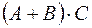, тоді визначено 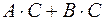і має місце рівність

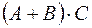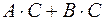= ( дистрибутивність справа множення матриць

відносно додавання ).

Якщо визначений добуток 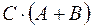, тоді визначено 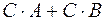і має місце рівність:

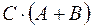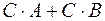= (дистрибутивність зліва множення матриць відносно додавання).

4. Якщо добуток матриць А і В визначений, то для будь-якого числа :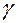

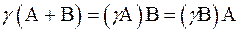(зв’язок множення матриць з множенням матриць на число).

Ранг матриці

Визначення. Мінором 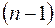-го порядку або мінором елемента 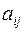матриці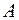 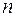-го порядку називається визначник матриці 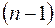-го порядку, яка утворена з матриці 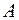викреслюванням 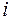-го рядка і 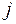-го стовпця. Позначається .

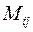Означення. Алгебраїчним доповненням елемента 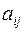матриці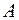 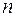-го порядку називається його мінор, взятий із знаком 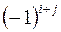. Позначається .

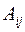За означенням

= .

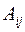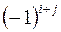
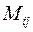Визначення. Рангом матриці 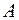розмірності 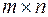називається найвищий порядок відмінних від 0 мінорів, утворених з елементів матриці 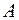. Позначається

r(A), r . Зрозуміло, що .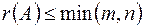

Ранг матриці можна знаходити методом обвідних мінорів або методом елементарних перетворень.

2.1) Метод обвідних мінорів застосовується таким чином: нехай в матриці А знайдено мінор к-того порядку М, відмінний від 0. Розглянемо тільки ті мінори (к+1) порядку, які містять у собі (обводять) мінор М. Якщо всі вони дорівнюють 0, то ранг матриці дорівнює к. В протилежному випадку серед обвідних мінорів знайдеться ненульовий мінор (к+1) порядку, і вся процедура повторюється.

2.2) На практиці для знаходження рангу зручно користуватися елементарними перетвореннями матриці,за допомогою яких матрицю перетворюють в ступінчасту матрицю, ранг якої установлюється за її зовнішнім виглядом: зводять до матриці, у якої нижче головної діагоналі усі елементи – нулі. Тоді ранг матриці дорівнює кількості елементів головної діагоналі, відмінних від нуля.

Визначення. Елементарними перетвореннями матриці називаються такі перетворення:

1) переставлення двох рядків (стовпців);

2) множення рядка (стовпця) на довільне дійсне число, відмінне від 0 ;

3) додавання до одного рядка (стовпця) іншого рядка (стовпця) помноженого на довільне дійсне число;

4) викреслювання або дописування нульового рядка (стовпця).

Теорема. Елементарні перетворення не змінюють рангу матриці.

Визначення. Дві матриці називаються еквівалентними, якщо одна отримана з другої за допомогою ланцюжка елементарних перетворень над рядками (стовпцями). Позначається ~ .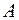

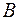Приклад. Обчислити ранг матриці за допомогою елементарних перетворень:

~ ~

~

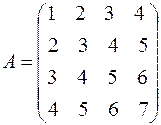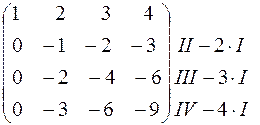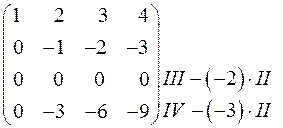
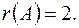
Остання матриця – ступінчаста. Її ранг дорівнює кількості ненульових рядків.

3. Оберненість матриць. Обчислення оберненої матриці.

Визначення. Матрицею, оберненою до матриці 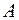, називається матриця, що позначається 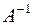, для якої виконуються рівності:

.

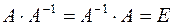Матриця, для якої існує обернена матриця, називається оборотною .

Не всяка матриця має обернену. В алгебрі матриць доведено, що матриця А має обернену при виконанні двох умов:

1) матриця А квадратна;

2) визначник матриці А не дорівнює нулю.

Зауваження. Квадратна матриця, у якої визначник не дорівнює нулю, називається не виродженою.

Теорема (про оберненість матриць). Для кожної невиродженої квадратної матриці існує єдина обернена матриця. Якщо квадратна матриця вироджена, то для неї оберненої матриці не існує.

Обернену матрицю до матриці А можна знаходити двома способами:

3.1) за допомогою формули

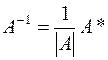, де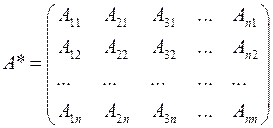

яка отримана з матриці 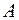заміною кожного елемента його алгебраїчним доповненням з подальшим транспонуванням. Матриця 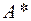називається приєднаною для матриці .

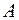Приклад. Знайти 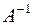, якщо .

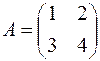Розв’язування: ;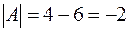

; ;

; ;

.

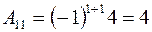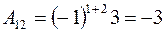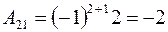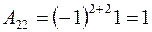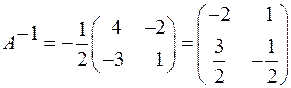Перевірка: 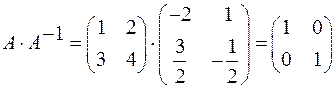.