Дифференцируемость ф.н.п
Будем, простоты ради, снова ограничиваться случаем функции 2-х переменных z= f(x, y), определённой в области Д. Пусть М0(x0, y0) некоторая точка в Д. Давая x и y некоторые приращения  и
и  в точке М0, вычислим соответствующее полное приращение функции в этой точке:
в точке М0, вычислим соответствующее полное приращение функции в этой точке: 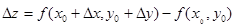 . В случае функции одной переменной y= f(x), мы называли её дифференцируемой в точке, если в точке она имела производную
. В случае функции одной переменной y= f(x), мы называли её дифференцируемой в точке, если в точке она имела производную 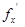 . Для ф.н.п. это определение не годится. Дадим другое определение.
. Для ф.н.п. это определение не годится. Дадим другое определение.
Определение 1: функция двух переменных z= f(x, y) называется дифференцируемой в точке (x0, y0), если её полное приращение в этой точке может быть представлено в виде 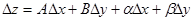 (1), где А и В постоянные, не зависящие от
(1), где А и В постоянные, не зависящие от  и
и  , а величины
, а величины 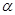 и
и 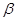 зависят от
зависят от  и
и  и стремятся к нулю, когда
и стремятся к нулю, когда  и
и  .
.
По аналогии со случаем одной переменной будем называть функцию 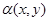 , б. м. в. в точке (x0, y0), если
, б. м. в. в точке (x0, y0), если 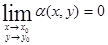 , и введём в рассмотрение б. м. величину
, и введём в рассмотрение б. м. величину 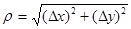 . Она стремится к нулю при
. Она стремится к нулю при  и
и  .Сумма первых двух слагаемых
.Сумма первых двух слагаемых 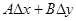 линейно зависит от
линейно зависит от  и
и  . Сумма двух последних слагаемых
. Сумма двух последних слагаемых 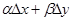 уже не линейно зависит от
уже не линейно зависит от  и
и  и есть б.м. величина высшего порядка малости по сравнению с б. м. в.
и есть б.м. величина высшего порядка малости по сравнению с б. м. в.
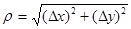 , в самом деле:
, в самом деле: 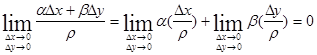 т.е.
т.е. 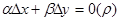 . Таким образом, сумма первых двух слагаемых
. Таким образом, сумма первых двух слагаемых 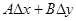 линейно зависит от
линейно зависит от  и
и  и отличается от
и отличается от  на б. м. в. высшего порядка малости по сравнению с
на б. м. в. высшего порядка малости по сравнению с 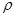 :
: 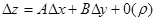 . Линейная часть называется поэтому главной частью полного приращения.
. Линейная часть называется поэтому главной частью полного приращения.
Определение 2: Если функция z= f(x, y) дифференцируема в точке (x0, y0), то линейная относительно  и
и  часть её полного приращения называется полным дифференциалом функции в этой точке:
часть её полного приращения называется полным дифференциалом функции в этой точке: 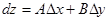 (2).
(2).
Из определения 1 дифференцируемой функции легко установить следующие факты:
1.Если функция дифференцируема в точке, то она имеет в этой точке и частные производные 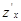 и
и 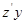 .
.
 В самом деле, если функция z= f(x, y) дифференцируема в точке (x0, y0), то в ней имеет место формула (1). Положим
В самом деле, если функция z= f(x, y) дифференцируема в точке (x0, y0), то в ней имеет место формула (1). Положим 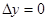 . Тогда
. Тогда 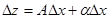 .
. 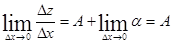 или
или 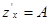 . Совершенно аналогично, полагая
. Совершенно аналогично, полагая 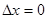 , получим
, получим 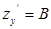 т.е существует. Кстати, отсюда следует, что полное приращение дифференцируемой функции может быть записано в виде
т.е существует. Кстати, отсюда следует, что полное приращение дифференцируемой функции может быть записано в виде 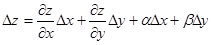 (
( 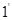 ), а полный дифференциал
), а полный дифференциал 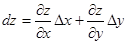 или
или 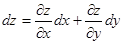
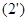 или
или 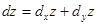 , т.е. полный дифференциал есть сумма частных дифференциалов.
, т.е. полный дифференциал есть сумма частных дифференциалов.
В формулах (1’) и (2’) частные производные вычисляются в точке (x0, y0), где функция дифференцируема.
 Заметим, что т.к.
Заметим, что т.к. 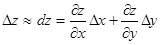 , то полный дифференциал широко применяется в приближённых вычислениях: ибо
, то полный дифференциал широко применяется в приближённых вычислениях: ибо 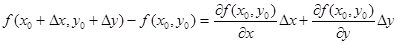 , откуда
, откуда 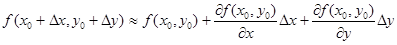
2). Из формулы (1) легко показать, что если функция дифференцируема в точке (x0, y0),то она и непрерывна в этой точке.
В самом деле: 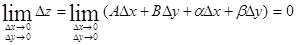 , что и означает непрерывность функции в точке (x0, y0).
, что и означает непрерывность функции в точке (x0, y0).
Показано, что, если функция дифференцируема, то она имеет и частные производные 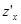 и
и 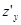 . Обратное утверждение, вообще говоря, неверно. Из существования частных производных дифференцируемость ещё не следует. Нужны дополнительные условия. Приведём наиболее простое и употребительное достаточное условие дифференцируемости.
. Обратное утверждение, вообще говоря, неверно. Из существования частных производных дифференцируемость ещё не следует. Нужны дополнительные условия. Приведём наиболее простое и употребительное достаточное условие дифференцируемости.
Теорема: если функция z= f(x, y) имеет частные производные 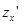 и
и 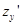 как в самой точке (x0, y0) так и в некоторой её окрестности и они в самой точке непрерывны, то функция дифференцируема в точке (x0, y0).
как в самой точке (x0, y0) так и в некоторой её окрестности и они в самой точке непрерывны, то функция дифференцируема в точке (x0, y0).
Доказательство: пусть в некоторой  - окрестности точки (x0, y0) существуют частные производные
- окрестности точки (x0, y0) существуют частные производные 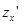 и
и 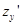 , непрерывные в самой точке. Рассмотрим полное приращение
, непрерывные в самой точке. Рассмотрим полное приращение  функции в точке (x0, y0) и покажем, что оно может быть записано в виде (1) или (1’) при всех условиях.
функции в точке (x0, y0) и покажем, что оно может быть записано в виде (1) или (1’) при всех условиях. 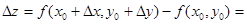
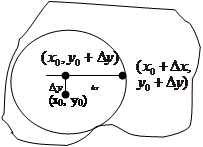
Разность 1 можно рассматривать как приращение функции в точке 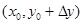 , вызванное приращением аргумента x:
, вызванное приращением аргумента x:  , а саму функцию в этом случае как функцию одного независимого переменного x:
, а саму функцию в этом случае как функцию одного независимого переменного x: 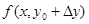 .Производная функции
.Производная функции 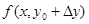 совпадает с частной производной
совпадает с частной производной 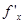 , которая существует в
, которая существует в 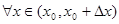 . Но раз производная существует, то сама функция непрерывна, и потому к ней применима теорема Лангранжа:
. Но раз производная существует, то сама функция непрерывна, и потому к ней применима теорема Лангранжа:
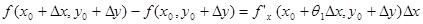 , где
, где 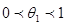 (3).
(3).
Совершенно аналогично разность 2 можно рассматривать как частное приращение функции по y и по теореме Лангранжа записать, что 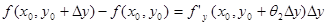 , где
, где 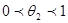 (4).
(4).
Из (3) и (4) имеем: 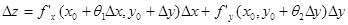 (5)
(5)
Обозначим: 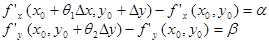 (6)
(6)
Из (5) и (6) получаем, что 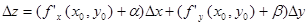 или
или 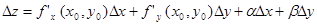 (7). Из (6) видно, что
(7). Из (6) видно, что 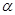 и
и 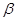 зависят от
зависят от  и
и  . Покажем, что
. Покажем, что 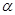 и
и 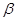
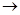 0 при
0 при  и
и 
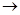 0. Прежде всего,
0. Прежде всего, 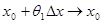 и
и 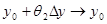 при
при 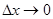 и
и 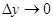 . А так как по условию
. А так как по условию 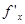 и
и 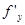 непрерывны в точке (x0, y0), то разности слева в (6),а значит, и величины
непрерывны в точке (x0, y0), то разности слева в (6),а значит, и величины 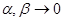 . Тем самым всё доказано, т.к. полное приращение
. Тем самым всё доказано, т.к. полное приращение  действительно представлено в виде (1’) с выполнением требований определения 1. Значит, функция дифференцируема в точке (x0, y0).
действительно представлено в виде (1’) с выполнением требований определения 1. Значит, функция дифференцируема в точке (x0, y0).
Эта теорема даёт условия достаточные, но они не являются необходимыми, так как уже для функции одной переменной (а она может рассматриваться как частный случай функции любого числа переменных) непрерывность производной необязательна.
Из теоремы следует, что если частные производные существуют и непрерывны в некоторойокрестности точки, то, тем более, функция дифференцируема в этой точке.
В дальнейшем рассматриваем чаще всего именно такой случай.
Замечание: функция 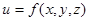 называется дифференцируемой, если
называется дифференцируемой, если 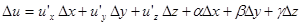 , причём,
, причём, 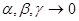 при
при 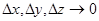 , т.е. аналогичное определение.
, т.е. аналогичное определение.
§5 Производные сложных функций нескольких переменных. Полная производная.
Как и в случае одной переменной, в случае ф.н.п. рассматриваются сложные функции (функции от функций). При этом как сами функции, так и их промежточные аргументы могут быть от любого числа.
1) Пусть дана функция 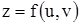 и аргументы u и v сами есть функции от независимой переменной
и аргументы u и v сами есть функции от независимой переменной 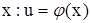
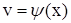 . Тогда
. Тогда 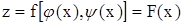 , т.е. сложная функция от x.
, т.е. сложная функция от x.
Предположим, что функции 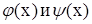 имеют производные по x в точке
имеют производные по x в точке 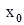 , а функция
, а функция 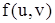 имеет непрерывные частные производные в окрестности соответствующей точки (u, v). Выразим тогда производную
имеет непрерывные частные производные в окрестности соответствующей точки (u, v). Выразим тогда производную 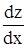 через частные производные
через частные производные 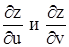 и производные функций u и v по x.
и производные функций u и v по x.
Дадим аргументу x приращение 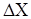 , тогда функции u и v получат соответствующие приращения
, тогда функции u и v получат соответствующие приращения 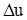 и
и 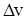 , а функция z - приращение
, а функция z - приращение  .
.
Так как 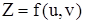 дифференцируема (она имеет непрерывные частные производные
дифференцируема (она имеет непрерывные частные производные 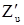 и
и 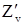 ), то
), то 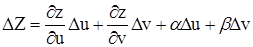 , причём
, причём 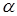 и
и 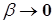 при
при 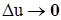 и
и 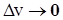 .
.
Разделим неравенство почленно на 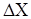 :
:
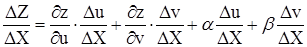 .
.
Перейдём к пределу при 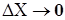 . Тогда
. Тогда 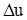 и
и 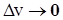 тоже, ибо функции u и v имеют производные в точке Х, а потому непрерывны в ней. Но тогда и
тоже, ибо функции u и v имеют производные в точке Х, а потому непрерывны в ней. Но тогда и 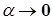 и
и 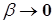 . Получим
. Получим
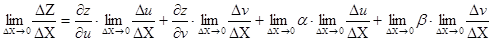
Оттуда 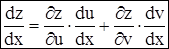 (1) или
(1) или 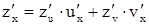 .
.
В частности, если 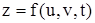 и
и 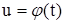
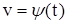 , то z зависит от t и непосредственно и через посредство u и v. Тогда:
, то z зависит от t и непосредственно и через посредство u и v. Тогда:
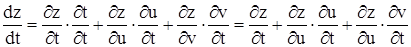 . (1’)
. (1’)
Эту производную называют полной производной функции z по аргументу t ( в отличие от частной производной 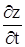 , которая является лишь одним из слагаемых для полной производной
, которая является лишь одним из слагаемых для полной производной 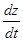 ).
).
2) Пусть теперь 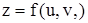 и
и 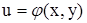 ,
, 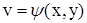 , т.е. промежуточные аргументы сами есть функции от двух переменных x и y.
, т.е. промежуточные аргументы сами есть функции от двух переменных x и y.
Тогда 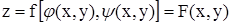 , т.е. сложная функция от двух аргументов x и y. Можем говорить о частных производных
, т.е. сложная функция от двух аргументов x и y. Можем говорить о частных производных 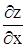 и
и 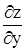 . Выразим их через частные производные по промежуточным аргументам функции z и промежуточных аргументов по х и у. Предположим, что существуют непрерывные частные производные по всем аргументам у функций
. Выразим их через частные производные по промежуточным аргументам функции z и промежуточных аргументов по х и у. Предположим, что существуют непрерывные частные производные по всем аргументам у функций 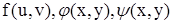 . Тогда оказываются справедливы формулы:
. Тогда оказываются справедливы формулы: 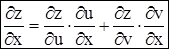 (2) и
(2) и 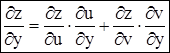 (3).
(3).
В самом деле, предположим, что y зафиксировано, тогда z есть сложная функция только от x. Находимся в условиях 1) случая. (1) запишется в виде формулы (2).
Аналогично, считая фиксированным x, получим формулу (3).
Пример: 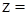 u2
u2 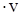 , u = sin(x2+y), v = cos(x+y2). Найти
, u = sin(x2+y), v = cos(x+y2). Найти 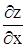
 .
.
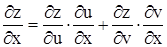 = 2uv
= 2uv 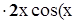 2 +y) – u2 sin (x+y2 )=
2 +y) – u2 sin (x+y2 )=
=4x sin(x2+y ) 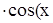 +y2)
+y2) 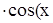 2+y) – sin2(x2+y )
2+y) – sin2(x2+y ) 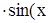 +y2)
+y2)
