Ряды Маклорена и Тейлора
Рассмотрим произвольную функцию f (x), определенную в заданном интервале | x - x0 | < R, и предположим для нее, что в точке x0 существуют производные всех порядков до n-го включительно. Будем искать многочлен n-степени с неизвестными пока коэффициентами, который наилучшим образом приближается к функции f (x):
Pn(x) = a0 + a1( x - x0 ) + a2 ( x - x0 )2 + ¼ + an ( x - x0 )n » f (x). (20)
Для этого потребуем, чтобы функция f (x) и ее n производных были равны значению многочлена Pn(x) и его производных в точке x0. Если x0 = 0, то
Pn(x) = a0 + a1 x + a2 x2 + ¼ + an xn » f (x). (21)
Как видно из (21)
Pn(0) = a0 = f (0).
Для нахождения коэффициентов ai ( i = 1, 2, ¼, n) продифференци-руем (21) почленно:
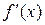 = a1 + 2 a2 x + 3 a3 x2 + 4 a4 x3 + ¼ + n an xn-1 +¼,
= a1 + 2 a2 x + 3 a3 x2 + 4 a4 x3 + ¼ + n an xn-1 +¼,
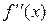 = 2 a2 + 2×3 a3 x + 3×4 a4 x2 + ¼ + n×(n-1) an xn-2 +¼, (22)
= 2 a2 + 2×3 a3 x + 3×4 a4 x2 + ¼ + n×(n-1) an xn-2 +¼, (22)
……………………………………………………………
Как видно из (22) при x = 0: f¢(0) = a1, f¢¢(0) = 2 a2, f¢¢¢(0) = 2×3 a3,
f (4)(0) = 2×3×4 a4 , ¼, f (n)(0) = 2×3×4×¼×n an. Отсюда для коэффициентов многочлена (21) получим:
a0 = f (0), a1 = f¢ (0), a2 = 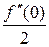 , a3 =
, a3 = 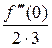 , a4 =
, a4 = 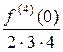 , ¼, an =
, ¼, an = 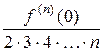 .
.
Приближение функции f (x) многочленом (21) примет вид (n! = 1×2×3×4×¼×n):
f (x) » f (0) + 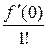 x +
x + 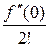 x2 +
x2 + 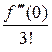 x3 + ¼ +
x3 + ¼ + 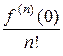 xn. (23)
xn. (23)
В тех случаях, когда функция f (x) или ее производные теряют смысл при x = 0, пользуются более общим представлением (20) функции в виде многочлена. Легко показать, что для приближения функции f (x) многочленом (20) справедливо выражение:
f (x) » f (x0)+ 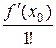 (x-x0)+
(x-x0)+ 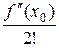 (x-x0)2 +
(x-x0)2 + 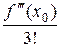 (x-x0)3 + ¼
(x-x0)3 + ¼
¼+ 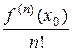 (x-x0)n. (24)
(x-x0)n. (24)
Многочлены (23) и (24) дают лишь некоторое приближение для функции f (x). В связи с этим возникает вопрос о степени близости f (x) и соответствующего многочлена. Разность
f (x) - Pn(x) = rn(x) (25)
называется остаточным членом. Так как n мы можем брать сколь угодно большим, то выражения (23) и (24) приводят к разложению f(x) в бесконечный степенной ряд
f (x) = f (x0) + 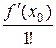 (x - x0) +
(x - x0) + 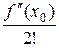 (x - x0)2 +
(x - x0)2 + 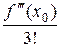 (x - x0)3 + ¼
(x - x0)3 + ¼
¼ + 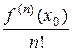 (x - x0)n + ¼ (26)
(x - x0)n + ¼ (26)
при | x - x0 | < R.
Впервые возможность представления функции в виде бесконечного ряда была доказана Тейлором. При x0 = 0 такой ряд был выведен Маклореном:
f (x) = f (0) + 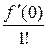 x +
x + 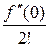 x2 +
x2 + 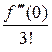 x3 + ¼ +
x3 + ¼ + 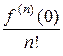 xn + ¼. (26¢)
xn + ¼. (26¢)
Разность между f (x) и суммой (n+1) членов ряда, согласно (25), есть как раз остаточный член rn (x). Тогда очевидно, что для того, чтобы при некотором значении x действительно имело место разложение (26), необходимо и достаточно, чтобы
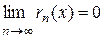 . (27)
. (27)
Замечание.Для непрерывной вместе со своими производными функции f (x), как правило, условие (27) выполняется и функция f (x) разлагается в степенной ряд. Далее приведены примеры разложения элементарных функций в степенные ряды.
Пример 10. Разложить в ряд функцию f (x) = ex. Все производные функции ex равны ex. Полагая x = 0, получим f (0) = = 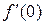 =
= 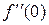 = ¼ = 1. Подставляя эти значения в ряд (26¢), будем иметь разложение функции
= ¼ = 1. Подставляя эти значения в ряд (26¢), будем иметь разложение функции 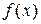 = ex в ряд Маклорена:
= ex в ряд Маклорена:
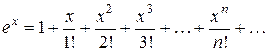 (28)
(28)
Применяя к этому ряду признак Даламбера
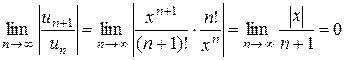 .
.
Степенной ряд (28) сходится для любого x; интервал сходимости - (-¥, ¥).
Пример 11. Разложить в ряд функцию f (x) = 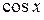 .
.
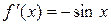 ,
, 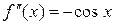 ,
, 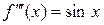 ,
, 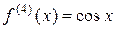 , ¼
, ¼
При x = 0
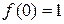 ,
, 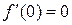 ,
, 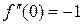 ,
, 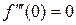 ,
, 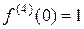 , ¼
, ¼
Подставляя в (26¢), получим
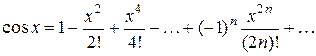 , (29)
, (29)
где x измеряется в радианах.
Пример 12. Разложить в ряд функцию f (x) = 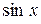 .
.
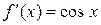 ,
, 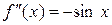 ,
, 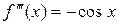 ,
, 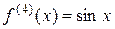 , ¼
, ¼
При x = 0
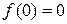 ,
, 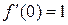 ,
, 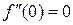 ,
, 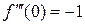 ,
, 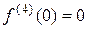 , ¼
, ¼
Подставляя в (26¢), получим
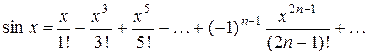 (30)
(30)
Разложение (30), также как и (29), справедливо при любом x.
Пример 13. Разложить в ряд функцию f (x) = 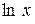 . Функция
. Функция 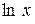 не определена при x = 0, поэтому разложим ее в ряд Тейлора (26) по возрастающим степеням (x-1) (при x0 = 1).
не определена при x = 0, поэтому разложим ее в ряд Тейлора (26) по возрастающим степеням (x-1) (при x0 = 1).
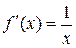 ,
, 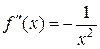 ,
, 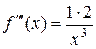 ,
, 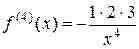 , ¼
, ¼
При x = 1
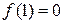 ,
, 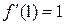 ,
, 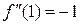 ,
, 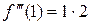 ,
, 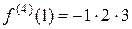 , ¼
, ¼
Подставляя в (26), находим
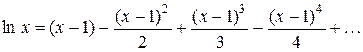
Пример 14. Разложить в ряд функцию мнимого аргумента f (x) = 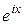 . Обозначим z = ix. Зная разложение в ряд функции ex, запишем
. Обозначим z = ix. Зная разложение в ряд функции ex, запишем
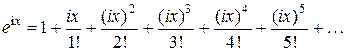
Разделяя действительную и мнимую часть, получим
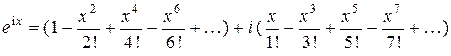 . (31)
. (31)
Согласно (29) и (30), равенство (31) можно записать в виде
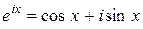 . (32)
. (32)
Заменяя x на -x и учитывая, что 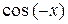 =
= 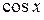 , а
, а 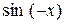 = -
= - 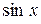 , находим
, находим
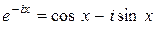 . (33)
. (33)
Формулы (32) и (33) были выведены Эйлером; разрешая (32) и (33) относительно 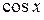 и
и 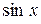 , получим
, получим
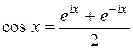 ,
, 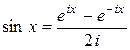 .
.
