Скалярное произведение
МАТЕМАТИКА
Методические указания
И контрольные задания для студентов заочной
Формы обучения по сокращенным образовательным
программам
Специальность 220201 – управление и информатика в технических системах
Факультет электроэнергетический
Вологда
УДК 51:378.147 (075,5)
Математика: Методические указания и контрольные задания для студентов заочной формы обучения по сокращенным образовательным программам-Вологда: ВоГТУ, 2010.- 47 с.
Данные методические указания включают в себя две контрольные работы: по линейной алгебре и математическому анализу. Каждая работа состоит из четырех заданий по 30 вариантов каждое. Методические указания прелагаются для студентов-заочников специальности 220201 электроэнергетического факультета.
Утверждено редакционно-издательским советом ВоГТУ
Составитель: Абильдин А.А., канд.техн.наук, доцент
Рецензент: Быстроумов В.А., канд.техн.наук, доцент
ВВЕДЕНИЕ
Настоящие методические указания предназначены для самостоятельного изучения основ некоторых разделов курса «Высшая математика» студентами заочного обучения специальности 220201 «управление и информатика в технических системах» В них даны указания теоретические сведения , разобраны типовые примеры. Студент не должен ограничиваться рассмотрением только этих примеров, а может закрепить свои знания, решая примеры из соответствующих разделов сборников задач по линейной алгебре и математическому анализу. Указана литература, приведены задания для контрольных работ №1 и №2
.
ТЕМА 1. ВЕКТОРЫ. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ.
Вектором называется направленный отрезок 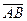 .Точка A называется началом вектора, точка B – концoм вектора.Векторы обозначают так же строчными буквами
.Точка A называется началом вектора, точка B – концoм вектора.Векторы обозначают так же строчными буквами 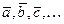 и пишут ā=
и пишут ā= 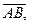
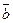 =
= 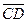
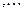 . Длину вектора
. Длину вектора 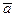 обозначаем через
обозначаем через 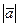 .Векторы
.Векторы 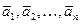 называются коллинеарными между собою,если все они,будучи приложенными в одной и той же точке, оказываются лежащими на одной прямой.
называются коллинеарными между собою,если все они,будучи приложенными в одной и той же точке, оказываются лежащими на одной прямой.
§1.1. Действия над векторами.
1.Сложение векторов.
Пусть даны векторы 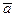 и
и 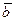 . Прилагаем вектор
. Прилагаем вектор 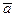 к какой-нибудь точке A,получаем
к какой-нибудь точке A,получаем 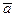 =
= 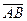 ; прилагаем
; прилагаем 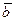 к точке B, получаем
к точке B, получаем 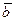 =
= 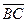 . По определению вектор
. По определению вектор 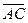 =
= 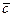 называется суммой векторов
называется суммой векторов 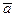 и
и 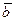 , т.е.
, т.е.
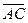 =
= 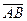 +
+ 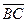

 B
B


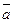
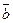
 A C
A C
рис.1
2.Умножение вектора на число.
Если отношение вектора CD к вектору AB равно числу 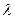 , то пишут
, то пишут 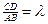 или CD=
или CD= 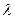 AB. Поэтому нахождение вектора CD, отношение которого к данному вектору AB равно данному числу
AB. Поэтому нахождение вектора CD, отношение которого к данному вектору AB равно данному числу 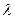 , называется умножением вектора на это число
, называется умножением вектора на это число 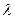 .
.
Замечание.
Линейной комбинацией векторов 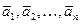 с коэффициентами
с коэффициентами 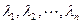 называется вектор вида
называется вектор вида 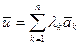 .
.
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
Определение.Скалярным произведением двух векторов 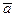 и
и 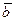 называется число (
называется число ( 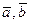 ), равное произведению длин этих векторов на косинус угла между ними
), равное произведению длин этих векторов на косинус угла между ними
( 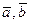 )=
)= 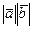 cos
cos 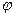 .
.
Следствие. Если два вектора 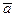 и
и 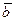 заданы своими декартовыми прямоугольными координатами,то скалярное произведение этих векторов равно сумме попарных произведений соответствующих координат, т.е.
заданы своими декартовыми прямоугольными координатами,то скалярное произведение этих векторов равно сумме попарных произведений соответствующих координат, т.е. 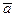 (
( 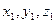 ),
), 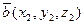
и 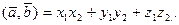
Свойства скалярного произведения.
a).( 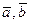 )=(
)=( 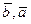 )
)
b).( 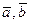 )=0 тогда и только тогда,когда векторы
)=0 тогда и только тогда,когда векторы 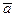 и
и 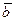 перпендикулярны между собою.
перпендикулярны между собою.
c).( 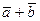 ,
, 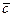 )=(
)=( 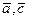 )+(
)+( 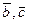 )
)
d).( 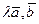 )=
)= 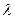 (
( 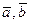 )-численный множитель можно выносить за знак скалярного произведения.
)-численный множитель можно выносить за знак скалярного произведения.
