Функции нескольких переменных. Основные определения

Если в кажд.паре чисел x,y с D на плоскости, поставлено в соответствии некот.число zcG по некот. правилу, то говорят, что на мн-ве D задана ф-ция 2-х переменных zcF(x,y – независимые пер., z – зависимая переменная).

Предел и непрерывность функции нескольких переменных.

Пусть задана Z=f(х;у), тогда А – предел ф-ции в т.М(х₀,y₀), если для любого сколь угодно малого положит. числа E>0 сущ-т полож-е число б>0, что для всех х,у выполняется нерав-во |f(x,y)-A|<E

Z=f(х;у) непрерывна в т.(х₀,y₀), если: - она опред-на в этой т.; - имеет конеч. предел при х, стрем-ся к х₀ и у к у₀; - этот предел = знач-ю ф-ции в т.(х₀,y₀), т.е. limf(х;у)=f(х₀,y₀)

Если ф-ция непрерывна в кажд. т. мн-ва Х, то она непрерывна в этой области

Частные производные функции двух переменных.

Зафиксируем т.М(x₀,y₀) и вычислим значение z=f(x₀,y₀). Затем одну переменную х будем изменять, а у будет постоянной. Дадим значению x₀ значение ∆х. f(x₀+∆x).

Пусть 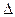х – приращение независимой переменной х в некоторой точке из области Х. Тогда величина, равная 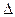z_x = f(x₀+ 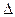х, y₀)-f(x₀,y₀) называется частным приращением в точке. Если переменную х зафиксировать, а переменной у дать приращение 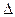у, то получим 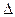z_у = f(x₀,y₀+ 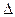у)–f(x₀,y₀)

z’_x =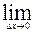

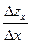
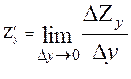
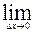
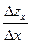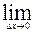
Предел отношения = 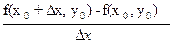, если он сущ. и конечен, назыв. частной производной по аргументу х, y=const.

Аналогично определяется ЧП по аргументу у.

Частную производную функции 2-х переменных находят по тем же правилам, что и для функций одной переменной.

Отличие состоит в том, что при дифференциации функции по переменной х , у считается const, а при дифференцировании по у, х считается const.

Изолированные const соединены с функцией операциями сложения/вычитания.

Частные производные высших порядков.

Частная производная 2-го порядка

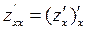
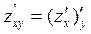
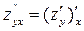
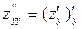
Дифференциал функции двух переменных.

z = f(x,y) явл. дифференц., если

∆z = 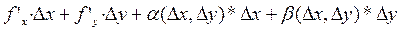(полное приращение).

Дифференциал ф-ции – .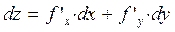

Применение дифференциалов, приближённых к вычислению.

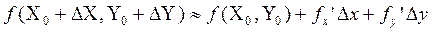
Экстремум функции двух переменных.

Точки 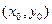называются max или min z = f(x,y), если существуют некоторые отрезки 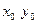такие, что для всех x и y из этой окрестности f(x,y)<f 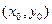или

f(x,y)>f .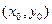

Если задана точка экстремума функции 2-х переменных, то значение частных производных в этой точке равны 0.

Точки 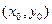, в которых частные производные первого порядка называются стационарными или критическими. Поэтому для нахождения точек экстремума функции 2-х переменных используются достаточные условия экстремума.

Пусть функция z = f(x,y) дважды дифференцируема, и 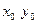стационарная точка,

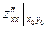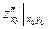A = B = C =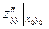

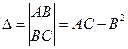, тогда

1) 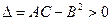, причем maxA<0, minA>0.

2) 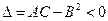экстремума нет.

3) 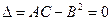он может и не может быть.