Основные операции над матрицами. Направление подготовки
КОНСПЕКТ ЛЕКЦИЙ
ПО КУРСУ МАТЕМАТИКИ
Направление подготовки
080200.62 «Менеджмент»
Квалификация (степень) выпускника
Бакалавр
Нижнекамск - 2013
Раздел I: Линейная алгебра с элементами аналитической геометрии
Тема 1 Матрицы и операции над ними
Лекция 1.1.1 «Матрицы и операции над ними»
Учебные вопросы:
1. Матрицы
2. Основные операции над матрицами
Матрицы
Статистические, производственные показатели, а также расчеты, производимые на основе полученной информации, часто требуют сохранения результатов для их дальнейшего использования. В этом случае создаются числовые таблицы, в которых информация в той или иной степени упорядочена. Экономические и финансовые расчеты, которые являются наиболее широко используемыми во всех сферах деятельности человека (от семейного бюджета до бюджета государства), также должны быть упорядочены. Одной из форм такого упорядоченного состояния любой системы является наличие множества таблиц с определенной информацией. Для оптимизации работы с такими таблицами используют матричное представление данных.
Таблицу
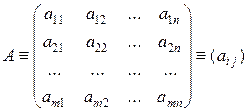
называют (прямоугольной) матрицей размера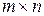 
. Элементы 
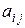называются элементами матрицы; элемент 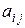расположен в 
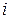-й строке и в 
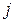-м столбце матрицы; 
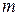есть число строк, а 
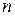–число столбцов.
Пример. Матрица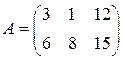 
имеет размер 
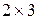, 2 строки и 3 столбца.
Матрица, состоящая из одной строки, называется матрицей (вектором)-строкой, а из одного столбца – матрицей (вектором)-столбцом.
Если в матрице число строк равняется числу столбцов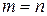 
(матрица размера 
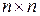), то матрицу называют квадратной матрицей порядка 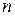. Элементы матрицы, у которых номер столбца равен номеру строки, называются диагональными и образуют главную диагональ матрицы. Другая диагональ называется побочной диагональю. Квадратная матрица 
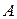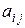=( ) называется:
симметричной относительно главной диагонали, если =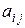 
;
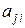диагональной, если 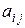=0 при 
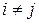(все элементы, не стоящие на главной диагонали, равны нулю);
треугольной (наддиагональной), если 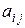=0 при 
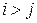(все элементы, стоящие ниже главной диагонали, равны нулю);
строго треугольной, если 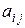=0 при 
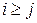(все элементы, стоящие на главной диагонали и ниже ее, равны нулю).
Пример. Матрица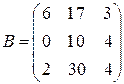 
- квадратная 3-го порядка; матрица
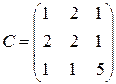- симметричная относительно главной диагонали; матрица 
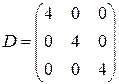- диагональная; матрица 
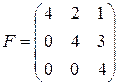- треугольная (наддиагональная); матрица 
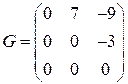- строго треугольная.
Единичной матрицей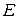 
называется диагональная матрица с единичными диагональными элементами:
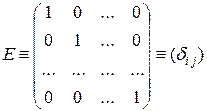, где 
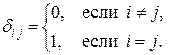
Пример. Матрица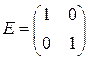 
- единичная матрица 2-го порядка.
Матрица размера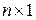 
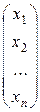
называется столбцом, а матрица размера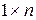 
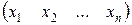
– строчкой.
Нулевой матрицей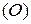 
размера 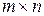называется матрица этого размера, все элементы которой равны нулю.
Пример. Матрица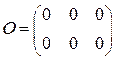 
- нулевая матрица размера .
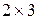Матрицей, транспонированной по отношению к матрице 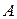=( 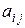) размера 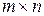, называется матрица 
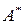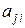=( ) размера 
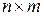(столбцы матрицы 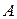являются строками матрицы 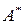с теми же номерами).
Пример. Пусть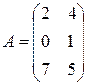 
. Транспонированной матрицей 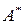будет
.
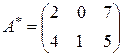Основные операции над матрицами
Две матрицы 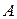=( 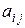) и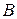 
=( 
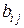) равны друг другу, если они одинакового размера и их соответствующие элементы равны, т. е.
,
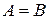если
=
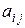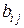
для всех 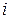и .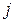
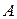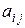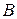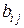Сумма двух матриц =( ) и =( ) размера 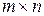есть матрица 
=( 
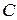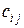) размера 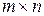, у которой элементы являются суммой соответствующих элементов матриц слагаемых, т. е.
,
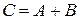если
= +
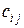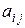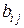
для всех 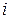и .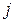
Произведение матрицы 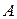=( 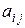) размера 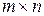на число 
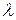есть матрица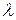 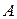размера 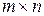, у которой элементы равны соответствующим элементам матрицы 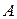, умноженным на :
= ( )=( ).
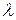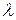
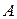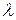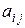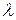
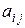Пример. Даны матрицы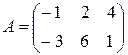 
и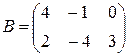 
. Найти матрицу 
.
◄ = 
= 
=
= 
= 
. ►
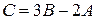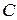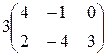
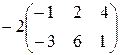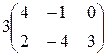
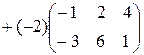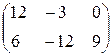
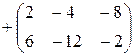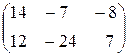Вычитание матриц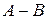 
можно выполнять либо вычитанием соответствующих элементов матриц, либо, как в приведенном примере, через прибавление противоположнойматрицы – (– 
):
= 
.
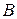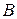
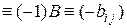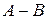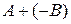Произведение матрицы 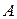=( 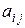) размера 
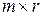на матрицу 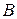=( 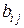)размера 
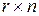есть матрица 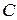=( 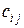) размера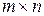
( 
)( 
) 
( ),
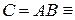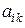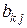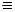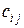где
= 
.
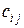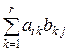Таким образом, элемент 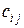матрицы 
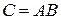есть сумма произведений элементов 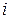-й строки матрицы 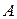на соответствующие элементы 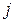-го столбца матрицы 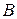. В каждом произведении матриц 
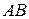форма матриц 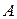и 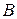должна быть согласованной: число столбцов 
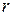матрицы 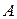должно равняться числу строк матрицы 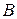. Из существования произведения 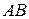вовсе не следует существование произведения 
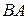.Если существуют оба произведения 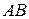и 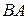(это, в частности, будет всегда, есл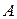и и 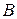– квадратные матрицы одного порядка), то, вообще говоря,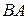 
.
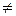
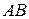Пример. Даны матрицы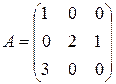 
и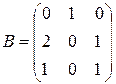 
. Найти .
◄ = 
=
= 
= 
. ►
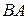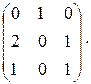
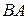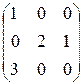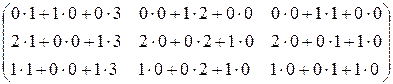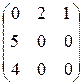Для операций над матрицами справедливы следующие соотношения
( , 
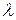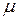– числа, 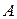, , 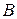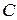– матрицы, 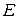– единичная матрица):
, 
,
, 
,
, 
,
, 
,
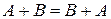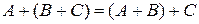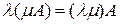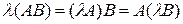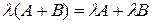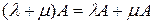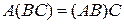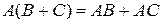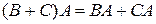
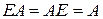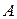( – квадратная матрица).