Вычитая левые и правые части последних соотношений, получим

Метод дихотомии

Пусть необходимо найти решения уравнений вида(1.1):

f(x)=0

т.е. необходимо найти x*, такое что f(x*)=0

Считаем, что отделение корней уравнения (1.1) проведено, это означает, что а) известен интервал [a,b], в котором находится решение уравнения; б) в этом интервале находится только один корень; в) вычислены значения функции f(x) на концах этого отрезка f(a) и f(b) и эти значения имеют разные знаки. Задача заключается в том, что необходимо определить корень уравнения с погреш­ностью e (рис. 1.2).

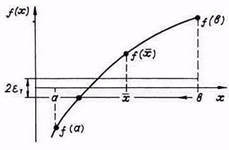
Рис. 1.2. Метод дихотомии

Метод дихотомии, или метод деления отрезка пополам, заключается в следующем. Определяем середину отрезка [а, b]:

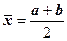
и вычисляем функцию 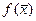. Далее делаем выбор, какую из двух частей отрезка взять для дальнейшего уточнения корня. Если левая часть уравнения f(x) есть непрерывная функция аргумента х, то корень будет находиться в той половине отрезка, на концах которой f(x) имеет разные знаки. Т.е.:

- если 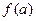и и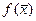меют одинаковые знаки, то а переносим в ;

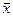- есл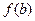и и 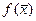имеют одинаковые знаки, то b переносим в ;

На рис. 1.2 это будет отрезок [а, ], т.е. для очередного шага уточнения точку b перемещаем в середину отрезка и продолжаем процесс деления как с первоначальным отрезком [а, b].

Итерационный (повторяющийся) процесс будем продолжать до тех пор, пока интервал [а, b] не станет меньше заданной погрешности e:

|b-a|<e

Следует учитывать, что функция f(x) вычисляется с некоторой абсолютной погрешностью e₁. Вблизи корня значения функции f(x) малы по абсолютной величине и могут оказаться сравнимыми с погрешностью ее вычисления. Другими словами, при подходе к корню мы можем попасть в полосу шумов 2e₁ и дальнейшее уточнение корня окажется невозможным. Поэтому надо задать ширину полосы шумов и прекратить итерационный процесс при попадании в нее:

|f(a)|<e₁

и

|f(b)|<e₁

Также необходимо иметь в виду, что при уменьшении интервала [а, b] увеличивается погрешность вычисления его длины b - а за счет вычитания близких чисел.

Метод дихотомии позволяет значительно уменьшить объем вычислений по сравнению с графическим методом. Так как за каждую итерацию интервал, где расположен корень, уменьшается в два раза, то через n итераций ин­тервал будет равен (b - а)/2ⁿ. За 10 итераций интервал уменьшится в 2¹⁰ = 1024 » 10 ³ раз, за 20 итераций - в 2²⁰ » 10⁶ раз. Таким образом, в методе дихотомии корень уравнения с относительной погрешностью δ=10^-6 можно определить примерно за 20 итераций.

Метод хорд

Рассматриваемый метод так же, как и метод дихотомии, предназначен для уточнения корня на интервале [а, b], на концах которого левая часть решаемого уравнения f(x) принимает разные знаки. Интервал [а, b] по-прежнему определяем графическим методом. Очередное приближение теперь в отличие от метода дихотомии берем не в середине отрезка, а в точке х₁, где прямая линия, проведенная через точки f(a) и f(b), пересекает ось абсцисс (рис. 1.3).

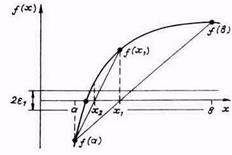
Рис. 1.3. Метод хорд

Уравнение прямой линии, проходящей через точки f(a) и f(b), запишем в общем виде

у(х) = kx + с

Коэффициенты k и с уравнения этой прямой определим из условий f(a)=ka+с, f(b)=kb+с.

Вычитая левые и правые части последних соотношений, получим

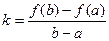
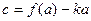
Точку пересечения прямой у(х) с осью абсцисс получим, приравнивая у(х) нулю,

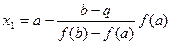(1.7)

или

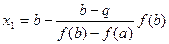(1.8)

В качестве нового интервала для продолжения итерационного процесса выбираем тот из двух [a, x₁] или [х₁, b], на концах которого функция f(x) принимает значения с разными знаками.

Заканчиваем процесс уточнения корня, когда расстояние между оче­редными приближениями станет меньше заданной погрешности e:

|x_n-x_n-1|<e

или когда значения функции f(x) попадут в область шума, т.е.

|f(x_n)|<e₁