Методические указания. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1
По дисциплине: ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ
Наименование работы: ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ. ДЕЙСТВИЯ НАД МАТРИЦАМИ.
Для специальности 230111, 230115.
Составлено преподавателем Калмыковой О.И.
г. Смоленск
2012 г.
Практическое задание №1
По дисциплине: ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ (2 курс)
Наименование работы: ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ. ДЕЙСТВИЯ НАД МАТРИЦАМИ.
1. Цель работы:Приобретение навыков работы с определениями второго и третьего порядка, их вычисление. Научиться находить транспонированную, обратную матрицы, выполнять действий над матрицами.
2. Литература:
2.1. В.А. Подольский "Сборник задач по математике" гл.3 §5,6 М.: Высшая школа, 1990 г.
2.2. Н.В. Богомолов "Практические занятия по математике" гл.4 §1 М.: Высшая школа, 1990 г.
3. Подготовка к работе:
3.1. Изучить теоретический материал по теме: «Определители и их свойства».
3.2. Подготовить бланк отчета
3.3. Подготовить ответы на вопросы допуска к работе:
3.3.1. Понятие определителя третьего порядка.
3.3.2. Методы вычисления определителя второго порядка.
3.3.3. Методы вычисления определителя третьего порядка.
3.3.4. Свойства определителей.
3.3.5. Понятие матрицы. Свойства матриц.
3.3.6. Понятие транспонированной, обратной, нулевой, симметричной матрицы.
3.3.7. Понятие минора элемента матрицы.
4. Основное оборудование:
4.1. Литература, конспект.
5. Задание:см. приложение.
6. Порядок выполнения работы:
6.1. Изучить теоретический материал.
6.2. Выполнить задание согласно варианту.
6.3. Выполнить дополнительные задания.
7. Содержание отчета:
7.1. Титульный лист.
7.2. Цель работы.
7.3. Условие, решение и ответ предложенного задания.
7.4. Ответы на контрольные вопросы.
8. Контрольные вопросы:
8.1. Понятие определителя третьего порядка.
8.2. Методы вычисления определителя второго порядка.
8.3. Методы вычисления определителя третьего порядка.
8.4. Свойства определителей.
8.5. Случай, когда определитель равен нулю.
8.6. Дать понятие матрицы. Свойства матриц.
8.7. Понятие транспонированной, обратной, нулевой, симметричной матрицы.
8.8. Вычисление обратной матрицы. Минор элемента матрицы.
9. Приложение:
9.1. Задания:
Вариант 1
1.Вычислить определители третьего порядка, применяя различные методы вычисления.
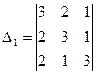
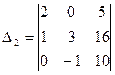
2. Найти
а) матрицу, транспонированную заданной матрице.
б) матрицу, обратную матрице А.
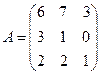
3. Вычислить разность матриц 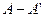 .
.
4. Вычислить произведение матриц 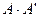 .
.
Вариант 2
1.Вычислить определители третьего порядка, применяя различные методы вычисления.
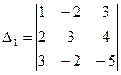
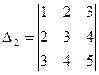
2. Найти
а) матрицу, транспонированную заданной матрице.
б) матрицу, обратную матрице А.
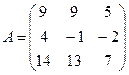
3. Вычислить разность матриц 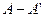 .
.
4. Вычислить произведение матриц 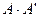 .
.
Вариант 3
1.Вычислить определители третьего порядка, применяя различные методы вычисления.
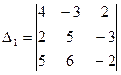
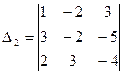
2. Найти
а) матрицу, транспонированную заданной матрице.
б) матрицу, обратную матрице А.
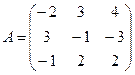
3. Вычислить разность матриц 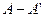 .
.
4. Вычислить произведение матриц 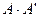 .
.
Вариант 4
1.Вычислить определители третьего порядка, применяя различные методы вычисления.
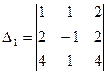
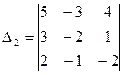
2. Найти
а) матрицу, транспонированную заданной матрице.
б) матрицу, обратную матрице А.
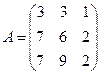
3. Вычислить разность матриц 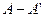 .
.
4. Вычислить произведение матриц 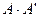 .
.
Вариант 5
1.Вычислить определители третьего порядка, применяя различные методы вычисления.
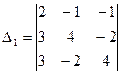
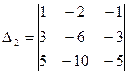
2. Найти
а) матрицу, транспонированную заданной матрице.
б) матрицу, обратную матрице А.
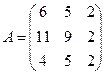
3. Вычислить разность матриц 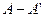 .
.
4. Вычислить произведение матриц 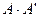 .
.
Вариант 6
1.Вычислить определители третьего порядка, применяя различные методы вычисления.
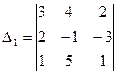
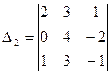
2. Найти
а) матрицу, транспонированную заданной матрице.
б) матрицу, обратную матрице А.
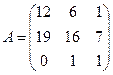
3. Вычислить разность матриц 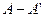 .
.
4. Вычислить произведение матриц 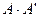 .
.
Методические указания.
Определителем первого порядка A = (a11) называется элемент a11:
∆1 = ׀ А׀ = a11.
Определителем второго порядка А =(aij) называют число, которое вычисляется по формуле:
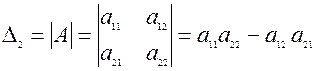
Произведения a11a22 и a12a21 называются членами определителя второго порядка.
Определителем третьего порядка A = (aij) называется число, которое вычисляется по формуле:
∆3 = ׀А׀ = a11a22a33 + a12a23a31 + a21a32a13 – a31a22a13 – a12a21a33 – a32a23a11.
Это число представляет алгебраическую сумму, состоящую из 6 слагаемых, или 6 членов определителя. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Знаки, с которыми члены определителя входят в формулу, легко запомнить, пользуясь схемой, которая называется правилом треугольников или правилом Сарруса.












 a11 a12 a13
a11 a12 a13
 | |||||
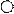 | 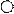 | ||||
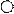 | 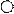 |






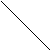
 a21 a22 a23
a21 a22 a23




 a31 a32 a33
a31 a32 a33
Минором Mij элемента aij матрицы n-го порядка называется определитель матрицы (n – 1)-го порядка, полученной из матрицы А вычеркиванием i-ой строки и j-го столбца.
Алгебраическим дополнением Aij элемента aij матрицы n-го порядка называется его минор, взятый со знаком (-1)i+j:
Aij = (-1)i+j Mij
Т.е. алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца (I + j) – нечетное число.
Теорема Лапласа.Определитель квадратной матрицы равен сумме произведений элементов любой строки ( столбца) на их алгебраические дополнения:
∆ = ai1Ai1 + ai2Ai2 + … + ainAin = 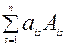
( разложение по элементам j-го столбца; j = 1,2, …, n).
