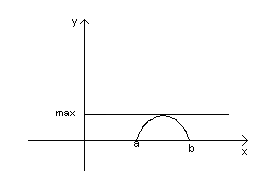
Геометрический смысл теоремы

В предположение теоремы всегда существует точка, в которой касательная к графику функции параллельная OX.

БИЛЕТ 31. Теорема Ролля.

Теорема Ролля:

Пусть функция y= :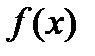

1) непрерывна на отрезке [a,b];

2) дифференцируема (a,b);

3) f(a)=f(b), тогда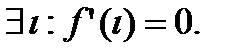

Доказательство.

Функция f(x), непрерывна на [a,b] достигает на нем max M и min m значения, т.е 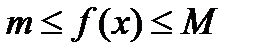. Возможны два случая.

1) 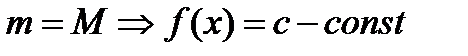и

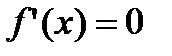
2) 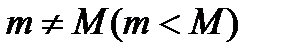,тогда либо максимальное значение f(x) либо минимальное значения f(x) достигается внутри интервала (a,b) (не на конце отрезка [a,b]).(f(a)=f(b)). 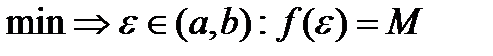, тогда 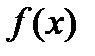достигает максимального или минимального значения во внутренней точке интервала (a,b) и по теореме Ферма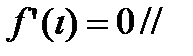

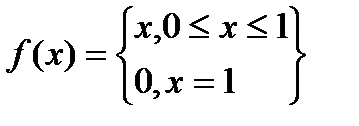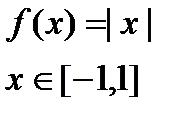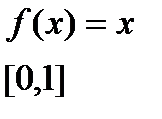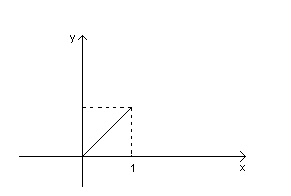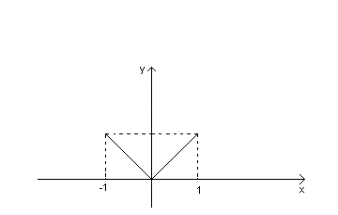Все условия теоремы Ролля существенные. Если выполняется, только 2 из 3(см. картинку), то не существует точка причем 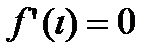(касательная параллельная оси ОХ).

БИЛЕТ 32. Теорема Лагранжа (формула конечных приращений).

Теорема Лагранжа.

Пусть функция f(x)

-непрерывна на отрезке [a,b];

-дифференцируема на интервале (a,b);

Тогда 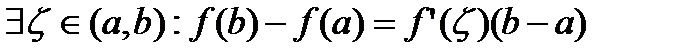(формула конечных приращений)

Доказательство.

Рассмотрим функцию 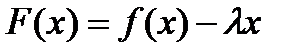.Параметр 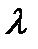выберем из условия F(a)=F(b)

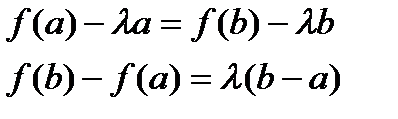
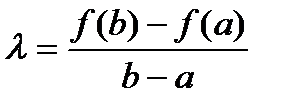
Функция F(x) удовлетворяет всем условием т.Ролля (она непрерывна и дифференцируема, как сумма непрерывных и дифференцируемых функций )

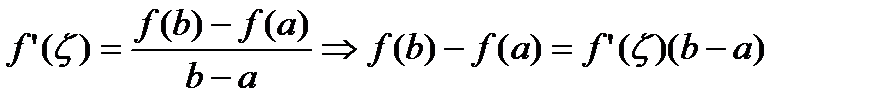
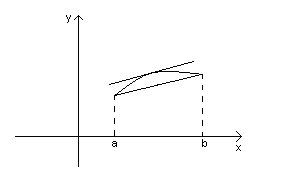
Геометрический смысл.

В предположение теоремы существует точка 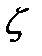:касательная к графику функции параллельна секущей(хорде).

Следствие.

Пусть f(x) определена, непрерывна и дифференцируема на (a,b). И в каждой точке интервала (a,b) 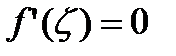, тогда f(x)=const.

Доказательство.

Пусть x1 и x2 две произвольные точки интервала(a,b),тогда 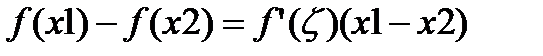, точка 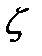лежит между этими точками x1 и x2, по условию 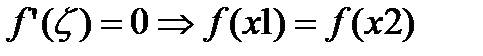, т.е f(x)=const(в силу произвольности выбора x1 и x2).

БИЛЕТ 33. Теорема Коши (обобщенная формула конечных приращений).

Теорема Коши.

Пусть функции 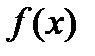и g(x) определены на интервале (a,b)

1) 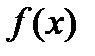и g(x) непрерывны на [a,b];

2) 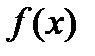и g(x) дифференцируемы на (a,b) причем 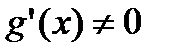, тогда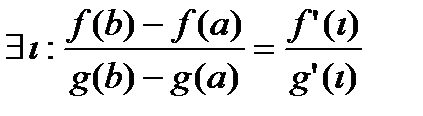

Доказательство.

Рассмотрим функцию 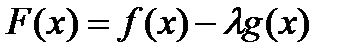параметр 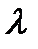выбрали из условия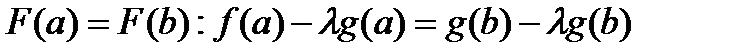

.

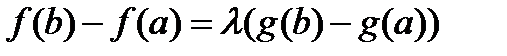
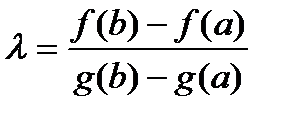Для функции F(x) выполнены условия теоремы Ролля. Формулировка теоремы Ролля 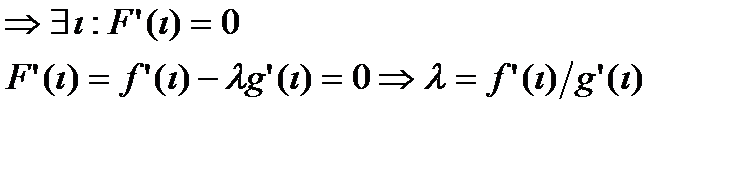Сравнивания формулы для 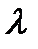, получим утверждение теоремы.

Следствие.

Теорема Лагранжа. Если 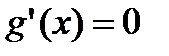,то .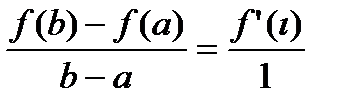

БИЛЕТ 34. Условие постоянства функции. Условие монотонности функции.

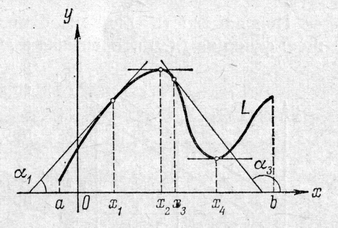
На рисунке нарисован график функции 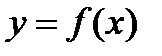, всюду имеющей производную. В точке 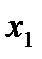касательная к 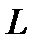и ось 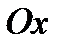образуют острый угол 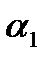, поэтому ее угловой коэффициент, равный 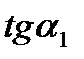, положителен. Но 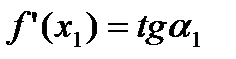. Следовательно, 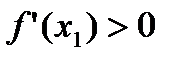. И так будет в любой точке интервала 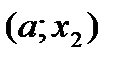, где функция 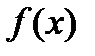монотонно возрастает. Напрашивается вывод: если на интервале , то на этом интервале функция монотонно возрастает. Далее, в точке 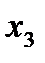касательная к 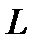образует с осью 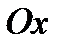тупой угол , поэтому ее угловой коэффициент, равный 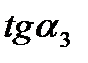отрицателен. А так как 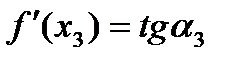, то 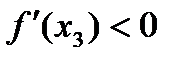. Вывод: если на интервале 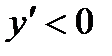, то на этом интервале функция монотонно убывает. В точке 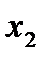функция имеет максимум. На чертеже ясно, что в этой точке касательная к параллельна оси , и поэтому ее угловой коэффициент равен нулю, так что 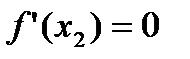. При этом слева от этой точки 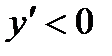, а справа .