Интерполяционный многочлен Ньютона
Пусть 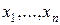 − набор узлов интерполирования,
− набор узлов интерполирования, 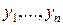 − значения функции
− значения функции 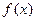 в узлах.
в узлах.
Величину 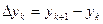 называют конечной разностью первого порядка в к-ом узле.
называют конечной разностью первого порядка в к-ом узле.
Аналогично определяются конечные разности высших порядков.
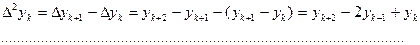
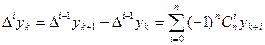 .
.
Разделенной разностью первого порядка называется выражение
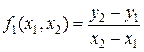 ,
,
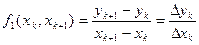 .
.
Разделенной разностью второго порядка называется выражение
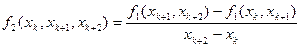 и т. д.
и т. д.
Используя представление функции f(x) в текущей точке x через разделенные разности можно показать, что
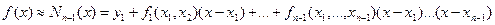 . (2.9)
. (2.9)
Очевидно, при 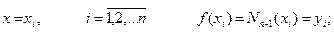
т. е. 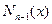 − интерполяционный многочлен. Его называют интерполяционным многочленом Ньютона.
− интерполяционный многочлен. Его называют интерполяционным многочленом Ньютона.
Рассмотрим случай равноотстоящих узлов, т. е. xi-xi-1=h
Тогда после нескольких преобразований получим:
интерполяционный многочлен Ньютона-Грегори:
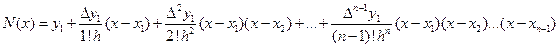 .
.
Пример:
Пусть требуется найти интерполяционный многочлен для функции 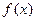 , имеющей в узлах
, имеющей в узлах 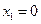 ,
, 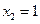 ,
, 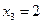 ,
, 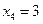
значения 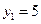 ,
, 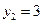 ,
, 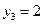 ,
, 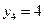 .
.
Шаг h=1,m=4.
Вычислим конечные разности:
| xi | 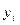 | 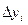 | 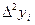 | 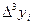 |
| 3 2 4 | -2 -1 2 | 3 |
N3(x)=5+-2/(1!*1)(x-0)+1/(2!*12)(x-0)(x-1)+2/(3!*13)(x-0)(x-1)(x-2)
Аналитический вид полинома Ньютона-Грегори третьего порядка:
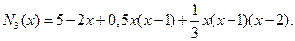
Варианты заданий
1. Во всех вариантах требуется аппроксимировать заданную исходную функцию f(x) многочленом Лагранжа на интервале [a, b], m - количество точек (узлов), в которых задана функция. Т.е. таблица исходной функции yi=f(xi) вычисляется в точках 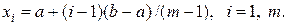
2. Используя полученную таблицу 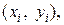 требуется вычислить значения функций
требуется вычислить значения функций 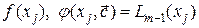 и погрешность
и погрешность 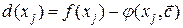 в точках
в точках 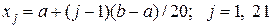
(в узловых точках d(xj=xi )=0)
Таблица 2.1
| N | Функция f(x) | а | В | m |
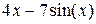 | -2 | |||
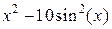 | ||||
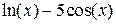 | ||||
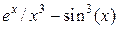 | ||||
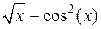 | ||||
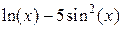 | ||||
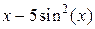 | ||||
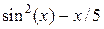 | ||||
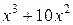 | -8 | |||
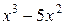 | -2 | |||
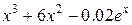 | -5 | |||
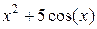 | -1 | |||
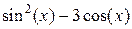 | ||||
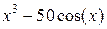 | -3 | |||
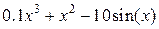 | -4 |
2. Для всех вариантов проведите линейную интерполяцию между двумя соседними узлами для десяти дополнительных промежуточных точек.
3. Используя исходную таблицу yi=f(xi) i=1,m, получите аналитический вид полинома Ньютона-Грегори Nm-1(x). Требуется вычислить значения функций 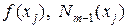 и погрешность
и погрешность 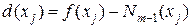 в точках
в точках 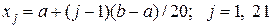
Можно только теоретически !!!
4. Постройте графики и проанализируйте качество полученной аппроксимации.
Контрольные вопросы
1. Как ставится задача линейной аппроксимации функций?
2. Что такое интерполяция, ее геометрическая интерпретация?
3. Напишите интерполяционный многочлен Ньютона 2-го порядка.
4. Напишите интерполяционный многочлен Лагранжа 2-го порядка.
5. Как получить формулу линейной интерполяции?
ЗАДАНИЕ 3. Алгоритмы численного интегрирования
Цель работы: изучить приемы составления алгоритмов и написания программ для вычисления определенных интегралов. Научиться вычислять определенные интегралы с заданной точностью.
