Линейные диф. Уравнения первого порядка
Задания, приводящие к диф. Уравнениям. Основные определения
Множество задач науки и техники. Например задача о вертикальном падении тела под действием сил тяжести и сопротивления среды.
R = kV, где – коэффициент пропорциональности, который определяется опытным путём и считается известным. Нужно найти закон изменения модуля скорости ( v=ϕ(t)) тела с течением времени (t). P= mg. m 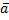 =
= 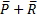 . Проецируя на ось Y получаем may=Py+Ry . Но ay= dVy /dt .
. Проецируя на ось Y получаем may=Py+Ry . Но ay= dVy /dt .
m dVy/ dt=mg-kV .
Дифференциальное уравнение – соотношение связывающее независимую переменную, функцию y=φ(x) и её производные 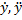 …. Если в диф. Уравнении функция зависит от одного аргумента, то такое уравнение называется обыкновенным дифференциальным уравнений.
…. Если в диф. Уравнении функция зависит от одного аргумента, то такое уравнение называется обыкновенным дифференциальным уравнений.
Порядок диф. Уравнения – наивысший порядок производной искомой функции.
Решение диф. Уравнения – всякая функция, подставляемая в уравнение и превращает его верное тождество. Например для 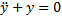 решением является y = sin(x).
решением является y = sin(x).
2. Геометрический смысл диф. Уравнения первого порядка.
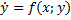
tgα = f(x,y) = 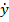
Дифференциальному уравнению на плоскости Oxy отвечает поле направлений . 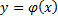 – решение диф. Уравнения. Направление касательной к кривой
– решение диф. Уравнения. Направление касательной к кривой 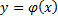 в её точке (x;y) совпадает с направлением поля в этой точке. В любой точке интегральной кривой направление касательной к ней совпадает с направлением поля в этой точке.
в её точке (x;y) совпадает с направлением поля в этой точке. В любой точке интегральной кривой направление касательной к ней совпадает с направлением поля в этой точке.
3. Диф. Уравнение с разделёнными и разделяющимися переменными.
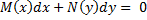
y = φ(x) – искомая функция от x, M(x), N(y) – заданные непрерывные коэффициенты аргументы относительно соответственно x и y.
По определению 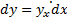 следовательно
следовательно 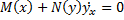 но диф. Уравнение первого порядка, следовательно и равносильное ему уравнение
но диф. Уравнение первого порядка, следовательно и равносильное ему уравнение 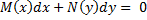 диф.уравнение первого порядка; такое уравнение называют диф. Уравнение с разделёнными переменными. Для его решения перейдём к
диф.уравнение первого порядка; такое уравнение называют диф. Уравнение с разделёнными переменными. Для его решения перейдём к 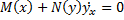 и возьмём неопределённый интеграл от обеих частей уравнения по x
и возьмём неопределённый интеграл от обеих частей уравнения по x 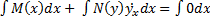 что равнозначно
что равнозначно 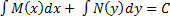 и придём к
и придём к
F1(x) + F2(y)= C получив общий интеграл уравнения. Таким образом, чтобы получить общий интеграл, в уравнении с разделёнными переменными нужно функцию M(x) проинтегрировать по x, функцию N(y) – по y и полученную сумму приравнять C.
4. Однородные диф. Уравнения первого порядка.
Однородное диф. Уравнение первого порядка – это диф. Уравнение первого порядка 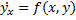 в которых правую часть f(x,y) можно представить в виде функции одного аргумента = y/x т.е. f(y/x) ,
в которых правую часть f(x,y) можно представить в виде функции одного аргумента = y/x т.е. f(y/x) ,
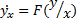 , F – непрерывная функция аргумента y/x
, F – непрерывная функция аргумента y/x
Представим y/x=U 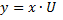 из этого вытекает что
из этого вытекает что 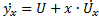
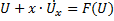
Представив это в виде 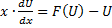 и умножив это на dx получаем диф. Уравнение с разделёнными переменными
и умножив это на dx получаем диф. Уравнение с разделёнными переменными 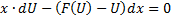 Решая его получаем
Решая его получаем 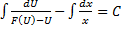
т.е. Ф(y/x) – ln(x) = C. При U(x)=U 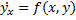 принимает вид
принимает вид 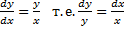 и после интегрирования имеем
и после интегрирования имеем 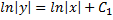 .
.
Итак y=C1x, при F(U)=U=y/x
Линейные диф. Уравнения первого порядка.
Линейные диф. Уравнения первого порядка это уравнения вида 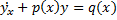
Где y=φ(x) – искомая функция , а p(x) и q(x) – заданные ,непрерывные на всё интервале x, функции от x. Введём две функции от x : U=U(x) , V=V(x) . И решение ищем через y=UV
Получаем 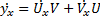 подставляя это в исходное уравнение получаем
подставляя это в исходное уравнение получаем
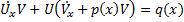 . Выберем функцию V(x) так ,чтобы сумма
. Выберем функцию V(x) так ,чтобы сумма 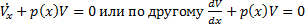 . Умножая на dx получаем уравнение с разделяющимися переменными dV+p(x)Vdx=0, решая его получаем
. Умножая на dx получаем уравнение с разделяющимися переменными dV+p(x)Vdx=0, решая его получаем 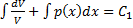
Примем произвольную постоянную C1=0 и получим 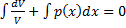 из чего получаем
из чего получаем
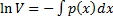 тогда V(x) =
тогда V(x) = 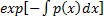 . Подставляя получимое в
. Подставляя получимое в 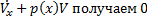 следовательно
следовательно 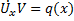
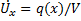 , после интегрирования получаем
, после интегрирования получаем 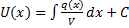 подставляем это в y=UV и имеем y =
подставляем это в y=UV и имеем y = 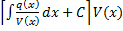 - решение исходного уравнения.
- решение исходного уравнения.
